


Next: Bibliography
Up: Transport Models
Previous: Guzdar-Drake Drift-Resistive Ballooning Model
For transport due to the kinetic ballooning mode, we compute 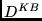 and
the thermal diffusivities in terms of the pressure gradient
and
the thermal diffusivities in terms of the pressure gradient 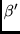 .
.
and where 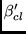 is the ideal pressure gradient threshold for
the onset of the ideal ballooning mode in
is the ideal pressure gradient threshold for
the onset of the ideal ballooning mode in 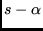 geometry,
geometry,
Here, 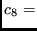 cswitch(8)=1 by default, but is included for flexibility.
The coefficent
cswitch(8)=1 by default, but is included for flexibility.
The coefficent 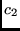 in the expression for
in the expression for 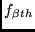 is set equal to
cswitch(2).
is set equal to
cswitch(2).
The diffusivities are then given as:
where 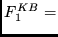 fkb(1),
fkb(1), 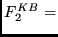 fkb(2),
fkb(2),
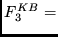 fkb(3), and
fkb(3), and 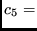 cswitch(5).
Note that the new version does not include
the (5/2) factor in the thermal diffusivities.
cswitch(5).
Note that the new version does not include
the (5/2) factor in the thermal diffusivities.
The relevant coding is:
transp_support
2001-12-21
![]() and
the thermal diffusivities in terms of the pressure gradient
and
the thermal diffusivities in terms of the pressure gradient ![]() .
.