Model with width based on flow shear stabilization

  This pedestal temperature model, which is given by Eq. (19) in Ref. [5], employs similar approach from section , but with different scaling of the width of the pedestal. The width of the pedestal, , is derived from the assumption that the suppression of long wavelength modes is assumed to be the relevant factor in establishing the edge transport barrier. The local growth of the long wavelength modes can be estimated by sound speed divided by the connection length between the bad curvature region, the destabilizing curvature region on the outer side of the torus, and the good curvature region, the stabilizing curvature region on the inner side of the torus, in the pedestal region. The following result for the pedestal width is obtained:
 
where is the gyro-radius, R is the major radius, q is the safety factor and C_W is a constant of proportionality chosen to optimize the agreement with experimental data.

After combining Eqs. ,  and  with some algebra, the following expression can be obtained for the pedestal temperature in the unit of keV:
 
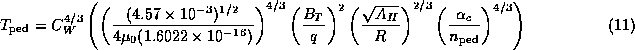
where A_H is the average hydrogenic ion mass in AMU and is the electron density at the top of the pedestal in units of m³. Note that Eq.  is a non linear equation as explained in section . The coefficient C_W in the expressions for the pedestal width [Eq. ()] and the pedestal temperature [Eq. ()] is determined by calibrating the model for the pedestal temperature against 533 data points for type I ELMy H-mode plasmas obtained from the International Pedestal Database version 3.1, using discharges from ASDEX-U, DIII-D, JET, and JT-60U tokamaks, as described in Ref. [5]. It is found that the value C_W = 0.22 yields a minimum logarithmic RMS deviation of about 30.8% for this data [5].