Status of studying Rosenbluth and Hinton's Neoclassical Rotation Issues in gyrofluid equations

Comments written by Greg Hammett May 27, 1997, with input from several others...

These are comments of work in progress for discussion among those involved. I am not completely confident that this is all correct...

To summarize the following:

1. At least for some initial conditions, the gyrofluid code appears to incorrectly damp the ExB flow to zero, instead of the residual value given by the Rosenbluth-Hinton formula and reproduced by Dimits' gyrokinetic code. However, for other initial conditions, the gyrofluid code does give a significant non-zero residual phi, but the scaling and dependence of this residual level is not yet clear.

2. The gyrofluid equations probably do have too much long-term damping of higher k_r rotation modes, due to an excessive neoclassical viscosity. I'm guessing the resulting damping rate scales like (v_t/R)*(k_r*rho)**2 (give or take factors of q or r/R perhaps). We have assumed that the short-term damping (of order v_t/R) and/or the turbulent viscosity exceeds this level, so that it doesn't matter much (see point 4 below). However, there could be regimes close to marginal stability where the turbulent viscosity isn't large enough to be dominant, and the excessive long-term neoclassical viscosity might reduce the rotation modes and cause us to overestimate chi. We could eventually try to quantify this criterion so we can quantify how close to marginal stability this occurs.

3. There are several approaches to fix these problems which we are looking into. One might be to adjust the existing Landau-fluid closure coefficients in various ways. [There is some freedom in the way these are chosen. The present coefficients were chosen to give a best fit to the toroidal response functions, but there are other possible coefficients which do not change the goodness of fit very much.] Another would be to explicitly add in some terms in the closures so that the Landau-damping causes the parallel heat fluxes to relax to their neoclassical values (a Pfirsch-Schluter heat flux analogous to the Pfirsch-Schluter flow). We are double checking the form of the Landau-damping operator (should |k_par| operate on q_par or on q_par/B, etc.)? Another approach would be to separate the ion gyrofluid eqs. into trapped and passing components and treat them separately (as Waltz has suggested). And another would be to treat the m=n=0 component with a fully-kinetic Vlasov treatment.

4. Even if the gyrofluid equations are getting the long-term behaviour of the m=n=0 rotation mode incorrectly, there are some reasons why the nonlinear chi might not change much. Nevertheless, we are taking this as a serious issue, because there is some chance that this causes the gyrofluid equations to overestimate chi. The planned GF/GK comparisons and additional diagnostics, which we are all pursuing, will be important.

There are several ways to look at point 4. Before going on with the details of point 1 above, let me go into more detail on point 4:

In the DIA treatment of turbulence, the turbulence generates both "nonlinear noise" which drives the amplitude of various modes and "nonlinear damping" which takes energy out of various modes. (Note that this is a "real" noise, i.e., treating part of the turbulence as a random source, as opposed to "particle noise", which is another topic...) For example, in regular Navier-Stokes turbulence, there is a wide "inertial range" of undamped modes, but their amplitude doesn't grow to infinity because the the nonlinear driving of them is balanced by the nonlinear damping of them. Rosenbluth and Hinton focussed on the turbulent "nonlinear noise" driving the linearly undamped m=n=0 modes, but there should also be nonlinear damping of these modes. Physically, this correponds to a turbulent viscosity which mixes regions of oppositely directed poloidal flow.

I believe there is some evidence for this in Dimits' gyrokinetic paper at the 1994 IAEA meeting (Vol. III, p. 457). In his Fig. 2 is a scan of chi vs. r/R. If Rosenbluth and Hinton's mechanism were dominant (that the turbulent viscosity is small and that larger r/R allows larger levels of the rotation mode to build up), then one would expect that chi would drop as r/R is increased from 0 to 0.2. However, Dimits found that in fact chi_hat increased from about 0.75 to 1 as r/R was increased from 0 to 0.2. This would be consistent with our general experience as well, that increasing r/R increases the trapped-ion drive of the turbulence some.

This suggests that r/R=0 is a useful GF/GK benchmark point, since then the rotation mode should damp completely to zero, eliminating any concerns about its possible long-term build up. Does the r/R scan from Dimits' 1994 IAEA paper need to be redone with the present version of his GK code before the GF code compares with it?

Further details:

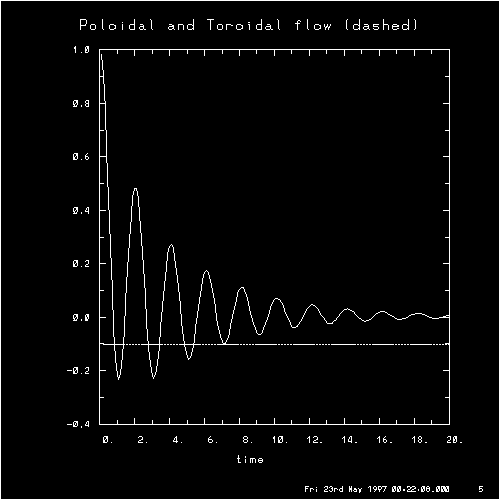This figure is my gyrofluid attempt to reproduce the lower graph in a figure by Dimits of the gyrokinetic response of a plasma to shield an externally imposed Phi. The parameters are the same as in Fig. 5.11(b) of Beer's thesis , i.e., q=1, eps = r/R=0.1, k_r*rho = 0.01. Time is normalized to units of L_n/v_ti (and L_n/R=1). Concentric circular flux surfaces are assumed. At t=0, an external Phi is imposed with Phi_ext=1/k_r*cos(k_r*r) (the factor of 1/k_r is so that that the resulting v_ExB will be 1). The solid (oscillatory) line is the resulting poloidal flow, and the dotted (constant) line is the toroidal flow. Toroidal momentum is properly conserved.

The difference between the ExB flow and the poloidal flow can be neglected for these parameters. Dimits' total phi is given by his imposed phi minus his response phi. The result can then be compared with the solid line in the gyrofluid curve above. Note that gyrofluid ExB flow is damping to approximately zero, so it looks like it is getting the wrong result for these parameters. In Dimits' figure the gyrofkinetic phi reaches a steady state level of about 15% of its initial value, consistent with the Rosenbluth-Hinton shielding factor I will define as S_RH:

S_RH = 0.6*eps**0.5/q**2 / (1 + 0.6*eps**0.5/q**2)

This is based on Dimits' interpretation of Eq. 9 of the earlier Rosenbluth-Hinton memo . [I have not gone through the algebra of the Rosenbluth-Hinton memo, but Dimits' interpretation seems to me to be intuitively correct. Attached is my view of a physical picture of the Rosenbluth-Hinton effects .] Both the gyrofluid and gyrokinetic phi(t) plots show oscillations due to the excitation of a "global acoustic mode" (a mode identified in a recent paper by Novakovskii, related to the ion acoustic wave and toroidal effects). As Novakovskii, shows, the damping of this mode is proportional to something like exp(-q**2), so for high q one would have to wait a long time for it to decay away. The gyrofluid code reproduces the real part of the frequency of this mode from the gyrokinetic simulation fairly well, but the gyrofluid damping rate appears to be about half of what it should be for this case.

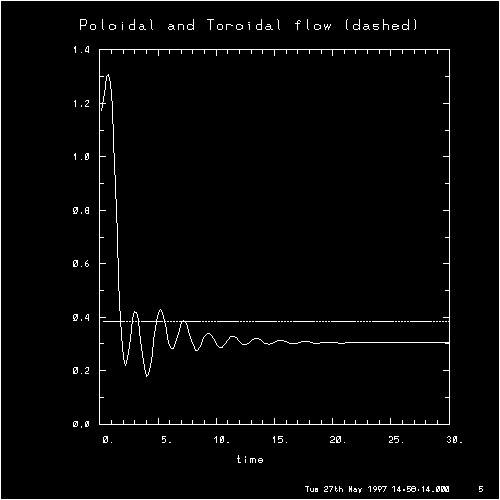This is an earlier case we had done, with q=1 and eps=r/R=0.3 to try to maximize the expected residual v_E, and indeed the gyrofluid code gives a significant residual level of v_E. One difference between this and the first case is that instead of just imposing an external phi, we initialized a density (and corresponding phi and v_E) and u_par perturbation of the form:

v_E = cos(k_r*r)

u_par = [ 1/(1+eps*cos(theta)) -2*q*cos(theta)/(1+eps*cos(theta)) ] * cos(k_r*r)

This was the default initializations used in the tests in Beer's thesis (caution: in Fig. 5.10 and Fig. 5.11 of his thesis, v_phi and v_theta are initialized to their initial values, which are slightly different than 1). The part of u_par proportional to q was chosen to try to minimize excitation of the global-acoustic mode, while the other part of u_par was chosen just to make it large and verify that toroidal momentum is well conserved. To separate out the final ExB flow v_E from the poloidal and toroidal flows in the above plots, use:

v_E = (v_theta - v_phi*eps/q)/sqrt(1+eps**2/q**2)

This gives a residual v_E relative to the initial v_E of v_E1/v_E0=0.17, within 30% of the Rosenbluth-Hinton prediction of 0.25. (In fact, if you continue the gyrofluid simulation for a much longer time, you will find that this v_E wasn't quite in steady state yet, and would eventually rise to be about 15% larger than the Rosenbluth-Hinton prediction. But I don't understand why such a long-time scale is required...)

I do not understand why this case gives a significant residual v_E while the first case does not. It would be useful to extend the Rosenbluth-Hinton calculation of a residual phi to this case where a finite u_par is included in the initial conditions.