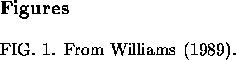Below we give a series of illustrations of accessing and combining information in the KB either already implemented in the current embryonic E3, or, for the later subsections, which experimentation to date indicates is feasible for the full system. This is interspersed with explanatory discussion.
In[1]:= energy[US,fossil,coal,1988]
Out[1]= 19.93 EJ,
In[2]:= area[US,cropland,1988]
6 2
Out[2]= 1.9 10 km
In[4]:= energy[NJ+NY,1988]/population[NJ+NY,1988]
-7
2.42483 10 EJ
Out[4]= --------------- .
cap
In[5]:= energy[US+Canada,fossil+nuclear,1988]
energy[Canada, fossil, 1988] not in KB.
energy[Canada, nuclear, 1988] not in KB.
Out[5]= 81.59 EJ + energy[Canada, fossil, 1988] + energy[Canada, nuclear, 1988]
In[6]:= ?EJ ; ?cap
An EJ is a unit of energy. Use SI[] to evaluate.
cap (capita) is the base unit of population, meaning one head.
In[8]:= SI[EJ]
18
Out[8]= 1. 10 Joule
In[9]:= convert[%4,kWh/cap]
67356.5 kWh
Out[9]= -----------
cap
In[10]:= SI[boardfoot]
3
Out[10]= 0.00235974 meter
In[11]:= SI[200 MW * 1 yr * .05 $US/kWh * .75]
7
Out[11]= 6.57 10 $US
In[12]:= ICC[BIG$ISTIG1]
770 $US
Out[12]= -------
kW
In[13]:= notes[BIG$ISTIG1]
Out[13]= noteA: Numbers for a biomass-fueled BIG/ISTIG system, with a \
> fixed-bed Lurgi gasifier without chemical hot-gas cleanup, and a 110\
> MW ISTIG unit.
In[14]:= energyDensity[poplar]
19.4 MJ
Out[14]= -------
kg
Here, the User's query and E3's response are on lines labeled with the standard Mathematica designation In[i] and Out[i], respectively (jointly referred to as [i] below).
In queries [1,2] are simple requests for 2 macro-numbers. To make matters as simple as possible for the User, E3 is fairly relaxed about the order of arguments, so that, for example, query [2] could also have been posed as area[1988,cropland,US]. In [4] is shown a query somewhat more involved than [1,2] in 2 ways: (a)one can combine the numbers for different regions such as New Jersey and New York by the summation designation in the argument, and (b)the numbers drawn from the KB can be combined in arbitrary algebraic combinations, such as the ratio energy[.]/population[.] shown there.
A more elaborate example of the summation syntax noted in (a) above is given in query [5], meaning `the sum of the fossil fuel plus nuclear energy used by the sum of the US and Canada in 1988.' Here, E3 finds that the KB knows the amount of fossil+nuclear energy the US consumed in 1988, but for Canada, it presently only knows the total amount of energy consumed. It therefore fails gracefully, giving the messages `energy[.] not in KB' for the items not known, and providing a symbolic result in the answer-line Out[5]. The given result is therefore still correct, though partly symbolic, and could be used in subsequent manipulations, or further evaluated by hand. This is one virtue of using a CAS like Mathematica over other computer languages or database query languages.
A first kind of support information is requested in [6],
the meaning of the symbols EJ and cap which were returned earlier.
The ?
symbol
notation is part of the help machinery
which Mathematica itself provides.
From [6] one learns that an EJ is an energy unit, whose value one can elicit as in [8] by calling the function SI[], which converts its argument to SI units ('Standard International'/MKS units, extended to units not encountered in physics, such as population, money, etc). In [9] a bit more general function convert[] is called, which uses SI[] to convert the result Out[4] (Mathematica shorthand %4) to kWh/capita.
These conversion functions should be a very useful, albeit simple, facility to have at one's fingertips, while absorbing the heterogeneous literature accessed in EE&E work, and where one regularly has to use and combine numbers in various, sometimes exotic units. Two typical examples are given in [10,11]. Query [11] is a one-line calculation answering the question[1] ``What would be the annual revenue of the envisioned ITER prototype fusion reactor if it produces 200 MW electric with a duty factor of 75%, and electricity sells at 5 cents/kWh?''
In [12], a first query for micro-numbers is made, the installed capital cost
(ICC) for a particular Biomass-fueled Integrated Gasification/
Intercooled Steam-Injected Gas Turbine (BIG/ISTIG) system,[2]
designated BIG$ISTIG1.
In the EE&E literature, a given technology is often characterized by a
table or two of its salient features, eg, its power output, conversion
efficiencies,
the costs of its components, and the busbar cost of electricity (COE) it
produces, as in Figure 
, drawn from 2 tables Ref. Wms8/89,
from which the numbers for BIG$ISTIG1 were taken.
Such information may be incorporated into the KB with much the same
organization as used for the macro-numbers. Similarly for micro-numbers
specifying the characteristics of materials, illustrated in [14].
The mature KB would contain the information in such tables for many
technologies and materials, and be able to access and make use of them.
In addition to the numbers exemplified in [12], good tables of this sort generally also have support information, notes on the assumptions in the numbers in the table. In [13] a simple method for eliciting this information is invoked. In the mature Apprentice, such messages could be automatically printed when a relevant number is accessed.
Help Facilities:
E3 will have online system-help capabilities, some simple illustrations of
which have just been given. These should permit the User to:
obtain a listing of the Apprentice functions available, and when
desired, a brief description of their usage,
find the meaning of system symbols not recognized by the User
(illustrated in [6,8] above), and conversely
get the system names for User-supplied expressions or
expression fragments. E.g.,
In[15]:= apropos[fuel cell]
Out[15]= {fuelCell,FCV}.
By using these utilities, the User should be able to find his way around the Apprentice system itself, clarifying the meaning of statements E3 makes, and to formulate statements he wants to make.
A second level of help is to enable the User to find his way around the knowledge the Apprentice holds. In addition to permitting E3 to effectively answer queries put to it, browsing this structure could provide a powerful pedagogic function, enabling a User to learn the structure of a given portion of the field.
Automating Economic Analysis:
A common task in EE&E work is assessing the economic
characteristics of a given system, once the numbers specifying the
system have been given. For example, the COE for BIG$ISTIG1 in
Figure b is computed from other information about BIG$ISTIG1, such
as its ICC (in Fig. a), its assumed capacity factor and lifetime,
and from more general economic relations and conventions for assessing the
cost of energy technologies, such as described in the
EPRI Technical Assessment Guide (TAG).
The Apprentice KB would include a knowledge
of these relations, and the mill would use these to compute such
derived quantities, asking the user to make further choices when
insufficient information has been given:
In[16]:= COE[BIG$ISTIG1]
E3: Specify discount rate (in percent):
>> 6.1
E3: Specify corporate tax rate (in percent):
>> 38
E3: Specify biomass[price] (in $US/GJ):
>> biomass[price]
$US (0.0179 + 0.00855 biomass[price])
Out[16]= -------------------------------------
kWh
Note that the User here leaves biomass[price] symbolic, so that the resultant expression can then be submitted to Mathematica's plotting routines, or further manipulated for use in subsequent tasks. In addition to eliminating tedium and potential for error, use of such routines could impose a more uniform framework on economic analyses.
Learning Capability:
Users will want to be able to add to and
customize the built-in KB (=KB0). A family of easy-to-use functions should
be constructed to permit them to do this, in a manner consistent
with the OO-organization of KB0. Among these should be functions
to define a new class-type (function defClass[]),
define a new object of that class (function defObj[]),
and view the present definition of a given object (function printObj[]).
For example, one could define a class `model' (see below) whose `slots'
are the sets of variables the model involves, and the sets of equations
governing those variables.
When experts in a given area have created increments dKB to KB0 in this fashion, their modules could be forwarded to a `KB-keeper', who could incorporate them into KB0. In this way, the extension of the KB could become a community effort, contributed to by experts in the various subdomains of the field.
Modeling:
A great deal can be learned from constructing and playing with relatively
simple mathematical models of EE&E issues (see, for example, Ref. Harte88).
These usually amount to systems of a modest number of algebraic and
ordinary differential equations, whose coefficients are of the sort
present in the KB described above.
Mathematica has built-in functions for
solving such systems. Thus, E3 could readily be given the capacity to
interactively construct, modify, and solve such models. A simple example
from Refs. Harte88,LSoltz96 governing rainfall, and so the amount
Mw of water in the global atmosphere is:
In[17]:= printObj[rainModel1]
object class: model
dynamic variables: {Mw}
parameters: {evap, Mw0, nu1}
equations:
odes:
{Mw'[t] == evap - precip[Mw[t]]}
algebraic eqns:
{precip[Mw_]:=If[Mw > 2 Mw0, nu1*Mw, 0] }
parametric values:
{evap=5.18 10^14 m^3/yr, Mw0=1.3 10^13 m^3}
Out[17]= rainModel1
Much of the information in the KB already discussed may be regarded as providing the parametric values describing natural, political, economic, and technological systems, each with specified input and output flows of energy, materials (input requirements, output products and byproducts), and money (governing the economics). Thus, models may be defined largely in terms of knowledge already in the KB, and may be composed into models of supersystems, using the OO framework for model definition, whose composite energy, material, and economic characteristics could thereby also be studied. Examples of such composite systems are Cavallo's scheme[5] for windfarms+compressed-air energy storage + transmission grid to provide baseload power to urban centers, or the interaction of the global climate with human activity modeled in PNL's MiniGCAM model[6] for projecting the impacts of different energy futures.
Accessing Information on the Web:
Today, an increasing amount of EE&E data are available on-line.
For example, the Web site www.wri.org maintained by the World Resources
Institute (WRI) contains about 162 pages of data tables containing current
information on environmental and resource conditions in over 150 countries.
We propose to extend the Apprentice to incorporate
access to the World Wide Web.
Our idea is to build into the Apprentice some of the features of Web browsers, but highly specialized for the EE&E domain. Mathematica has facilities for interacting with the outside software that will access the Web. The currently popular programming language Java has special features for Web access, and therefore is a suitable language for implementing the external software.
In the simplest case, the User could type in
In[18]:= webDisplay[worldLandArea&Use]
Out[18]= {}.
and the Apprentice would respond by accessing and displaying
Data Table 9.7 Land Area and Use from the site
www.wri.org. Here the knowledge of the various sources
of data contained in the system is a simple association between
Web pages and topics.
More interesting and useful is to extend this capability by allowing the User to enter a request for a specific piece of information and have the Apprentice retrieve the information from the appropriate Web page. For example (assuming for the purpose of this example that some sort of natural language capability has been implemented), a possible query and response is:
In[19]:= webQuery[``Percentage of land in Cameroon that is domesticated'']
Out[19]= {19%}
In this example the Apprentice has utilized its
knowledge of
which categories of EE&E related information can be found
on which Web pages to access the same
Data Table 9.7 from www.wri.org and pull out the percentage
of domesticated land in Cameroon.
These extensions would relieve the EE&E researcher/student from the tedium of searching through Web sites for information. Facilities could be developed so that if the User queries E3 for a piece of information that it doesn't have, it could automatically query its Web facilities for that piece of information. Additionally, it should be made easy for Users with the right privileges to add the result of the query to the EE&E\ database.
The possibility of incorporating agent-like capabilities raises a number of interesting research possibilities. For example, one could have a program/agent continuously monitor the internet and automatically notify the User if a page in one of the EE&E related sites changes. Another possibility is to automatically search the internet for additional sites that may have EE&E related information.
Automating Higher-Level Analysis:
More speculatively, we propose extending the core E3 discussed so far
with facilities for solving high-level queries, comparable to those addressed
in a typical paper or section of a paper in this area. For example,
Processing such a high-level query would result in the execution of a series of basic Mathematica commands with the output of each command appropriately gathered and processed. While seeming highly futuristic from the standpoint of numerical tools normally used in the EE&E domain, problem solving and planning tools developed by the AI community may be adaptable to handle such tasks.[7, 8]
The approach would be to develop a language for writing general high-level plans specifying the pieces of knowledge and tests that need to be performed to answer such questions. This is similar to an approach that has been taken in the context of AI robotic planning methods [7]. This general plan would then be expanded into a complete plan (i.e., a correct series of lower-level E3 commands) by utilizing tools and techniques available in the AI literature on planning [8].
The facilities described here would
enable a user without a detailed knowledge of Mathematica
or E3 to address some relatively involved problems.
The results of such problem solving would doubtless sometimes
ignore factors a human would consider essential, and would thus
have to be subjected to human reality checks. But it could
provide a good means of generating raw answers to questions
which would then be refined by human interaction, of
bringing out previously unrecognized assumptions in existing thought
on an issue, and might provide novel approaches to viewing
a problem.
References
