center
for extended magnetohydrodynamic modeling
A Proposal referencing Program Announcement LAB01-10
Scientific Discovery through Advanced
Computing:
Advanced Computational Research in Fusion Science
Office of Fusion Energy Science
U. S. Department of Energy
15 March 2001
Principal
Investigator: Laboratory
Official:
Stephen C. Jardin Rich
Hawryluk
Principal Research Physicist Deputy
Director
Princeton Plasma Physics
Laboratory Princeton
Plasma Physics Laboratory
609 243-2635 (voice) -2662 (fax) 609
243-3306 (voice) –2749 (fax)
email: jardin@pppl.gov email:
rhawryluk@pppl.gov
- - - - - - - -
- - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - -
Requested Funding : FY 2001: $1,000,000
FY 2002: $1,147,000
FY 2003: $1,222,000
Co-PIs and Senior Personnel:
PPPL: Guoyong Fu, Wonchull
Park SAIC: Scott
Kruger, Dalton Schnack
MIT: Linda E.
Sugiyama LANL: Rick
Nebel
NYU: Hank
Strauss U. Colorado: Scott
Parker
General
Atomics: Dave Schissel Utah State U.: Eric Held
U.
Texas (IFS):
Frank Waelbroeck
U.
Wisc: Jim Callen, Chris Hegna, Carl Sovinec
Note: Institutional contacts underlined.
No human subjects or vertebrate animals are to be used in this project.
Table of Contents
Abstract 3
Narrative
Background and
Significance 4
Preliminary Studies 7
Research Design and
Methods 15
Subcontract or
Consortium Arrangements 28
Literature Cited 29
Budget and Budget Explanation 31
Other Support of Investigators 33
Biographical Sketches 34
Description of Facilities and Resources 38
Appendix A: Plasma Fluid Models 39
Appendix B: Collaboration Letters 41
Appendix C: The Software
Framework
Appendix D: Institutional Budget
Pages
Appendix E: Deployment Tables
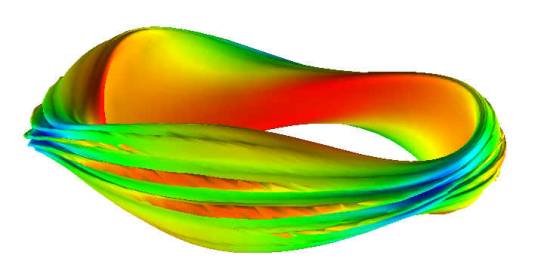
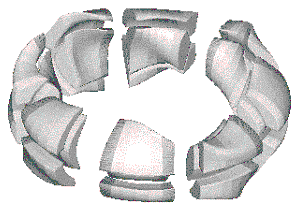
Figure 1:
3D MHD simulation shows that a toroidally localized ballooning mode develops in
the LI383 stellarator design when the design beta limit is exceeded. The equi-pressure surface reveals the mode
steepening nonlinearly to form ribbon-like structures. The color represents a particular flux
variable. [M3D calculation by Strauss and Park]
- Abstract -
The proposed Center for Extended Magnetohydrodynamic Modeling will enable a realistic assessment of the mechanisms leading to disruptive and other stability limits in the present and next generation of fusion devices. The main work involves extending and improving the realism of the leading 3D nonlinear magneto-fluid based models of hot, magnetized fusion plasmas, increasing their efficiency, and using this improved capability to pioneer new tera-scale simulations of unprecedented realism and resolution. This will provide new insights into some of the most critical and complex phenomena in plasma and fusion science. The proposed work builds on the established research teams that have developed the NIMROD and M3D codes. Activities are proposed in the following areas: Code Development -- improving the computational performance, implementing extended MHD models, and validation of the numerical algorithms; Model Development -- refining numerically tractable physical models for extended MHD (XMHD) and testing their efficacy; Visualization and Data Management -- providing visualization and data handling capabilities; Computer Science Enabling Technologies (CSET) -- which consists of several supporting computer science projects; Code Support, consisting of disseminating the code capability to the community, and supporting the developing user base; Applications and Validation – applying and validating the underlying models through cross-code and experimental comparisons.
1. Background and Significance
1.1 Overview
The proposed Center for Extended Magnetohydrodynamic Modeling (CEMM) will develop and deploy predictive computational models for the study of low frequency, long wavelength fluid-like dynamics in the diverse geometries of modern magnetic fusion devices. These models will be used to extend our fundamental scientific knowledge of the nonlinear dynamics of hot, magnetized plasmas. This will further the programmatic aims of the magnetic fusion energy program by providing fundamental insight into the processes that cause plasmas to undergo spontaneous transitions from states that are stable and confined to ones that are unstable and disruptive, or that exhibit poor plasma confinement.
The proposed Center consists of three central elements: existing and evolving large-scale simulation codes, theoretical model development, and state-of-the-art computer science support for algorithmic solvers, visualization, and data management. The first CEMM element brings together the two established computational research teams that have developed the NIMROD and M3D codes, and whose members have considerable experience in the development and application of plasma fluid models. Each of these major codes has demonstrated scalable performance on present massively parallel architectures, and both codes are ready to take advantage of new supercomputer technology as it emerges. The theoretical CEMM element will seek to elucidate the extensions to the resistive MHD model that are required to describe the dynamics of modern fusion plasmas. We call these extended models “extended MHD” or “XMHD”. Unlike independent theory, this effort will focus on casting the resulting equations in a computationally efficient form for implementation. The supporting computer science CEMM element will emphasize the development and implementation of mesh generators, discretization packages, linear algebra algorithms, specialized visualization tools, and data base structures that improve the code efficiency and enhance the manipulation and analysis of the resulting data. Rather than being located at a particular institution, the proposed CEMM will be an inter-disciplinary, multi-institutional team. This facilitates obtaining the required technical expertise from the appropriate places both within and outside the existing fusion program. The majority of our team has collaborated successfully under the Office of Fusion Energy Science PSACI pilot project; we have experience in such a distributed technical effort.
The Center has made a conscious decision to retain two code lines, M3D and NIMROD. The details of these codes are described in Section 2.3. These codes overlap considerably in their capabilities; the fact that they have been developed separately and use very different numerical representations allows them to serve as essential independent checks on one another. They also have their own unique strengths. The NIMROD code utilizes a Fourier representation in the toroidal angle and emphasizes the development of strongly implicit, highly parallel computational schemes. The M3D code uses a 3D mesh and a real space representation. It is better suited to problems with inherently three dimensional boundaries such as stellarators. Recent developments enable these codes to share data storage and visualization systems and software. These developments, achieved through the PSACI pilot project, will be extended in the CEMM to include the sharing of physical models and numerical methods.
Details of the proposed Center for Extended MHD Modeling are given in the body of this proposal. The remainder of Section 1 provides the programmatic motivation for the establishment of the CEMM, and it describes the compelling scientific challenge to be addressed by the Center. Section 2 contains: detailed background information, including discussions of the difficulty of the physics problem at hand, the formidable computational obstacles that must be overcome, and the present status and capabilities for the simulation of extended MHD. The specific technical approach of the proposed effort is given in Section 3. A brief description of several targeted application problems is given in Section 4. A detailed management plan is presented in Section 5.
1.2 Programmatic Motivation
The magnetic fusion program is presently embarked on two major development paths. One is to explore the physics of burning (fusing) plasmas. The other is to investigate the basic plasma confinement properties of a wide variety of innovative fusion reactor concepts. A large component of the estimated costs of both development paths is caused by the uncertainty in the dynamical behavior of the plasma. Under some operating conditions, an experiment can spontaneously transform from a stable system exhibiting good confinement into one that exhibits poor confinement or becomes unstable and disruptive. The responsible physical phenomena are: usually long wavelength and nonlinear, characterized by extreme anisotropy in their spatial structure, and can evolve on time-scales that are much longer than the Alfvén wave transit time. Very little of predictive value is known about them, particularly their nonlinear behavior. Because of budget realities, few experiments can be built to investigate even the key physical phenomena. Therefore, the critical physics issues and designs for each development path must be precisely identified before funds are committed to construction and operation. This requires increasing our knowledge and predictive ability of the critical nonlinear physics phenomena.
Numerical simulation can provide a key component of this effort, since computations are performed at a tiny fraction of the cost of an experiment. However, the computations must solve a physical model that accurately reproduces and predicts laboratory results. To be effective, the simulations must be combined with a well-focused, well-diagnosed experimental physics program to guide model development, and to assure the validity of numerical results. Recent developments in plasma theory, computational physics, and computer science, along with anticipated advances in computer hardware performance, combine to make this simulation capability a very attractive option in the near future. Developing and deploying this capability will be the focus of the CEMM.
1.3 The Scientific Challenge
The low frequency, long wavelength dynamics of hot, magnetized plasmas are not well understood for two reasons:
- Theoretical: The only practical means of describing low frequency global motions in real geometry is with a predominantly fluid model. The traditional magneto-hydrodynamic model (MHD) provides a good description of ideal and almost-ideal instabilities. A key challenge for present-day fusion research, however, is to predict and control instabilities that have much slower growth (see applications Sec. 3.5) but that dominate most experimental discharges. For slow modes, effects that are omitted in the MHD model due to finite Larmor radius, pressure anisotropy, and some long mean-free-path effects, become important. The theoretical challenge is to extend the standard MHD model to include the relevant effects while preserving computability.
· Computational: The physics problems that are important to fusion science are among the most daunting problems in computational physics. Macroscopic evolution of the confining magnetic fields can occur over time-scales that are orders of magnitude longer than those of the normal modes of the MHD model. Extended MHD introduces two-fluid modes and particle streaming at time-scales that are yet orders of magnitude faster than that of the MHD modes. Furthermore, both spatial structure and dynamics are fundamentally different perpendicular and parallel to the magnetic field. These properties of extreme separation of time and spatial scales, and extreme anisotropy combine to present a difficult computational challenge—one that is at least as difficult and scientifically compelling as the computation of fluid turbulence.
1.4 Proposed Center for Extended Magnetohydrodynamic Modeling (CEMM)
The programmatic need for a predictive simulation capability, and the theoretical and computational challenges involved in its development and deployment, combine to make a compelling case for bringing our best computational, theoretical, and computer science capabilities to bear on this problem. To this end, we propose the establishment of the Center for Extended MHD Modeling (CEMM). The Center will be interdisciplinary and multi-institutional, and will draw on expertise from both within and outside the present fusion science program. The Center will have six important components that will collectively enable the new Terascale applications:
· Advanced, parallel, scalable code development building on the strengths of the NIMROD and M3D codes;
· A synergistic theoretical and computational model development effort to distill the essential physics from the kinetic plasma description and to elucidate computationally efficient extensions of the appropriate fluid equations.
· The development of advanced visualization techniques and data base management for the efficient display and analysis of the four dimensional data produced by the computational models and to facilitate comparisons between NIMROD and M3D simulation results and experimental data.
· A computer science enabling technologies (CSET) program to implement specialized numerical algorithms and simulation components to improve the efficiency of the computational models, and to help manage code complexity and reduce development time.
· A code support effort to effectively disseminate these computational models to the fusion and general science communities.
· An aggressive applications and validation effort to compare the results of the two codes NIMROD and M3D: with one another, with analytic limiting cases, and with experimental data—the ultimate test;
Present budgets no longer allow the luxury of assembling such a group at a single institution. Instead, CEMM will be assembled from the staffs of many diverse institutions that participate in the fusion and computer science programs. (Note that the “pure” theory and experimental efforts will be funded out of the mainline OFES theory and experimental programs, and not from SCIDAC. We include them here because they are an integral part of the program. Similarly the majority of the CSET effort is funded separately as discussed in Sec. 3.4)
2. Preliminary Studies
2.1 Experimental Observations in Hot Fusion Plasmas
 Modern
fusion plasma experiments are rich in low frequency, long-wavelength electromagnetic,
i.e. MHD-like, activity. An example is
discharge number #86144 from the DIII-D experiment at General Atomics
Corporation in San Diego. This hot
plasma has a Lundquist number S (the ratio of resistive diffusion time to
Alfvén wave transit time) of about 108 and a magnetic Prandtl number Pr (the
ratio of the resistive diffusion time to the perpendicular viscous diffusion time)
of about 100. This discharge illustrates
much of the important nonlinear physics alluded to in Section 1.2 that will be
addressed by this proposal.
Modern
fusion plasma experiments are rich in low frequency, long-wavelength electromagnetic,
i.e. MHD-like, activity. An example is
discharge number #86144 from the DIII-D experiment at General Atomics
Corporation in San Diego. This hot
plasma has a Lundquist number S (the ratio of resistive diffusion time to
Alfvén wave transit time) of about 108 and a magnetic Prandtl number Pr (the
ratio of the resistive diffusion time to the perpendicular viscous diffusion time)
of about 100. This discharge illustrates
much of the important nonlinear physics alluded to in Section 1.2 that will be
addressed by this proposal.
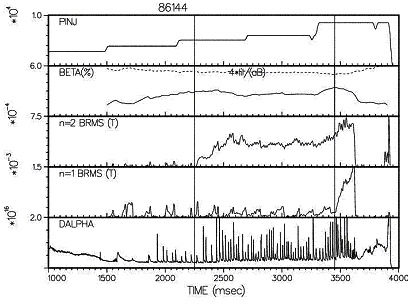
 Time traces of several experimental
diagnostics are shown in Figure 2. The top trace shows power injected from a
beam of energetic particles. The second
trace shows a normalized measure (b) of
the internal energy. The third and
fourth traces show two different toroidal harmonics (n = 2 and
n = 1) of the helical perturbations in the magnetic field. The bottom trace is a spectroscopic
diagnostic that responds to activity at the edge of the plasma.
Time traces of several experimental
diagnostics are shown in Figure 2. The top trace shows power injected from a
beam of energetic particles. The second
trace shows a normalized measure (b) of
the internal energy. The third and
fourth traces show two different toroidal harmonics (n = 2 and
n = 1) of the helical perturbations in the magnetic field. The bottom trace is a spectroscopic
diagnostic that responds to activity at the edge of the plasma.
For the first 2250 milliseconds (ms) of the discharge, the plasma internal energy increases in response to the energy injected by the neutral beam. The plasma also exhibits quasi-periodic oscillations in the n = 1 magnetic signal (called sawtooth oscillations). During this phase, the discharge is a steady state system with good plasma confinement. After 2250 ms things change dramatically. An n = 2 magnetic perturbation appears and grows to large amplitude, while the n = 1 oscillations continue unabated. The internal plasma energy now fails to increase in response to increases in the injected neutral beam power, and the edge D-alpha fluctuations occur much more frequently. The growth of an n=2 magnetic perturbation has been identified as a neoclassical tearing mode instability. At 3450 ms the disappearance of the magnetic signals indicates that the large, primarily n = 1, perturbations have "locked" to the wall of the device. A sudden and premature termination of the discharge quickly follows at 3900 ms. The confinement properties of the plasma have obviously been drastically altered by the events that began at 2250 ms. The phenomenology of these events and their evolution are not well understood.
Nonlinear simulations with the NIMROD code using conventional resistive MHD did not reproduce the salient features of the discharge [Gianakon99], even with dimensionless parameters approaching those of the experiment. Subsequent analysis determined that extended MHD physics underlies much of the dynamics. Successful comprehensive simulation of experiments such as DIII-D #86144 requires simultaneous modeling of
· realistic geometry to accurately capture the global nature of important macroscopic modes,
· high S and low viscosity conditions to ensure adequate separation of temporal and spatial scales,
· the ability to perform long time-scale simulations to follow the nonlinear evolution of the equilibrium configuration,
· realistic edge and boundary conditions, including a vacuum region, a moving plasma boundary, and a resistive wall to follow edge fluctuations and diffusion of magnetic perturbations into the wall,
· anisotropic heat flux and finite gyro-radius and banana-width effects to capture the nonlinear neoclassical island-size threshold,
· two-fluid effects for drifts and electron-physics modifications to global modes,
· kinetic extensions to reproduce free-streaming effects, and
· energetic particle effects to capture the growth rate modification of the sawtooth oscillation.
Considerable progress has already been made by the NIMROD and M3D teams in several of these areas. The objective of the proposed Center for Extended MHD Modeling (CEMM) is to bring all of these components together, to obtain a fundamental understanding of the nonlinear physics that limits performance in the most advanced fusion experiments.
2.2 Physics Background
Here we discuss the present status of the plasma simulation models referenced in this proposal, and give an overview of the physical effects to be addressed.
2.2.1 Plasma Models
Plasma dynamics are completely described by the evolution of
the distribution function ![]() , for each particle species a as given by an
appropriate plasma kinetic equation of the form
, for each particle species a as given by an
appropriate plasma kinetic equation of the form ![]() , where
, where ![]() is a complicated collision
operator describing collisions between species a
and b. This kinetic equation must be solved consistently
with the evolution of the electric and magnetic fields, using Maxwell’s equations. For applications to real plasmas, this evolution
must be obtained in a realistic experimental geometry. In general, such a full kinetic
electromagnetic description is both analytically impossible and
computationally impractical.
is a complicated collision
operator describing collisions between species a
and b. This kinetic equation must be solved consistently
with the evolution of the electric and magnetic fields, using Maxwell’s equations. For applications to real plasmas, this evolution
must be obtained in a realistic experimental geometry. In general, such a full kinetic
electromagnetic description is both analytically impossible and
computationally impractical.
There are two general categories of three-dimensional plasma simulations in current use: resistive MHD and electrostatic turbulence. The first category, resistive MHD (or often just called MHD), uses the model given in Appendix A as Eq. (A1a-f) with a single scalar pressure (i.e., P = 0). This is a common and useful approximation that is only strictly valid for plasma motions at the Alfvén velocity and in the high collisionality and small gyroradius limit. These assumptions are not satisfied in fusion plasmas; thus we can expect the MHD model to give at best only qualitative results. The second category of simulations, electrostatic turbulence, treats the ions using a gyrokinetic (or gyro-Landau-fluid) description; but it assumes that the magnetic field is static and that the electrons respond adiabatically. This model is useful for studying short spatial scale turbulence that is responsible for most anomalous transport in fusion devices; but is not useful for studying global “MHD” phenomena that require a full treatment of the magnetic field. [Note: Activity is underway in the electrostatic turbulence category to partially remove some of these restrictions. However, current work focuses on modeling fine scale dominantly electrostatic turbulent transport].
The thrust of the present proposal is to extend the resistive MHD category by addressing a more complex set of equations. The resultant extended MHD models will generically be denoted “XMHD”. These extended models lead to simulations that are improved in two ways. The first improvement is quantitative: the simulated plasma motion and growth rates for MHD dominant modes should be in better agreement with the experimental values. A more fundamental improvement, however is qualitative: XMHD simulations will be able to model entirely new classes of plasma phenomena.
The XMHD models discussed in this proposal fall into two general categories that will be discussed further in the next two sections. They are:
Two-fluid XMHD models with fluid-like equations for the electrons and the ions where the difference in their relative velocity and the anisotropy of the pressure tensor are accounted for, and
Hybrid particle/fluid XMHD models with numerically obtained closure relations where some or all of the ion response is obtained from particle solutions of the gyrokinetic equations and the electron response is obtained from fluid-like numerical solutions of the reduced phase space drift-kinetic equation.
Generally, the two-fluid XMHD models are less computationally demanding, but the hybrid XMHD models contain additional physical effects such as nonlinear wave-particle resonance that may be essential in certain classes of macroscopic phenomena. Note that the two models can have overlapping regions of validity; in particular they do if the nonlinear wave-particle resonance is not essential for the phenomena being modeled.
2.2.2 Two-fluid XMHD models
The general form of the two-fluid XMHD model is given in Appendix A as Eqs. (A-1a)-(A-1f), supplemented by Eqs. (A-2) and (A-3). The theoretical challenge is to define the ion and electron stress tensors Pi and Pe and the heat fluxes qi and qe. These terms contain a hierarchy of nonlocal effects, including finite (ion) Larmor radius (FLR) affects (which lead to gyroviscosity) and the effect of long collision lengths parallel to the magnetic field, including magnetic particle trapping (important in neoclassical effects). In the methods we have implemented to date [Sugiyama00, Gianakon96], the neoclassical parallel viscosity terms involving Pi and Pe are approximated using analytic neoclassical closures due to [Hirshman81] and [Callen86], and the ion gyroviscous contribution to Ñ· Pi uses approximations due to [Hazeltine92]. This latter expression is approximate for use in a nonlinear torus, since it assumes a uniform straight magnetic field and a small perturbation from an axisymmetric equilibrium.
2.2.3 Hybrid particle/fluid XMHD models
To model the nonlinear interaction of ions with MHD waves and to include large gyro-orbit and neoclassical effects more self-consistently, we have developed several hybrid methods, where either an energetic ion component or the whole ion population are modeled using the gyrokinetic or drift kinetic equations. In the methods implemented so far [Belova98], the ion fluid velocity is calculated by solving the momentum equation, and the calculated ion fluid velocity is used in the Ohm’s law, assuming quasineutrality. The ion pressure tensor is taken to be in the CGL (Chew, Goldberger, Lowe) form and the gyroviscous part of the stress tensor is calculated from the particles. Hot particle populations, for example fusion-produced a-particles or injected neutral beam ions, can be simulated by combining a gyrokinetic hot particle population with a fluid model for the background. [Park92]
The electron response is traditionally simulated using a fluid response. The proposed research will remove this restriction by further developing a Chapman-Enskog —like procedure for numerically solving the electron drift-kinetic equation [Held01]. This will allow a combination of neoclassical effects and parallel heat conduction effects to be properly modeled in low collisionality, long collision length hot fusion plasmas.
2.2.4 Physical Effects Introduced by Extended MHD
XMHD contains many effects that are absent from standard MHD and important in fusion plasmas.
Drift Waves: Two-fluid effects introduce electron and ion diamagnetic flows and hence drift wave effects into the MHD model. These can have important stabilizing or destabilizing consequences for plasma instabilities. For example, drift wave modifications are important in stabilizing high mode number resistive-MHD-type instabilities in hot fusion plasmas [Diamond86]. Such drift waves propagate radially away from their mode-rational surfaces, but are damped by kinetic processes such as ion Landau damping that limit the extent of their effects. An appropriate ion closure relation [Hendrick92] should be included in the model. It has also been hypothesized that nonlinear effects due to the ion diamagnetic drift can explain the observed stabilization of the internal, nearly-ideal MHD modes that cause sawteeth [Zakharov92].
Plasma Rotation. Extended MHD effects can cause changes in plasma equilibria and their response to rotation. The ions and electrons respond differently to rotational forces, due to their different masses; this generates a radial electric field that may persist in steady state [Bowers71]. In an axisymmetric system, neoclassical dissipation (the ion parallel viscous stress tensor) damps the plasma poloidal momentum. The dynamic effects become important when rotational forces exist. In addition, instabilities experience these effects. Growing magnetic islands rotate poloidally, leading to different self-consistent stabilizing or destabilizing effects.
Viscous Stress Tensor Effects: The higher order moments can drive new
instabilities. For example, the
appearance of ![]() in Ohm’s law,
Equation (A-1f), indicates that there is an electric field driven by the
divergence of the stress tensor. This
electric field drives a current parallel to the magnetic field, called the
bootstrap current, that is proportional to the pressure gradient perpendicular
to the magnetic field. This bootstrap
current exists independent from the applied electric field. These “neoclassical” effects can lead to
important macroscopic behavior known as neoclassical tearing modes
[Chang95] that are thought to set the pressure limits in many long-duration
tokamaks discharges and are not described by the resistive MHD model.
in Ohm’s law,
Equation (A-1f), indicates that there is an electric field driven by the
divergence of the stress tensor. This
electric field drives a current parallel to the magnetic field, called the
bootstrap current, that is proportional to the pressure gradient perpendicular
to the magnetic field. This bootstrap
current exists independent from the applied electric field. These “neoclassical” effects can lead to
important macroscopic behavior known as neoclassical tearing modes
[Chang95] that are thought to set the pressure limits in many long-duration
tokamaks discharges and are not described by the resistive MHD model.
Energetic Ion Component: In high temperature plasmas with a strong energetic ion component (such as in TFTR or JET), internal MHD modes, i.e., sawteeth, have been observed to be stable for extended periods. The net effect of hot particles may be stabilizing or destabilizing, depending upon their relative contributions to the total plasma beta (destabilizing) or the stabilizing kinetic term. There are other important kinetic effects involving the interaction of non-Maxwellian hot-ion particle populations with MHD modes. Among the most studied are the fishbone modes and the fishbone-like modes [Coppi00]. Fast ions can also destabilize toroidal Alfvén eigenmodes (TAEs), a stable normal mode of the ideal MHD spectrum in a torus [Cheng84].
These and other new physical effects contained in the XMHD equations can profoundly affect the dynamics of modern fusion plasmas. Specific applications to be addressed by CEMM are discussed in Section 3.5.
2.3 Computational Background
The CEMM is bringing to this project the two major 3D scalable fluid codes in the U.S. fusion program, NIMROD and M3D. These codes provide the framework within which the extensions in model capability and algorithmic efficiency will occur. This section describes the present status of these two codes and makes some observations on computational requirements for the future.
2.3.1
The NIMROD Code
The NIMROD code [Glasser99] solves the primitive form of the plasma fluid-model equations (A1-3) in axisymmetric toroidal, cylindrical, or periodic-linear geometry with arbitrary poloidal cross-sectional shape. (The geometry must have an ignorable periodic coordinate, but the simulated dynamics are fully three-dimensional.) The user selects which terms are retained in Ohm’s law, Equation (A-2), through an input parameter. The semi-implicit numerical method [Schnack87] is used to advance the solution from initial conditions. This avoids severe time step restrictions associated with wave-like normal modes of the system, sound, Alfvén, and whistler waves—while avoiding numerical dissipation. For accuracy at time steps that are orders of magnitude larger than explicit stability limits, the semi-implicit operator for mass motions is based on the linearized ideal MHD energy integral [Lerbinger91]. Matrix inversion is accomplished by parallel preconditioned Krylov methods, which is the most computationally demanding part of the time advance. Performance is therefore dependent on the effectiveness of the preconditioner [Plimpton99].
 The spatial representation of NIMROD is an
important feature of the code. NIMROD
uses a combination of logically quadrilateral and triangular finite elements
for the poloidal plane and pseudospectral collocation for the periodic
direction [Orszag71]. The
The spatial representation of NIMROD is an
important feature of the code. NIMROD
uses a combination of logically quadrilateral and triangular finite elements
for the poloidal plane and pseudospectral collocation for the periodic
direction [Orszag71]. The  polynomials
used for finite element basis functions are selected by the user for optimal
efficiency, and poloidal mesh lines need not be orthogonal. For many fusion problems, accuracy is improved
by aligning grid lines with the equilibrium flux surfaces inside the separatrix. The grid can also be packed around low order
rational flux surfaces to efficiently resolve the small spatial scales that
arise at high S. Triangular meshing outside
the last closed flux surface allows complicated, realistic boundary shapes.
(Fig 3)
polynomials
used for finite element basis functions are selected by the user for optimal
efficiency, and poloidal mesh lines need not be orthogonal. For many fusion problems, accuracy is improved
by aligning grid lines with the equilibrium flux surfaces inside the separatrix. The grid can also be packed around low order
rational flux surfaces to efficiently resolve the small spatial scales that
arise at high S. Triangular meshing outside
the last closed flux surface allows complicated, realistic boundary shapes.
(Fig 3)
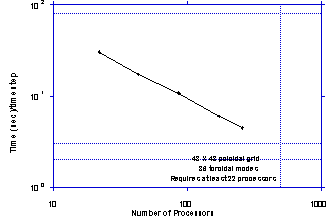 From
inception, NIMROD has been developed for implementation on distributed memory
architectures. Grid blocks allow decomposition
of the poloidal plane, and Fourier components are allocated to different layers
of processors, providing three-dimensional decomposition where each layer may
have a number of processors addressing different grid blocks. The Message Passing Interface library (MPI)
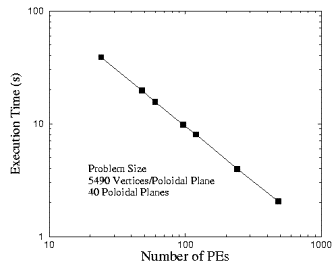
is used for communication that is portable across many platforms. With this approach, NIMROD has demonstrated
near ideal parallel scaling in production computations. An example is shown in Figure 4. Speed-up from the two types of decomposition
performed in tandem is essentially the product of the speed-up due to each
acting separately.
From
inception, NIMROD has been developed for implementation on distributed memory
architectures. Grid blocks allow decomposition
of the poloidal plane, and Fourier components are allocated to different layers
of processors, providing three-dimensional decomposition where each layer may
have a number of processors addressing different grid blocks. The Message Passing Interface library (MPI)
is used for communication that is portable across many platforms. With this approach, NIMROD has demonstrated
near ideal parallel scaling in production computations. An example is shown in Figure 4. Speed-up from the two types of decomposition
performed in tandem is essentially the product of the speed-up due to each
acting separately.
 The NIMROD code has been extensively benchmarked
against calculations from several existing fusion codes, such as DEBS, GATO,
FAR, MARS and M3D. Validation problems
include linear ideal and resistive MHD instabilities in slab, cylindrical, and
toroidal geometry, resistive ballooning modes, nonlinear resistive tearing
modes, nonlinear kink-ballooning modes, and linear and nonlinear waves and instabilities
using two-fluid extensions. NIMROD is
presently being applied to study the dynamics of spheromaks [Sovinec01], RFPs
[Sovinec98], and tokamak experiments such as DIII-D at General Atomics in San
Diego.
The NIMROD code has been extensively benchmarked
against calculations from several existing fusion codes, such as DEBS, GATO,
FAR, MARS and M3D. Validation problems
include linear ideal and resistive MHD instabilities in slab, cylindrical, and
toroidal geometry, resistive ballooning modes, nonlinear resistive tearing
modes, nonlinear kink-ballooning modes, and linear and nonlinear waves and instabilities
using two-fluid extensions. NIMROD is
presently being applied to study the dynamics of spheromaks [Sovinec01], RFPs
[Sovinec98], and tokamak experiments such as DIII-D at General Atomics in San
Diego.
2.3.2 The M3D Code

 Multilevel
3D (or M3D)[Park99] is a parallel code that is especially suited for geometries
with inherently three-dimensional boundaries, e.g. stellarators, but can also
be used to simulate axisymmetric devices. M3D consists of two parts, a mesh module and a physics module.
The mesh module contains the grid, implementation of differential and integral
operators, I/O, and inter-processor communication. The physics module handles time advancement of the equations and
contains a hierarchy of physics levels that can be invoked to resolve increasingly
complete phase-spaces, and therefore provide increasing realism. The module includes
resistive MHD, two-fluid, and kinetic particles. Electrons are represented as a fluid with an approximate fluid
closure. M3D uses a stream function/potential
representation for the magnetic vector potential and velocity that has been designed
to minimize spectral pollution. Parallel
thermal conduction is simulated with the "artificial sound" method
[Park86]. The solution algorithm is quasi-implicit in that only the most
time-step limiting terms including the compressional Alfvén wave and field diffusion
terms are implemented implicitly, with explicit time stepping used for the remaining
terms.
Multilevel
3D (or M3D)[Park99] is a parallel code that is especially suited for geometries
with inherently three-dimensional boundaries, e.g. stellarators, but can also
be used to simulate axisymmetric devices. M3D consists of two parts, a mesh module and a physics module.
The mesh module contains the grid, implementation of differential and integral
operators, I/O, and inter-processor communication. The physics module handles time advancement of the equations and
contains a hierarchy of physics levels that can be invoked to resolve increasingly
complete phase-spaces, and therefore provide increasing realism. The module includes
resistive MHD, two-fluid, and kinetic particles. Electrons are represented as a fluid with an approximate fluid
closure. M3D uses a stream function/potential
representation for the magnetic vector potential and velocity that has been designed
to minimize spectral pollution. Parallel
thermal conduction is simulated with the "artificial sound" method
[Park86]. The solution algorithm is quasi-implicit in that only the most
time-step limiting terms including the compressional Alfvén wave and field diffusion
terms are implemented implicitly, with explicit time stepping used for the remaining
terms.
 M3D
has several mesh modules: the original structured module uses radial finite
differences and is spectral in poloidal and toroidal angles. Another mesh module, suitable for tokamaks,
has triangular and quadrilateral finite elements in the poloidal plane and is
spectral in the toroidal angle.
Finally, there is the three-dimensional mesh module, which has been
fully implemented with 3D MPI based domain decomposition for MPP platforms. This is the version to be further developed
in this proposal.
M3D
has several mesh modules: the original structured module uses radial finite
differences and is spectral in poloidal and toroidal angles. Another mesh module, suitable for tokamaks,
has triangular and quadrilateral finite elements in the poloidal plane and is
spectral in the toroidal angle.
Finally, there is the three-dimensional mesh module, which has been
fully implemented with 3D MPI based domain decomposition for MPP platforms. This is the version to be further developed
in this proposal.
 A three-dimensional mesh is utilized to
facilitate the resolution of multi-scale spatial structures, such as reconnection
layers and to accommodate fully three-dimensional boundary conditions that
occur in stellarators or the evolving free boundary of a tokamak bounded by a
separatrix. The mesh uses unstructured,
3D piecewise-linear triangular finite elements in the poloidal sections. The domain decomposition consists of slicing
the toroidal geometry into a set of poloidal planes with each poloidal plane
further partitioned into equal area patches.
One or more of the poloidal patches are assigned to each processor. The fluid part of each time step consists of
uncoupled 2D scalar elliptic equations that are solved concurrently within each
poloidal plane. The PETSc library has
been used extensively to provide a portable, efficient parallel implementation
for the elliptic equations that need solution at each time step. These are
solved with a Krylov accelerated iterative scheme that uses the overlapped
Schwarz method for preconditioning.
This leads to excellent parallel scalability.
A three-dimensional mesh is utilized to
facilitate the resolution of multi-scale spatial structures, such as reconnection
layers and to accommodate fully three-dimensional boundary conditions that
occur in stellarators or the evolving free boundary of a tokamak bounded by a
separatrix. The mesh uses unstructured,
3D piecewise-linear triangular finite elements in the poloidal sections. The domain decomposition consists of slicing
the toroidal geometry into a set of poloidal planes with each poloidal plane
further partitioned into equal area patches.
One or more of the poloidal patches are assigned to each processor. The fluid part of each time step consists of
uncoupled 2D scalar elliptic equations that are solved concurrently within each
poloidal plane. The PETSc library has
been used extensively to provide a portable, efficient parallel implementation
for the elliptic equations that need solution at each time step. These are
solved with a Krylov accelerated iterative scheme that uses the overlapped
Schwarz method for preconditioning.
This leads to excellent parallel scalability.
The M3D Team has a broad experience base in using the extended MHD formulation in fusion simulations [Sugiyama00]. The M3D Team also has significant experience with kinetic formulations including fluid bulk species plus a simulation-particle energetic ion population, a hybrid formulation with fluid electrons and simulation-particle ions [Fu95]. Historically, the M3D formulation was the first to identify a new nonlinear disruption mechanism in the TFTR high-power DT fusion experiments [Park95]. M3D has also been used to study disruption prevention techniques such as massive impurity injection [Strauss98].
2.3.3 Required
Computational Resources
We can estimate the computational resources required to
carry out the necessary simulations for parameters typical of present and
proposed experiments as shown in Table I. TABLE I: Typical dimensionless
parameters for present and proposed
experiments
|
parameter |
name |
CDXU |
NSTX |
CMOD |
DIII-D |
FIRE |
ITER |
|
R (m) |
Major radius |
0.3 |
0.8 |
0.6 |
1.6 |
2.0 |
5.0 |
|
Te [keV] |
Elec. Temp. |
0.1 |
1.0 |
2.0 |
2.0 |
10 |
10 |
|
b |
Plasma beta |
0.01 |
0.15 |
0.02 |
0.04 |
0.02 |
0.02 |
|
S1/2 |
Inv resis. length |
200 |
2600 |
3000 |
6000 |
20,000 |
60,000 |
|
(r*) –1 =Ba/T1/2 |
Ion number |
40 |
60 |
400 |
250 |
500 |
1,200 |
|
a/le |
Recip. norm elec skin depth |
250 |
500 |
1000 |
1000 |
1500 |
3000 |
Estimates based on explicit time-stepping with no grid refinement: Let us first estimate the computational requirements for a 3D calculation with uniform zoning of size Dx and a explicit time-stepping scheme based on the CFL criteria for the poloidal Alfven wave, i.e. Dt = Dx / VAP. For a 3D mesh of linear dimension N, i.e., N3 mesh total mesh points, it would take N time steps to calculate one Alfven wave transit time tA = a / VAP. Typical ideal and resistive MHD instabilities would grow on the timescales TIDEAL ~ b-1/2 tA and TRESIS ~ S1/2 tA , requiring about b-1/2 N and S1/2 N time-steps, respectively. Thus, the total number of space-time points required to compute an ideal or resistive instability would be about b-1/2 N4 (ideal) and S1/2 N4 (resistive)
Current experience shows that with real performance of about 100 MFLOPS/processor and of order 1000 processor-hours, we can compute a problem with 1003 mesh points for 10**4 time steps, using a complex fluid model with the compressional wave and field terms implemented implicitly. This is about 1010 space-time points in 3 ´ 1014 operations. This is easily sufficient resolution and timesteps to calculate an ideal mode in CDX-U, and is nearly sufficient to study the initial growth phase of a nonlinear tearing mode. We see this since the number of linear mesh points is comparable to: the linear tearing-layer width, S½, the ratio of the system size to the ion Larmor radius r*, and the ratio of the system size to the electron collisionless skin depth, a/le. These are the relevant lengths that enter the two-fluid XMHD model.
The question is: what type of computer power is needed to study this physics in a larger, hotter device with a stronger magnetic field? We see from Table I. that depending on what scale length needs to be resolved, the number of mesh points in a linear direction will increase by about an order of magnitude as we go from CDX-U to DIII-D. The increase in the total number of space-time points would be the fourth power of this factor times another scaling factor that will between unity (for ideal scaling) to about 10 (for resistive scaling). Thus, the number of space-time points required would increase anywhere from 104 to 105. Running on a 10 Teraflop (delivered) computer for 3 days would correspond to about 3 ´ 1018 floating point operations which would be about 104 times greater than what was quoted above for what is available to us today, so a full DIII-D calculation might be feasible with this hardware increase alone.
Grid refinement, implicit time stepping and improved algorithms: It is straightforward to see that the above scaling estimates can be gross overestimates if we take into account improved algorithms and meshing. For example, for a field-line following mesh and with adaptive mesh refinement, the total number of mesh points should only have to grow linearly as we go to larger machines and higher resolution, rather than cubic. With implicit time differencing, the time step will not have to decrease nearly as fast as linear with zone size. More efficient solvers can give an additional factor. Thus, with these computational improvements, some of which have already been implement to varying degree in M3D and NIMROD, we can realistically expect to be able to calculate modes using XMHD models in DIII-D, NSTX, and CMOD in the time frame of this proposal, and even FIRE and ITER calculations might be within reach. Of course, it also may not be necessary to simulate the exact parameters of a machine if we can determine scaling relations from doing a series of calculations at reduced parameters.
Hybrid particle/fluid models will take additional resources, methods such as df are very efficient in that they only represent the difference from a Maxwellian as particles. One of our primary goals is to develop accurate and efficient models with which we can do meaningful calculations on the computer power available to us.
3. Research Design and Methods
Since many physical effects with radically different time and spatial scales contribute to the overall behavior of modern fusion experiments, predictive macroscopic simulation capability requires a sophisticated numerical approach based on an optimal physics-model formulation that is developed with a vision toward harnessing tremendous computing resources. The proposed center will create a unique opportunity to meet the challenges of macroscopic fusion simulation by synthesizing the individual elements introduced in Section 1.4. The goal for each element is summarized as follows:
· Code Development—the spatial and temporal stiffness of models describing macroscopic plasma behavior defies straightforward numerical implementation, irrespective of any conceivable level of computing power. The code development component of CEMM will employ the best numerical methods for solving the extended-MHD fluid models recommended by our theoretical component.
· Model Development—fluid models and closure relations derived from the fundamental kinetic description for plasmas acquire different forms under different approximations and manipulation. The theoretical component of CEMM will analytically refine the fluid model, and the heat-flux and stress-tensor closure terms describing kinetic effects, for optimal accuracy and numerical tractability, and will define test problems with analytic solutions for code validation.
· Visualization and Data Management—successful simulation of macroscopic plasma behavior requires successful diagnosis of results before a better physical understanding can be achieved. The visualization and data management component of CEMM will seek to extract the maximum amount of information possible and to provide a convenient means for data access, storage, and comparison with experimental results.
· Computer Science Enabling Technologies (CSET)—with the multitude of challenges confronted in macroscopic plasma simulation, code efficiency is a paramount issue. The CSET component of CEMM relies on several computer science projects that focus on parallel algorithm optimization and managing code complexity. We include in this category code support and dissemination.
· Applications and Validation—This is an aggressive program to pioneer new applications enabled by the new capabilities, to compare the results of the two codes NIMROD and M3D with one another and with experimental data.
Each component is an essential ingredient of the unique, unified technical effort of the proposed CEMM. Development and deployment of the two complementary simulation codes are viewed as the critical-path elements for the first years of CEMM. This is reflected in the proposed budget allocations for the NIMROD and M3D groups. CEMM will primarily rely on existing programmatic fusion funding for its theoretical support and on associated OSCAR funding for the CSET activities.
The remainder of Section 3 describes the technical approach that will be applied by each of the individual CEMM components and the management plan for coordination.
3.1 Code
Development
We are proposing a major expansion of physics simulation capabilities for both the NIMROD and M3D codes through three strategic areas of code development: 1) expanded use of implicit techniques, 2) kinetic closures for majority species, and 3) improved and adaptive meshing capabilities. The first will facilitate practical computation with the two-fluid model and with strong advection. The second will implement the kinetic based closures described in Sections 3.2.2 and 3.2.3. The third area will facilitate efficient computation of the extreme difference in spatial scale lengths arising in extended-MHD physics. These developments will draw from advances in the CSET products as indicated below. Furthermore, modular coding will be pursued to make the same advances accessible to both codes.
3.1.1 Expanded Use of Implicit Techniques
The stiff system of equations describing extended-MHD cannot be addressed in a purely explicit manner. Our approach to this computational challenge is the use of implicit and semi-implicit methods in the advance of the solution field. For single-fluid dynamics, the linearized ideal MHD system of equations is self-adjoint, leading to a Hermitian numerical operator. However, effects beyond the scope of the basic single-fluid model make the system non-self-adjoint. Therefore, modeling these effects in large-scale simulations without prohibitive restrictions on time step will require the solution of non-Hermitian matrices. The objectives for this development area are:
·
Revise the
magnetic field advance to improve treatment of the Hall term.
A symmetric numerical operator is presently used in NIMROD to make the Hall advance numerically stable at large time step. Though this form is consistent with the partial differential equations, at the time steps needed for modeling macroscopic fusion phenomena, it leads to substantial inaccuracies [Harned89], including artificially large magnetic reconnection rates. With capabilities for solving non-Hermitian matrices, a more accurate semi-implicit scheme is available [Harned89]. It uses a fourth-order in space, second-order in time numerical operator derived using the method of differential approximation discussed in [Caramana91]. The finite element representations in M3D and NIMROD are suitable for derivatives of order 2 or less, so this scheme requires an auxiliary vector that represents second derivatives of the new magnetic field, while the advance uses second derivatives of the auxiliary vector. Since this operator is based on a linearized Hall term, electron viscosity will be needed for nonlinear applications to truncate power flow at the smallest resolved scales.
·
Incorporate
gyroviscosity free of time-step restriction.
The magnetic moment of charged particles gyrating about a
magnetic field leads to collision-independent terms in the stress tensor. Their coefficients have the same ![]() dependence as the
diamagnetic drifts induced by the Hall term in the presence of an electron
pressure gradient and should therefore be included when the two-fluid model is
used. The nonsymmetrical form of these
terms implies use of a non-Hermitian operator for numerical stability at large
time step.
dependence as the
diamagnetic drifts induced by the Hall term in the presence of an electron
pressure gradient and should therefore be included when the two-fluid model is
used. The nonsymmetrical form of these
terms implies use of a non-Hermitian operator for numerical stability at large
time step.
·
Incorporate
implicit advection.
The advective terms (![]() ) in the set of fluid equations are presently treated with an
explicit predictor/corrector algorithm [Lionello99] in the NIMROD code, where numerical
stability restricts the time step to the Courant-Friedricks-Lewy condition,
) in the set of fluid equations are presently treated with an
explicit predictor/corrector algorithm [Lionello99] in the NIMROD code, where numerical
stability restricts the time step to the Courant-Friedricks-Lewy condition, ![]() . Though NIMROD has
been successfully applied to nonlinear conditions where flows have reached several
tenths of the Alfvén speed, numerical stability greatly restricts the time
step. This can be prohibitive at high
S-values, where fine mesh spacing is required near resonant surfaces. An implicit algorithm for flow can remove
the numerical stability restriction, and this will also lead to non-Hermitian
matrices in the numerical equations.
. Though NIMROD has
been successfully applied to nonlinear conditions where flows have reached several
tenths of the Alfvén speed, numerical stability greatly restricts the time
step. This can be prohibitive at high
S-values, where fine mesh spacing is required near resonant surfaces. An implicit algorithm for flow can remove
the numerical stability restriction, and this will also lead to non-Hermitian
matrices in the numerical equations.
·
Optimize parallel algorithms for solving
non-Hermitian matrices.
We expect that iterative methods based on the Krylov subspace will provide the most efficient means for solving the non-Hermitian matrices envisioned for XMHD modeling. We have previously coupled NIMROD to the AZTEC parallel solver library [http://www.cs.sandia.gov/CRF/aztec1.html], and M3D uses the PETSc parallel solver library [http://www-fp.mcs.anl.gov/petsc/index.html]. Both of these libraries offer GMRES and transpose-free QMR. Experience with NIMROD has shown that preconditioners developed specifically for our application outperform those available in the AZTEC library [Plimpton99]. We therefore plan to use a new AZTEC capability of calling user-supplied preconditioning routines during the iterations. In addition, the anticipated collaboration with the TOPS topical center will help us optimize use of PETSc.
3.1.2 Kinetic
Closures for Majority Species
The two proposed methods for incorporating kinetic effects into the fluid equations are similar in their use of trajectory tracking to accumulate nonlocal contributions to the closure terms. They will therefore use the same parallel particle-tracking algorithm, though information gathered from it will differ in the two approaches. The tracking of trajectories is a numerical prerequisite for either closure scheme.
The objectives for this development area are:
·
Implement a
modular and efficient search algorithm.
Although trajectory tracking is common in simulations using uniform grids, it presents algorithmic challenges in highly non-uniform and/or unstructured finite element meshes. An approach already used in M3D for energetic ions tracks particle trajectories on a structured mesh only, and fields are interpolated from the nonuniform mesh to the uniform particle grid. NIMROD is presently pursuing a different approach, where particles are tracked in the nonuniform finite element mesh. Here, an efficient search algorithm is the most important requirement. We have begun implementing an approach where the vertices of each finite element are mapped from real-space coordinates to logical-space coordinates [Alejandro97], creating a look-up table for locating positions. We intended to compare efficiency and accuracy of these different approaches and then pursue the most promising of the two.
·
Implement kinetic
closures based on simulation-particles.
In this approach, df is computed along sample trajectories in phase space that coincide with the evolution of a random initial distribution of simulation particles. Particle trajectories are influenced by the time-evolving magnetic and electric fields, and the equation for each df sample uses the local fluid moment information along its trajectory. This information is gathered in statistical forms of the closure relations that are used in the advance of the fluid moments. Calculating df along each trajectory and the statistical closure relations are straightforward in the explicit time-advance envisioned for the ion species. Computational practicality then depends on the parallel efficiency of particle tracking and on the gather/scatter operations relating field and particle information.
·
Implement kinetic
closures based on the CEL approach.
The expression for heat flux that is based on the analytic CEL expansion for df [Held01] will be incorporated for simultaneous evolution with the fluid moments. The same trajectory-tracking algorithm used for simulation-particle closures will be used for the required parallel integrations. Numerical research will focus on the stiffness associated with the rapid parallel communication. We will explore a semi-implicit approach, where an explicit CEL computation of the kinetic heat flux is numerically stabilized by a 3D thermal conduction operator with local anisotropic diffusivity. Similar developments will be explored for the parallel parts of the electron stress tensor.
3.1.3 Mesh methods
With different length-scales being important in different regions of the macroscopic computational domain, efficiency is strongly dependent on effective grid layout. We will pursue improvements in mesh generation, 3D field-line following meshes, and mesh adaptivity to achieve optimal spatial resolution performance.
The objectives for this development area are:
·
Improve mesh
generation with both closed and open magnetic surfaces.
To treat Edge-Localized Modes (ELMs), it is necessary to include the magnetic field separatrix between the closed magnetic surfaces of the core, and the open surfaces of the vacuum region. Progress has been made in this area [Strauss96], but a more general method of mesh generation is needed that produces a mesh aligned with magnetic surfaces near an X point of the poloidal magnetic field.
·
Implement a
field-aligned mesh.
M3D is able to use different grid geometries on each poloidal plane. This gives the possibility of a field-line following mesh, which has been used successfully in gyrokinetic simulations [Lin00]. Each meshpoint is displaced from its position on the previous poloidal plane by integrating along a field line of the equilibrium magnetic field. The displacement can be slightly altered to ensure that after a full toroidal rotation, each meshpoint coincides with a meshpoint of the initial poloidal plane. If the magnetic field has significant shear, the cells of the mesh will become highly distorted. This can be avoided by reconnecting triangular mesh cells, to get a good quality mesh. An advantage of a field line following mesh is that, since unstable modes tend to have little structure along field lines, the mesh can be very efficient for representing the modes. This is particularly important for short wavelength modes, such as occur in ballooning mode turbulence, or in a turbulent 3D reconnection layer. Another possible advantage is in parallel thermal transport along the magnetic field, by decreasing cross-field aliasing.
·
Investigate mesh
adaptivity.
As we move to a more sophisticated and computationally intensive modeling, we will have to deal with extremely fine scale dynamical processes. For simple resistive reconnection, the reconnection layer can be resolved by a simple refinement in a radial flux coordinate. When more physics is included, it may be necessary to resolve fine scale structure occurring in the reconnection layer. To deal with this, one needs to refine the mesh in the poloidal angle, and perhaps also in toroidal angle. This can be done readily with a mesh of triangular and rectangular elements. As a first step, the refinement can be done statically because the magnetic field does not change a great deal, even during reconnection. Later, we will refine the mesh dynamically. The main difficulty is to distribute the mesh across processors to maintain load balance. In this area, we expect to benefit from the research program of the Terascale Simulation Tools Technology Center.
3.2 Model Development
Comprehensive
macroscopic plasma simulation requires assembling analytic and numerical
techniques to extend large-scale fluid computation to include two-fluid and kinetic
effects. In contrast to resistive MHD,
two-fluid modeling is not well established, even without kinetic effects. This model is required for typical tokamak
parameters, where thermal speeds exceed bulk fluid motions. Here, thermally induced particle drifts lead
to significant differences between electron and ion fluid motions perpendicular
to the magnetic field. Many different
formulations describing this ordering of terms have been derived [Hazeltine92],
but until recently, few have been successfully implemented for large-scale
nonlinear simulation [Sugiyama00]. The
goal of theoretical model development for this level is to refine the
formulation for computational tractability.
Particular attention will be paid to terms like
"gyroviscosity" arising in the stress tensor due to spatial
variations of particle magnetic moments.
In this case, analytic cancellation with advective terms (of the form ![]() ) can lead to variants of the two-fluid model that are easier
to solve numerically [Sugiyama00].
) can lead to variants of the two-fluid model that are easier
to solve numerically [Sugiyama00].
Important kinetic
effects that require numerical modeling also arise in macroscopic behavior. In some cases, the important behavior
involves a minority population of energetic ions, where large gyro-orbit
effects change the nature of macroscopic MHD modes. Simulation particles have already been used in M3D to model such
cases [Fu95]. Models and approaches
used for the energetic ion component lay a foundation for a more comprehensive
level, where the majority species fluid equations are closed with numerical
computations of heat flux and stress.
This is required for simulating the nonlocal effects associated with the
free streaming of majority-species particles parallel to magnetic field lines,
such as the neoclassical effects described earlier, and for large gyro-orbit effects
of the majority ion population.
Numerical methods for this comprehensive level of nonlinear macroscopic
simulation are in their infancy. It
will therefore receive the largest share of the model development efforts of
CEMM, using the approaches outlined in Sections 3.2.1-3.2.3.
3.2.1 Kinetic Modeling Framework
Parallel particle streaming and large ion gyro-orbits lead to important kinetic effects in fusion plasmas; these effects may often be described by small deviations from a Maxwellian distribution that is parameterized by density and temperature profiles. This concept has led to improved numerical performance of particle-based simulation of microscopic plasma behavior [Parker93], and it is used in the M3D simulations for energetic ions [Fu95]. It also serves as the framework for a more general kinetic macroscopic simulation, but the Maxwellian distributions must evolve in time to keep kinetic deviations small. The fluid equations with closure information from the kinetic distortions will be used to advance the Maxwellian distributions, while the kinetic distortions (df) are advanced using the fluid moment variations encountered along particle trajectories. There are two realizations of this approach: one integrates the df distribution function along a sample set of characteristics, and the other uses an analytic Chapman-Enskog-Like (CEL) expansion of the kinetic distortion in velocity-space. [Chang92] These approaches are complementary in that the former is more appropriate for describing ion kinetics, while the latter is better suited for electron kinetics. Together, they will provide comprehensive kinetic modeling that can be included in macroscopic plasma simulations.
3.2.2 Kinetic Modeling through Simulation Particles
In this approach, trajectories in phase space are evolved numerically, subject to the electric and magnetic forces encountered by a physical particle, except for gyro-orbit motions that are included through the numerical averaging of gyrokinetics [Lee88]. The trajectories serve as characteristics where the kinetic distortion, df, is computed from the fluid moments that are encountered. The heat flux and stress tensor at a physical location are then computed statistically from the characteristics in the vicinity of that physical location at a given point in time. Heat flux for species a, for example, appears as
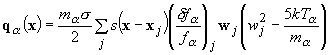 (1)
(1)
where ![]() is a shape function
for simulation particle j, wj is the difference between the particle's velocity and
the local fluid velocity for species a,
and s is a normalization factor. Equation (1) has the same form as the
analytic definition of heat flux, except (1) contains a correction term to eliminate
heat flux associated with numerical error.
This computation is then used in the advance of the fluid pressure for
species a, and a similar term for
kinetic stress appears in the fluid velocity equation. Other than these closure terms, the fluid
advance is the same as what is used for the two-fluid model without kinetic
effects; the fluid part of the algorithm is fundamentally unchanged. This was the intent of early formulations of
this evolving-Maxwellian/df approach.
[Nebel94].
is a shape function
for simulation particle j, wj is the difference between the particle's velocity and
the local fluid velocity for species a,
and s is a normalization factor. Equation (1) has the same form as the
analytic definition of heat flux, except (1) contains a correction term to eliminate
heat flux associated with numerical error.
This computation is then used in the advance of the fluid pressure for
species a, and a similar term for
kinetic stress appears in the fluid velocity equation. Other than these closure terms, the fluid
advance is the same as what is used for the two-fluid model without kinetic
effects; the fluid part of the algorithm is fundamentally unchanged. This was the intent of early formulations of
this evolving-Maxwellian/df approach.
[Nebel94].
Model development will focus on outstanding issues that need attention before practical simulation is possible. These are 1) the filamentation of the df distribution over transport time scales, 2) the accumulation of low order moments in the df distribution due to statistical errors, and 3) the stiffness arising from unrestrained parallel motions. The first two issues improve with increasing phase space sampling, i.e. very large numbers of computed trajectories (107 is now common in microscopic modeling, and Terascale computing can bring this to 109). However, resolving the filamentation issue will need some form of collision modeling [Brunner99]. In addition, numerical corrections to eliminate low-order moment accumulation have been tested by CEMM Co-PI Sovinec and will be further investigated as model development. The stiffness issue may ultimately require implicit techniques, especially for electrons. However, ion kinetic effects arise in important macroscopic behavior where parameters are tractable with explicit computation. For this reason, the simulation-particle approach will first be applied for studying ion kinetic effects. The complementary CEL expansion described next will first be applied for studying electron kinetic effects.
3.2.3 Kinetic Modeling through Chapman-Enskog-Like Closure
The proposed CEL approach to modeling kinetic physics differs from simulation-particle closure in that the kinetic distortions are determined from analytic solutions of gyro-averaged drift-kinetic equations. These solutions are obtained via polynomial and/or rational function expansions in velocity space. In contrast to classical, collisional Chapman-Enskog closure theory, which is inappropriate for high-temperature plasmas [Chapman39], the proposed CEL expansion is based on the small parallel gradients of the evolving Maxwellian distribution. The advantage of this method is that the closure terms at a given position are expressed in terms of a single numerical integration covering parallel motion, rather than many sample phase space contributions summed statistically. The disadvantage is that analytically accounting for perpendicular gradients is more difficult. These tradeoffs make the CEL approach well suited for computation of electron kinetic effects, where fast parallel motions are paramount. Electron heat flux computations based on the proposed CEL expansion have been formulated and implemented for macroscopic simulation [Held01]. The required parallel integrations use the same trajectory-tracking algorithm that is employed for simulation-particle tracking.
Model improvements here will concentrate on developing the
CEL electron stress tensor closure to model perturbed neoclassical effects,
including the mechanisms underlying the neoclassical tearing mode described in
Section 2. Additional developments seek
to incorporate electron and ion drift phenomena. Nevertheless, it is anticipated that simulating ion gyro-orbit
effects with simulation-particle closures and nonlocal, parallel electron
dynamics with CEL closures will provide the most effective use of large-scale
computation.
3.3 Visualization and Data Management
Improvements in plasma diagnostic techniques have made it increasingly feasible to demonstrate excellent correlations between experimental results and theoretical models. In order to maximize the effectiveness of simulation/experiment comparisons, it will be necessary to address critical computer science and enabling technology issues in the area of data management and visualization. The power of advanced computing to solve critical plasma science problems can be fully exploited only if a capable infrastructure is established and effective software tools are made available. Such tools should include standardized data structures and access methods, synthetic diagnostics allowing comparisons to experimental diagnostics, standard analysis and visualization utilities, and common code interfaces. In a broader sense for the entire national fusion community, these issues will be addressed in the National Fusion Collaboratory discussed in Section 3.4. Specific to this proposal, we will address near term data management and visualization issues directly related to NIMROD and M3D.
We will build on and greatly expand a pilot project begun under PSACI funding, to create the infrastructure to store results of NIMROD and M3D into the MDSplus data management system. MDSplus is a client/server system that has been used in the experimental community (C-Mod, DIII-D, NSTX) to provide a common, shared, secured, network interface to all data. Storage of our simulation results in MDSplus will greatly facilitate their comparison to experimental data and will aid in the validation of code results as well as the analysis of experimental data.
Accompanying the deployment of an MDSplus based data storage system will be the development of a database management system, which keeps track of this data, supports searches of the database, and provides a convenient interface to the data manipulation and visualization system described below. The Microsoft SQL Server is being used in the experimental community to catalogue large experimental code runs. This system will be extended to allow tracking of runs by the two MHD codes that will be coupled to MDSplus. Management tools will be developed that will work with the anticipated high dimensional data objects which will be critical to the success of our research. Such management will include a high degree of feedback and iteration between data and experimental model. Comparison of datasets will be critical so that simulations can be validated against experimental data.
Presently the plasma sciences are doing interactive visualization of three-dimensional objects such as the temporal evolution of the plasma temperature profile. As our research moves towards higher dimensional data objects an exploration tool will be created to allow easy visualization of this complex data. This tool will be used to find correlations, to visualize subspaces, to find data that is characterized by a particular program or formula, and mapping between relational, object oriented, and other databases. Such tools will need to provide operations or methods over the data such as spatial proximity, "like images," or subsets of arrays. These capabilities will be fundamental to comparing experimental data with simulation results thereby allowing validation of any theoretical model. Finally, such complex visualization must analyze efficiency issues related to searching, optimized performance over networks, and organization of data based on access efficiency needs.
3.4 Computer Science Enabling Technologies
We will interface with existing and proposed computer science and numerical analysis efforts to make improvements in linear algebra, visualization, code management, and data management capabilities of the NIMROD and M3D codes.
We have agreed to collaboration with the Terascale Simulation Tools and Technologies (TSTT) Center with Dr. James Glimm as Principal Investigator. The TSTT Center will focus on the incorporation of “standard” grid generation and discretization libraries into the M3D code, and possibly the NIMROD code. This will greatly simplify code structure and subsequent code development and will enable the seamless incorporation of higher-order and other advanced capabilities in these areas. We will also explore with them the feasibility of combining potential and field advance equations to increase both the accuracy and efficiency of both.
We will also use developments from the Terascale Optimal PDE Simulations (TOPS) Center with Dr. David Keyes as the Principal Investigator. The TOPS Center proposal will focus on extending the sparse matrix solvers in PETSc in several ways that will improve the efficiency of M3D. One of their primary goals is the development of multilevel solvers that handle the full multicomponent coupling of stiff systems of PDEs. Included in this is the addition of nonlinear Schwarz domain decomposition, algebraic multigrid methods, and refinements in the implementation of several PETSc routines to improve their cache utilization and hence performance.
We are also participating in a CSET proposal on adaptive algorithms and high performance software submitted with Dr. Phil Collela as Principal Investigator, called “An Algorithmic and Software Framework for Applied Partial Differential Equations”. We will work with them to develop an adaptive mesh refinement (AMR) capability and to perform and evaluate comparison tests with M3D and with NIMROD.
We will work with the National Fusion Collaboratory Pilot project proposed to the Office of Science under SciDAC Notice 01-06. Several of the goals of this Collaboratory are well aligned with our own goals. These include: allowing for more efficient integration of experiment, theory, and modeling; easier access to simulation codes; and increased productivity of code developers through enhancements in communication capabilities for shared code development projects. To assure that we have continual contact with the Collaboratory project and to assure that their work will benefit our effort, one of our Co-PIs, Dr. Sovinec, will be a member of their Project Oversight Committee.
Please refer to the three collaboration letters in Appendix B from the TSTT, TOPS, and the adaptive algorithms Centers. We have had extensive discussions with these three teams in which workscope and personnel exchanges have been discussed and agreed to. We consider these elements to be important and essential components of our proposal. As previously discussed, there will be no OFES funding requested for these activities.
3.4.1 Code Support and Dissemination
The software being developed under this proposal will be made fully available to others in the fusion program. The participating teams in this project are committed to code support and dissemination.
Since its inception in 1996, a goal of the NIMROD project has been to provide a simulation tool for the fusion community that is documented, publicly available, and relatively user friendly. NIMROD is an open source project. The source code, and all of its supporting software, is available for free download at the NIMROD web site: http://www.nimrodteam.org. Documentation, a validation code library, and other information is also available from the web site. The NIMROD team provides personal consultation and support for users as requested. We are currently supporting users from General Atomics, LLNL, UCLA, and the University of Washington.
The M3D code likewise has a strong commitment in this area. This is facilitated by the PPPL Computational Plasma Physics Group (CPPG) who assist with the installation of the code on new hardware platforms and provide the first-tier consultation and support services. A home page for the M3D project can be found in the area: https://w3.pppl.gov/topdac (and associated links)
3.5 Applications
Applications are an essential part of the proposed CEMM. While we expect these efforts to be funded primarily out of the mainline OFES theory program, they are described here to provide the context for the code and model development effort. We also recognize that computational models will not gain general acceptance unless they are proven to give useful results, and real applications tend to drive the development of the models.
We have a special commitment to perform the applications called out in the next five subsections and to interact with the space physics community to promote the applicability of the software developed here on those problems. In addition, we have collaboration letters with the Science Leaders of the U.S. fusion Experiments, NSTX, and CMOD, (See Appendix B) for the CEMM to serve as a resource to aid in the interpretation of new and unique phenomena detected in those experiments. Thus, for example, we expect to apply these codes to the study of Internal Reconnection Events (IREs) in NSTX and to transport-barrier induced MHD modes in CMOD.
3.5.1
Extended MHD Simulation of Neoclassical Tearing Modes in Tokamaks
We
are proposing to simulate neoclassical tearing mode observed in D3D (see
Section 2.1) and to thereby assess the suitability of our codes for analyzing
other experimental situations where NTM's are observed and for the design of
future machines. We are first proposing
to study the seed island generation for the NTM driven by the internal kink
mode and also field errors as a function of resistivity and rotation. We will next test the predicted island
saturation levels from the neoclassical closures with that observed in the
experiment. The theoretical aspect of CEMM seeks to overcome problems with present
closures and to compare different closure approaches. The third (and most
difficult) issue is the threshold dynamics of the NTM. A threshold mechanism is caused by the
neoclassical enhancement of the polarization current. We are proposing to add a suitable closure form to reproduce this
effect, and to complete a comprehensive study of the resulting threshold
mechanism. Finally, we propose to study
the active stabilization of the NTM, which is in line with experimental work proceeding
on DIII-D and ASDEX. The work will entail implementing a model of RF-induced
currents in 3D island geometry.
3.5.2
Edge Localized Modes (ELMs)
Edge Localized Modes, or ELMs, are MHD-like modes with
moderately high toroidal mode number of about 10-15 located at the
separatrix, the boundary between open and closed magnetic field lines. A
large experimental lore exists about what type of ELM occurs under what
conditions. These have been given names such as “Type-n ELMs” (where
n=1,2,3), “Grassy ELMs”, etc. However, no all-encompassing theory exists to explain
the different types of ELMs that occur, or to predict what type of ELM will
occur in a future experiment.
Simulations that include the separatrix can predict this phenomenon with
the extended MHD equations. We plan to make a mesh suitable for
separatrix geometry encompassing open and closed magnetic surfaces. We will then perform high-resolution
nonlinear simulations of localized XMHD modes and observe the relaxation
phenomena and transport across the separatrix, and study the experimental
trends associated with ELMs.
3.5.3 Burning Plasmas
The next generation of magnetic fusion device, e.g., FIRE [Meade99] and ARIES [Jardin97], will be dominated by a significant fraction of energetic alpha particles and will be in a new parameter regime characterized by small normalized gyroradius and small collisionality. The high leverage research areas here are: Internal kink stabilization (or giant sawtooth): There is an unresolved issue of under what conditions the energetic a-particle and other XMHD stabilization of the sawtooth will cause the mode to delay while the driving energy builds up, and eventually lead to disruption when it does occur. Energetic particle modes (TAE and fishbone): What is the nonlinear saturation amplitude of the energetic particle modes that are predicted to be linearly unstable. Under what conditions will these modes cause significant energy loss? Resistive Instabilities: Many otherwise attractive operating regimes have significant bootstrap currents and are at low collisionality. This leads to the possibility of unstable neoclassical tearing modes. The stabilizing influence, if any, of energetic particles and other XMHD effects on these and on classical tearing instabilities is largely uninvestigated.
3.5.4 Electromagnetic Relaxation in Alternative Concept
Devices
The placement of magnetic field and current density are highly controlled during the standard operation of tokamaks and stellarators to avoid electromagnetic activity. In contrast, profile relaxation through electromagnetic activity is a characteristic of alternative concept devices such as the reversed-field pinch (RFP) and spheromak. Resistive MHD instabilities saturate through nonlinear coupling, but the accompanying magnetic fluctuations affect plasma confinement properties. The NIMROD code was used to perform the first studies of spheromak formation and sustainment through 3D electromagnetic activity [Sovinec01], and it is presently being used to study toroidal geometry effects in RFPs [Sovinec98]. With the extended MHD modeling advances proposed here, we will be able to study two-fluid effects and stochastic field transport associated with kinetic effects in these devices. In addition, electromagnetic relaxation is thought to play a major role in astrophysical accretion-disk dynamos. The geometric flexibility of both NIMROD and M3D allow users to apply them to problems outside magnetic fusion (see Section 3.5.6), and preliminary accretion-disk computations have been performed with NIMROD.
3.5.5 Stellarator Stochasticity and Stability
A critical issue for stellarators is the existence of regions of stochastic magnetic field lines that would effectively lead to poor confinement properties due to fast parallel transport. An assessment of the magnetic field structure requires the use of a 3D resistive MHD code that allows magnetic reconnection to take place. Realistic simulation of the profiles also requires parallel and cross-field thermal conduction to introduce pressure flattening in the vicinity of islands. We also plan to study stellarator stability. M3D simulations using the MHD model have given results consistent with the beta limits calculated with Terpsichore.[FU00]. Further studies will be done with resistive MHD. Neither resistive MHD nor extended MHD simulations have been made for stellarator configurations and so an understanding of the onset and consequences of the current and pressure limits is largely based on theoretical conjecture. Furthermore, the ability to study energetic particle effects on instabilities is expected to yield new and unforeseen results in this configuration. We plan to complete comprehensive studies of stellarator stability.
3.5.6 Applications
Outside Fusion
The proposed center will be a pioneer in the development of models suitable for the study of low-frequency XMHD plasma phenomena. We therefore expect the modeling approaches, numerical algorithms, and scientific simulation codes developed by CEMM to be applied to plasma and magneto-fluid problems outside fusion. Effects such as energetic ion populations, finite-size orbits (gyro-, drift-), electron transport along the magnetic field line and two-fluid terms are of more general interest for improved understanding of low-frequency macroscopic space, solar and astrophysical plasma processes. Examples where kinetic MHD models are beginning to be introduced include Alfvén waves driven unstable by energetic ring-current ions in the magnetosphere and electron acceleration due to parallel electric fields in the auroral ionosphere. The closure models discussed here may also lead to better ways of incorporating collisionless dissipation for studies of interstellar media turbulence and other reconnection processes. Furthermore, the geometric flexibility of the NIMROD and M3D codes will make them suitable for direct application to many of these problems, as indicted in Section 3.5.4 above. The XMHD models in M3D and NIMROD will also allow state-of-the-art calculations of magnetic reconnection in full 3D configurations. The model development and results in this area will be of great interest to the space and solar physics community.
3.6 Management Plan and Schedule
CEMM will add 6-7 new young scientists to the program. It will also provide close collaborations with several CSET teams (see Section 3.5) who have collaboration agreements with us. (See Appendix B for letters) Along with this new talent, we can expect that considerable “base program” funding will be used for both theoretical and computational physics support of these activities and for experimental comparisons. We plan for our Center to function exactly like that: to indeed be a center for theoretical, computational, and experimental discussions and comparison of XMHD behavior in fusion devices. However, we emphasize that all new funding will be devoted to the further development, improvement, and dissemination of the major code lines NIMROD and M3D
3.6.1 Management Plan
The Director of CEMM will be, Dr. Stephen C. Jardin (Jardin@pppl.gov), who will facilitate technical integration, oversee the logistics of schedule and budget, provide day-to-day coordination of activities and seek to achieve consensus on all issues at the strategic level. A technical lead, or PI, will be responsible for each of the technical teams within the Center: Dalton Schnack for NIMROD, Wonchull Park for M3D, Dave Schissel for the data-management and visualization area, and Professor James Callen for the theoretical liaison activities.
An experiment liaison will be named for each of the major fusion experiments, DIII-D, NSTX, and CMOD. We have reached collaborative agreements with the management of each of these facilities. Letters of support detailing some of the physics issues to be addressed appear in Appendix B.
The “staff” of CEMM will consist of the senior scientists listed on the cover page who are already established within the fusion program, and the 6-7 new staff that will be enabled by the new SCIDAC funds. The CEMM director will assign a lead technical liaison with each of our partner CSET activities that receives funding.
The Center will function by way of team meetings at a frequency to be decided later, but not more than 4-times and not less than 2-times per year. These meetings will be supplemented by both audio and video conferencing, making use of collaboration tools available now and provided through the fusion collaboratory proposal, including Showstation and Realplayer video. The Director, technical leads, and technical liaisons will perform management functions.
It is also the Director’s responsibility to ensure that the results of the CEMM are being disseminated, and that we are abreast of the latest developments in computational science. He will thus ensure adequate representation of CEMM activities at APS Division of Computational Physics meetings, SIAM and Supercomputing meetings, and other appropriate conferences. We will also make regular contact with our CSET partners
3.6.2 Schedule and Deliverables
The following activities and accomplishments are scheduled for the 3 years of the proposal:
Year 1:
·
Expand the
M3D MPP mesh module by incorporating field-line-following mesh and
carry out stellarator MHD simulations.
·
Move the
M3D two-fluid/anisotropic pressure level to MPP architecture and apply to tokamaks
and ST's.
·
Develop MPP
architecture energetic particle module for both M3D and NIMROD, and apply to
TAE and fishbone modes in tokamaks and ST's.
·
Implement
parallel non-Hermitian matrix solves in NIMROD.
· Modeling efforts will resolve what form of gyroviscosity is most appropriate and develop the CEL-based stress tensor for electrons.
Year 2:
·
Develop M3D
MPP mesh for modeling separatrix and apply to ELMs.
·
Continue
development of two-fluid-level closure schemes for axisymmetric and
non-axisymmetric systems; apply to neoclassical physics in stellarators.
·
Apply
energetic particle/MHD hybrid level to stellarators
·
Implement
majority ion df computation and closure based on
simulation particles.
·
Implement
the majority electron closures based on CEL.
· The Hall and gyroviscous advances in NIMROD will be changed to use the non-Hermitian matrix capability, improving the time advance algorithm.
Year 3:
·
Work on
adaptive mesh refinement methods and apply to global simulations that contain
near-singular structures such as reconnection layers.
·
Further
development of multi-fluid closures, including higher order moments and
parallel dynamics.
·
Incorporate
bulk ion particles in MPP: apply to tokamaks, ST, stellarators.
·
Implement
collisional effects in the simulation-particle df to address distribution function filamentation.
·
Analyze the
efficacy of semi-implicit approaches used with CEL closures, addressing the
stiffness associated with electron parallel
·
Incorporate
implicit advection for the fluid part of the algorithm.
4.
Subcontract or Consortium Arrangements:
The CEMM consists of participants from 10 different
institutions, plus those from the CSET program listed in Sec. 3.5 above. The 10 traditionally fusion institutions
participating are: Princeton Plasma Physics Laboratory, Science Applications
International Corp., Massachusetts Institute of Technology, Los
Alamos National Laboratory, New York University, University of
Colorado, General Atomics, Utah State University, University of
Texas, and the University of Wisconsin.
Each participating institution is requesting direct funding from
DOE/OFES as indicated in the budget pages, with the exception of the University
of Texas, where Waelbroeck will participate without new funds as part of the
his base-funding activities under OFES/DOE grant DE-FG03-96ER-54346. Also, the
collaborative participation of Callen and Hegna of the University of Wisconsin
is covered under their current OFES/DOE grant DE-FG02-86ER53218. Our CSET partners
are requesting separate funding from SCIDAC proposals directed to DOE/OSCAR.
Literature
Cited
[Alejandro97] Alejandro Allievi and Rodolfo Bermejo, JCP, 132, (1997)
[Aydemir92] A.Y.Aydemir, Phys. Fluids, 4 3469 (1992)
[Belova98] E. V. Belova, W. Park, G. Fu, et al, “Proceedings
of the Workshop on Nonlinear MHD and Extended MHD”, Univ of Wisconsin Center
for Plasma Theory Report UW-CPTC-98-1(1998)
[Bernard81] L.C. Bernard, F.J.
Helton, and R.W. Moore, Comput. Phys. Commun. 24, 377 (1981)
[Bondeson92] A. Bondeson, G. Vlad,
and H. Lutjens, Phys. Fluids B4,
1889 (1992)
[Bowers71] E.Bowers and N.K.
Winsor, Phys Fluids 14 2203 (1971)
[Braginskii65] [S. I. Braginskii, “Transport processes in a plasma,” Reviews of Modern Physics, 205 (Consultants Bureau, New York, 1965).].
[Brunner99] S. Brunner, E. Valeo, J. Krommes, Phys. Plasmas 6
4504 (1999)
[Callen86] J.D. Callen, W.X. Qu,
K.D. Siebert, et al, "Neoclassical MHD Equations, Instabilities and
Transport in Tokamaks," Plasma
Physics and Controlled Nuclear Fusion Research 1986 (IAEA, Vienna, 1987), 318 II p.157.
[Callen92] J.D. Callen and J.P.
Wang, Phys. Fluids B. Plasma Phyiscs 4
1139 (1992)
[Campbell88] D. J. Campbell et al, Phys Rev Lett 60 2148 (1988)
[Caramana91] E. J. Caramana, J. Comput. Phys. 96, 484 (1991).].
[Carrera86] R. Carrera, R.D.
Hazeltine, M.Kotschenreuther Phys Fluids 29
899 (1986)
[Charlton86] L. A. Charlton, J. A.
Holmes, H. R. Hicks, V. E. Lynch, and B. A. Carreras, J. Comp. Phys. 63, 107
(1986).
[Chapman39] S. Chapman and
T. G. Cowling, The Mathematical Theory of
Non-uniform Gases, Cambridge Univ. Press, Cambridge (1939).
[Chance97] M. Chance, Physics of
Plasmas 4 2161 (1997)
[Chang92] Z. Chang and J.D.
Callen, Phys. Fluids B 4 1167 (1992)
[Chang95] Z.Chang et al., Phys.
Rev. Lett. 74, 4663 (1995)
[Cheng84] C.Z. Cheng, et al. Ann.
Physics 161 21 (1984)
[Diamond92] P.H. Diamond, P.L.
Similon, T.C.Hender,et al,Phys. Fluids 28,1116 (1985)
[Coppi88] B. Coppi and F.
Porcelli, Fusion Technology 13 (1988) 447
[Coppi00] B. Coppi, Bull. Am.
Phys. Soc. 45 366 (2000)
[Forest96] C.Forest, M.Ono, Y.Hwang, Phys. Rev. Lett, 77 3811 (1996)
[Fu95] G.Y. Fu and W.Park, Phys.Rev.Lett, 74 1594 (195)
[Furth63] H.P. Furth, J. Killeen, M.N.Rosenbluth Phys. Fluids 6 459 (1963)
[Garabedian96] P.R. Garabedian, Physics of Plasmas 3 2483 (1996)
[Gianakon96] T.A. Gianakon ,J.D. Callen, and C.C.Hegna, Phys. Plasmas 3 4637 (1996)
[Gianakon99] T.A. Gianakon, Bull. Am. Phys. 44 Soc. Paper CP1 116, page 82 (1999)
[Glasser99] A. H. Glasser, C. R.
Sovinec, R. A. Nebel, T. A. Gianakon, S. J. Plimpton, M. S. Chu, D. D. Schnack,
and the NIMROD Team, Plasma Phys. Control. Fusion 41, A747 (1999). Also see http://nimrodteam.org/.
[Hammett90] G. Hammett and F. W.
Perkins, Phys. Rev. Lett 64 3019 (1990)
[Harned89] D. S. Harned and Z. Mikic, J. Comput. Phys. 83, 1 (1989).
[Hazeltine87] R.D. Hazeltine et al, Phys. Fluids 30
3204 (1987)
[Hazeltine92] R.D. Hazeltine and
J.D. Meiss, Plasma Confinement
(Addison-Wesley, The Advanced Book Program, Redwood City, CA, 1992)
[Held01]E. D. Held, J. D. Callen, C. C. Hegna and C. R. Sovinec, “Conductive electron heat flow along magnetic field lines”, to appear in Physics of Plasmas, April 2001.]
[Hirshman81] S.P.Hirshman and D. J. Sigmar, Nucl. Fusion 9, 1079 (1981)
[Jardin97] S. C. Jardin, C.E. Kessel, et al , Fus. Eng. And Design 38 27 (1997)
[Lee88] W.Lee and W.Tang, Phys. Fluids, 31 612 (1988)
[Lerbinger91] K. Lerbinger and J.
F. Luciani, J. Comp. Phys. 97
(1991).
[Lin00] Z.Lin, M.S.Chance,
T.S.Hahm, et al, Nucl. Fus. 40 737 (2000)
[Lionello99] R. Lionello, Z. Mikic, and J. A. Linker, J. Comput. Phys. 152, 346(1999).
[mdsplus01] see
www.psfc.mit.edu/mdsplus
[Meade99] D.M.Meade, et al., PPPL-3307, Princeton Plasma Physics Laboratory, (1999)
[Nebel94] R.A.Nebel, D.C.Barnes, and W.D. Nystrom,
“Three-dimensional Calculations Using the Quiet Implicit PIC Method” Bull. Am.
Phys. Soc 39 1725 (1994)
[Okabayashi98] M. Okabayashi, N.
Pomphrey, R. Hatcher, Nucl Fus 38
1607 (1998)
[Ono00] M.Ono, D.Gates, R.Ewig, et
al Nuclear Fusion 40 557 (2000)
[Orszag71] S. Orszag, J. Fluid
Mech 49, 75 (1971)
[Park86] W.Park, D. Monticello, H. Strauss, et al, Phys.
Fluids, 29, 1171 (1986)
[Park92] W.Park, S.E. Parker, M.Chance et al, Phys. Fluids B
4 2033 (1992)
[Park95] W. Park, E. Fredrickson,
A. Janos, et al., Phys. Rev. Lett. 75,
1763 (1995).
[Park99] W.Park, E. Belova, G.Fu 6
1796 (1999)
[Parker93] S.Parker and W.Lee,
Phys. Fluids B 5, 77 (1993)
[Plimpton99][S. J. Plimpton, C. R. Sovinec, T. A. Gianakon, S. E. Parker, and the NIMROD Team, "Recent Algorithmic and Computational Efficiency Improvements in the NIMROD Code," BAPS 44, 82 (1999).].
[Rogers95] B.Rogers and L.Zakharov, Physics of Plasmas, 2 3420 (1995)
[Schnack87] D. D. Schnack, D. C.
Barnes, Z. Mikic, D. S. Harned, and E. J. Caramana, J. Comp. Phys. 70, 330 (1987).
[Simonen91] T.C. Simonen, Journal
of Fusion Energy, 10 263 (1991)
[Sovinec01] C. R. Sovinec, J. M.
Finn, and D. del-Castillo-Negrete, Phys. Plasmas 8, 475 (2001)
[Sovinec98] C. R. Sovinec, R. A.
Nebel, and D. D. Schnack, “Toroidal geometry effects in the reversed-field
pinch MHD dynamo,” Bull. APS 43,
1718 (1998).
[Sovinec01] C.R. Sovinec, J.M.
Finn, et. al. Phys. Plasmas 8, 475
(2001)
[Strauss96],"Edge-Localized Mode Simulations in Divertor
Tokamaks,"Phys.Plasma 3,
4095(1996)
[Strauss98] H. Strauss and W.Park, Phys. Plasmas 5, 2676 (1998)
[Sugiyama00] L. Sugiyama and W. Park, Phys. of Plasmas 7 (2000) 4644., L.E. Sugiyama, W. Park, H.R. Strauss, et al., Nucl. Fusion (2001) to appear.
[VonGoeler74] S. Von Goeler, W.
Stodiek, and N. Sauthoff, Phys. Rev. Lett 33
1201(1974)
[Ward94] D. J. Ward and A.
Bondeson, Phys. Rev. Lett 72 2709
(1994)
[Zakharov92] L.Zakharov, et al.,
Phys. Fluids B 4 3285 (1994) F. Levinton, et al., Phys. Rev. Lett. 72
2895 (1994)
Budget and Budget Explanation
INSTITUTION YEAR 1 YEAR 2 YEAR 3
1. Utah State Univ $ 83K $103K $110K
2. Univ. of Wisconsin $143K $159K $183K
3. LANL $ 50K $ 52K $ 55K
4. SAIC $200K $210k $220K
5. Univ. of Colorado $ 98K $103K $108K
6. MIT $ 90K $ 95K $100K
7. NYU $ 120K $120K $125K
8. PPPL $ 166K $252K $265K
9. GA $ 50K $ 53K $ 56K
TOTAL $1000K $1147K
$1222K
Personnel and Tasks:
1. Utah State
University
Years 1,2,3: 100% post-doc salary (new hire)
Years 2,3: 17% Eric Held salary
The analytical and numerical aspects of the proposed improvements and implementation of the Chapman-Enskog-like closures
2. University of
Wisconsin
Years 1,2,3: 100% graduate student salary (new hire)
100% post-doc salary (new hire)
12% Carl Sovinec salary
20% system administrator salary (new hire)
Plus travel and computer expenses
Algorithm development and applications.
3. Los Alamos
National Laboratory (LANL)
Years 1,2,3: 15% Rick Nebel salary Plus travel and computer expenses
Implement realistic boundary conditions. Neo-classical closures. Applications to tokamaks. Improved implicit formulation. Two-fluid formulation.
4. Science Applications International Corp.
(SAIC)
Years 1,2,3: 100% staff scientist (new hire) Plus travel and computer expenses
Implement realistic boundary conditions. Improved implicit formulation. Analytic and particle closures. Applications to tokamaks and stellarators.
5. University of Colorado
Years 1,2,3: 100% post-doc salary (new hire), part-time support for a Graduate Research Assistant, associated travel and computer expenses.
Formulation of evolving Maxwellian df closures. Development of unstructured grid df particle-in-cell methods.
6. Massachusetts Institute of Technology
Years 1,2,3: 100% post-doc salary (new hire) plus travel
Formulate, implement, test, and apply two-fluid MHD in M3D
7. New York University
Years 1,2,3: 100% post-doc salary (new hire) plus travel
Mesh related development and problems, field line following, adaptive refinement, interface with Glimm's effort, Stellarator applications
8. Princeton Plasma Physics Laboratory
Year 1 6 months post-doc salary Years 2,3: 100% post-doc salary (new hire)
Implement parallel particle following algorithms and applications
Year 1,2,3: 25% Scott Klasky for development of advanced visualization 15% Steve Jardin for interfacing with CSET partners, reviews, coordination, meetings, applications
9. General Atomics
Years 1,2,3 30-35% of a data-management person to develop storage/vis system for both NIMROD and M3D
[Note: detailed institutional budget pages are given in Appendix D]
Other Support of Investigators
Dalton Schnack:
Agency Grant No. Value/Year Period %time
DOE/OFES DE-FG03-91ER54124 $295K 10/98 - 9/01 50%
DOE/OFES DE-FG03-99ER54528 $195K 9/99 - 8/02 15%
Biographical Sketches:
James D. Callen
is Donald W. Kerst Professor of Engineering Physics and Physics at the University
of Wisconsin. He is director of the university's Center for Plasma Theory and
Computation. He is a co-author of two books and over 160 refereed
publications, and is heavily involved in the U.S. plasma and fusion programs,
having served on a number of Department of Energy review panels and fusion
plasma physics journal editorial boards and chaired the APS Division of Plasma
Physics (in 1996). His current plasma research includes: developing
fluid/kinetic hybrid descriptions of magnetically confined plasmas; studying
the macroscopic phenomenology caused by MHD tearing-type modes and their
effects on plasma behavior and confinement in tokamaks; and attempts to
correlate the theory of collective macroscopic instabilities, which may give
the ultimate limit on the plasma pressure and current that can be magnetically
contained, with experimental results from tokamaks, stellarators, and reversed-
field pinches. He received his PhD in 1968 in Nuclear Engineering (applied
plasma physics) from the Massachusetts Institute of Technology, held an NSF
postdoctoral fellowship at the Institite for Advanced Study (Princeton) in
1968-69, taught at MIT from 1969-1972, was a research staff member and Theory
Section Leader at ORNL 1972-1979, and has been at UW-Madison since 1979. He is
a Fellow of the American Physical Society and the American Nuclear Society, has
been awarded a Guggenheim Fellowship and is a member of the National Academy of
Engineering.
Guo-yong Fu is a Research Physicist at the Princeton
University Plasma Physics Laboratory. His main research area includes energetic
particle physics and MHD stability
of toroidal plasmas. He has authored over 60
refereed publications in plasma physics.
He received a Ph.D in physics from The University of Texas at Austin in 1988.
After a one year postdoctoral fellowship at the Institute of Fusion Studies in
Austin, Texas, He worked on MHD stability in stellarators at the center for
plasma physics research (CRPP) in Lausanne, Switerland from 1989 to 1991. He
joined PPPL in 1992. He is currently active in area of MHD stability in compact
stellarators and nonlinear dynamics of energetic particle-driven fishbone and
TAE. He won the Kaul Foundation Prize for excellence in plasma physics research
in 1998.
Chris
C Hegna is
an associate scientist at the University of Wisconsin working in the Center for
Plasma Theory and Computation. He has worked continuously in the field of
theoretical plasma physics since the completion of his doctoral studies at Columbia
University in 1989. His research interests
are in the areas of magnetohydrodynamic equilibrium and stability, transport
properties of plasmas, and general magnetic confinement theory employing
analytic and computation techniques to study plasma dynamics. He has authored
or co-authored more than 55 publications in refereed plasma physics
journals. Following a one year post
doctoral position with Columbia University working at the Princeton Plasma
Physics Laboratory, he has been at
Wisconsin playing a central role in advising
and directing doctoral and post doctoral studies of several plasma
theory students. He has been actively
involved in providing theoretical support to the three major experimental confinement
programs at Wisconsin. He is active in the domestic and international magnetic
confinement communities where he has been involved in scientific collaborations
with several prominent research laboratories.
Eric D. Held is an assistant
professor of physics at Utah State University (USU). Dr. Held is intent on developing a vibrant fusion theory group at
USU capable of contributing to the U. S. fusion effort both from an analytical
and a numerical perspective. His PhD
thesis (University of Wisconsin) and subsequent work on parallel electron heat
flow has been described as "innovative, physically insightful and
thorough" research on a "frontier theoretical and computational
plasma physics issue." Dr. Held
was a participant in DOE's prestigious Computational Science Graduate
Fellowship program and has also completed a successful post-doctoral research
appointment at Los Alamos National Lab (LANL) under the auspices of DOE's
Fusion Energy Postdoctoral Research Program.
While at LANL, Dr. Held's investigation of electron heat transport along
chaotic magnetic field lines yielded the novel result of electron heat flowing
against local temperature gradients in nearly collisionless plasmas. Dr. Held is an expert on the analytical
derivation and numerical implementation of general, analytic closure relations
for nearly collisionless plasmas.
Stephen
C. Jardin
is a Principal Research Physicist at the Princeton University Plasma Physics
Laboratory. He is presently Co-Head of
the Computational Plasma Physics Group at PPPL, Head of the Next Step Options
Physics, and Theory Department MHD Coordinator. He has been Lecturer with Rank of Professor in the Princeton
University Astrophysics Department since 1986.
He holds a BS in Engineering Physics from the University of California,
a MS (Physics) and MS (Nuclear Engineering) from MIT, and a PhD in Astrophysics
from Princeton University (1976). He
was the primary developer of several widely used MHD equilibrium, stability,
and transport codes including the Tokamak Simulation Code (TSC). He holds 4 US patents, has had over 150
refereed publications in plasma physics, and has supervised 6 Princeton
University PhD students. He is a member
of Phi Beta Kappa and a Fellow of the American Physical Society. He has held key positions in several fusion
device design teams including those for S-1, PBX-M, CIT, BPX, TPX, ARIES, and
ITER. He is presently a member of the
NERSC Executive Committee Users Group, the ESNET Steering Committee, and is
Chair of the NERSC Program Advisory Committee and of the National Transport
Code Collaboration (NTCC) Program Advisory Committee.
Richard A. Nebel
is a recognized expert on Magnetohydrodynamic simulations and in particular its
application to Reversed-Field Pinch (RFP) fusion devices. He has 20 years experience with large-scale
computation and 37 refereed articles in the field. He played an instrumental role in uncovering the relaxation
mechanism that is observed in the RFP device.
His present research interests include Electrostatic Confinement fusion
and 3-D two-fluid effects effects in RFPs and tokamaks. Dr. Nebel received his B.S. degree as a
James Scholar at the University of Illinois in 1975. He then started graduate school in Nuclear Engineering as an ERDA
Trainee followed by a year as a University Fellow. He received his PhD in 1980.
He then went to Los Alamos National Laboratory as a Director's
Post-Doc. In 1982, he joined the staff
of the magnetic fusion plasma theory group (CTR-6) as a staff member. In 1990, Dr. Nebel was promoted to Section
Leader for Plasma Theory in Group CTR-7.
He served in that post supervising eight Ph.D. physicists until the
demise of CTR division in 1991. He then
became a staff member in the Theoretical Division. From 1993-1995, Dr. Nebel served as group leader for the Plasma
Theory group, T-15. In 1995, he stepped
down to return to research. Dr. Nebel’s
most recent accomplishment is that he successfully designed, built and operated
a plasma/fusion based neutron source for Safeguards applications.
Wonchull Park is a Principal
Research Physicist at the Princeton University Plasma Physics Laboratory. He
has a Ph.D from Columbia University, and is a Fellow of American Physical Society.
His primary field of research is 3D numerical simulation studies of plasmas,
using multilevel physics models, MHD, Two-fluids, and various Particle/Fluid
hybrid models. He has authored or coauthored over 100 refereed
publications in plasma physics
Scott E. Parker
is an Assistant Professor in the Department of Physics at the University of Colorado,
Boulder. His research interests are in
large-scale kinetic simulation of low-frequency plasma physics with 24 refereed
publications in this area. He received his B.S. in Nuclear Engineering and
Mathematics from the University of Wisconsin, Madison in 1985 and his Ph.D. in
Engineering Science from the University of California, Berkeley in 1990. From 1990-1996 he was a Staff Research
Physicist in the Theoretical Division at the Princeton Plasma Physics Laboratory.
He received the DOE Junior Faculty
Development Award in 1997, a DOE Fusion Postdoctoral Fellowship in 1990, a
Kaiser Engineers Quadrex Fellowship and a University of California Regents
Fellowship in 1985. In 1997 he was
leader of the Cyclone Team, a DOE initiative to study the physics basis of
transport predictions for ITER.
Dalton Schnack is a
computational physicist with over 30 years experience in the analytic and
numerical solution of nonlinear, multidimensional problems in hydrodynamics and
magnetohydrodynamics (MHD). He has
authored or co-authored many papers in the fields of linear and nonlinear
resistive MHD, and computational methods related to such problems. He has extensive experience in the
supercomputing environment. He is
actively involved in studying the nonlinear MHD properties magnetic fusion
experiments and the solar corona, and in the highly nonlinear (turbulent)
properties of the Navier-Stokes and MHD equations. After receiving his B.S., Dr. Schnack worked for over seven
years (1967-1973) for the Pratt and Whitney Division of United Technologies
Corporation as a Senior Scientific Programmer/Analyst. There he worked on computational
problems of steady flow in nozzles and supersonic exhaust jets, and the
performance of axisymmetric compressors.
During this time he completed work on an M.S. in physics, which included
a thesis on ultrashort optical pulse propagation. Dr. Schnack did his doctoral
research at Lawrence Livermore Laboratory under Prof. John Killeen where he
began his interest in nonlinear MHD processes in fusion plasmas. After
graduation he served as a staff physicist in the computational physics group at
the National Magnetic Fusion Energy (MFE) Computer Center, a supercomputer
network funded by the Department of Energy.
In 1980 he joined the fusion theory group at Los Alamos National
Laboratory where he worked on problems relevant to the reversed-field pinch and
compact torus experiments. In July 1982 Dr. Schnack joined the Applied Plasma
Physics and Technology Division of SAIC, and in 1996 was appointed Director of
the Center for Energy and Space Science.
He is presently Principal Investigator for two grants with the U. S.
Department of Energy. He is actively
involved in research related to the nonlinear fluid dynamics of advanced
magnetic fusion devices, and the nonlinear properties of the MHD
equations. Dr. Schnack is a member of
Phi Kappa Phi, national scholastic honor society, and is a Fellow of the
American Physical Society. He is also a
member of the American Geophysical Union and the Solar Physics Division of the
American Astronomical Society He has
been an active participant in the functions of the international fusion program
for many years. Dr. Schnack has
co-authored over 70 refereed publications, and 1 book.
David
Schissel is
a principal scientist and manager of the Data Analysis Applications Group at
the DIII-D National Fusion Facility. He received a B.S. in Nuclear Engineering
from the University of Wisconsin in 1979 and an S.M in Plasma Physics from the
Massachusetts Institute of Technology in 1982. He is responsible for
coordinating computer hardware and software resources to support the DIII-D
scientific staff's data analysis requirements. Data analysis support work has
included implementing advanced Unix based CPU load balancing, implementing a
100baseT network, enhanced data management and storage, large GUI based
analysis tools, and advanced scientific visualization with IDL, VTK, and
OpenGL. He is the first author on 20
articles in major scientific journals, has contributed significantly to 41 others, has participated
in numerous international conferences,
and has presented invited lectures in the United States, Europe, Japan, and the
former Soviet Union. He is a Fellow of the American Physical Society.
Carl
R. Sovinec is presently a Technical Staff Member in the
Plasma Theory Group of Los Alamos National Laboratory and will be an Assistant
Professor of Engineering Physics at the University of Wisconsin-Madison
starting in July 2001. His research interests
lie in computational plasma physics and magnetohydrodynamics, and the numerical
simulation of laboratory and astrophysical plasmas. He received his BS from the United States Air Force Academy in
1985, an MS in Nuclear Engineering from the University of Washington in 1987,
and a PhD in Plasma Physics from the University of Wisconsin-Madison in
1995. He served as a commissioned officer
in the regular Air Force from 1985-1991, including four years as a research
officer at the Phillips Laboratory in Albuquerque, NM.
Hank
Strauss is
a Research Professor in the Magnetofluid Dynamics Division of the Courant Institute
of Mathematical Sciences, New York University. He has a PhD from the University
of Texas. He is a fellow of the American Physical Society. He has worked in many areas of theoretical
and computational plasma physics, particularly in magnetohydrodynamics. For the
last several years, he has been highly involved in the M3D project.
Linda
E. Sugiyama
is a research scientist in the Research Laboratory of Electronics at the Massachusetts
Institute of Technology. She has worked
in many areas of the theory and numerical simulation of magnetically confined plasmas, including equilibrium,
stability, transport, auxiliary heating, and nonlinear simulation. She first proposed and, with W. Park,
developed the two-fluid MH3D-T code for axisymmetric confined plasmas, based on
the existing MH3D MHD nonlinear code developed at PPPL. These codes formed the basis of the M3D
project. She received a B.S. from the
University of Wisconsin in 1975 and a Ph.D in Applied Mathematics from the Massachusetts
Institute of Technology in 1980. Since then, she has worked at MIT, with brief sojourns at other institutions.
François
L. Waelbroeck
has been a Research Scientist at the Institute for Fusion Studies since 1994.
His primary research interests include magnetic reconnection and the effects of
flows on plasma stability. He received a B.S. from the University of Brussels
in 1983 and a Ph.D. from the University of Texas in 1988, and was a DOE
Postdoctoral Fellow at Princeton Plasma Physics Laboratory from 1989-1990. He
has co-authored a plasma physics textbook and 25 publications.
Description
of Facilities and Resources
Princeton Plasma Physics Laboratory (PPPL) is situated on the Forrestal Campus of Princeton University. The PPPL Theory and Computational Physics Division are a national resource for the plasma physics community. The laboratory maintains an open UNIX computer system, including a tiled display wall for high resolution visualization, and a suite of fully-equipped visitor offices.
The PPPL UNIX cluster contains within it two separate Beowulf clusters with fast interconnects. The Puffin cluster consists of nine dual-processor 400MHz Pentium PCs running Linux with a 100Mb Ethernet interconnect, and the Pared cluster consists of 12 dual-processor PCs with a Myrinet interconnect. In addition, PPPL scientists and their collaborators have access to a 64 processor Origin-2000 owned jointly with the Princeton University Astrophysics and Computer Science Departments. PPPL is connected via an OC3 ESNET connection to NERSC and the other fusion facilities.
The CEMM is to be a fully distributed Center, but all
participants will have access to the PPPL computer facilities, to NERSC, and to
their own local computer facilites.
Appendix A: Plasma Fluid Models
Plasma dynamics can be completely described by the evolution
of the distribution function ![]() , for each particle species a, given by each species
plasma kinetic equation, together with the self-consistent evolution of the
electric and magnetic fields, given by Maxwell's equations. In general,
solving these equations is analytically impossible and computationally impractical
in confined plasmas. One approach is to reduce
, for each particle species a, given by each species
plasma kinetic equation, together with the self-consistent evolution of the
electric and magnetic fields, given by Maxwell's equations. In general,
solving these equations is analytically impossible and computationally impractical
in confined plasmas. One approach is to reduce
the dimensionality of the problem, by multiplying the kinetic equation by successive powers of the particle velocity v and integrating over velocity space. If the underlying distribution functions have nice properties, such as a close-to-Maxwellian velocity distribution, the resulting moment equations have fluid-like properties. They are more tractable theoretically and computationally, although formidable problems may still arise.
The magnetohydrodynamic equations (MHD) represent the simplest self-consistent limit of the moment equations. Assuming that the electrons are tied to the ions to maintain
strict local charge neutrality, the lowest order moment equations for the electron and ion species can be added together to form a set of equations for a single plasma fluid with a density r = (Mi ni + me ne) , fluid velocity v = (Mi ni vi + me ne ve) /( Mi ni + me ne) and pressure p = pi + pe. The displacement current can then be neglected in Ampere's law (since Ñ· J = 0), eliminating electromagnetic radiation and electrostatic oscillations. The MHD equations can be written in a general form, in MKS units, as
The Maxwell equations:
![]() (A-1a,b,c)
(A-1a,b,c)
The continuity equation:
![]() (A-1d)
(A-1d)
The momentum equation:
![]() (A-1e)
(A-1e)
The energy equation:
![]() (A-1f)
(A-1f)
Ohm’s law:
![]() (A-1g)
(A-1g)
The energy equation (1f) assumes that the ratio of specific heats g = ge = gi = 5/3. The MHD Ohm's law (1g) uses the fact that the electron mass is small, me/ Mi << 1 , to reduce the velocity in the term v ´ B from the ion fluid velocity vi to the MHD velocity.
In these equations, m0 is the permeability of free space, n is the number density, r is the mass density, v is the center of mass velocity, B is the magnetic flux density, E is the electric field, J is the current density, p is the scalar pressure, q is the heat flux, h
is the electrical resistivity, P = pI + P where I is the unit tensor and P is the traceless part of the stress tensor, and Q is other heat sources and sinks. In the strict MHD ordering, only a limited subset of the higher order moments appear, representing local plasma interactions.
When the electron motion decouples from the ion motion, the moment equations yield a true two-fluid system. For near-Maxwellian distribution functions, for example,
decoupling can occur due to the effects of a non-negligible ion Larmor radius (finite Larmor radius or FLR), which is still small relative to the system size. Other effects also separate the two species. Assuming quasineutrality and keeping terms of the FLR order in the higher order moments P, q , Q, and R, yields the same equations (1a)-(1f). The Ohm's law becomes the electron momentum equation. Keeping terms of order me/Mi, it is
![]() (A-2)
(A-2)
where Re is the collisional friction term for the electrons. It requires a pressure or temperature equation for the electrons,
![]() (A-3)
(A-3)
Additional detail, still within the confines of a two-fluid moment description, can be obtained by keeping the anisotropies relative to the confining magnetic field, such as the two pressures p^ and p½½ and/or the heat fluxes. The above equations then refer to the average quantities p j= (pj½½+2pj^)/3, etc.
To close the system, expressions for the higher order moments P and q must be obtained independently, from solutions to the kinetic equation. At high collisionality, these are the usual collisional viscous stress tensor and the heat flux (proportional to the local velocity and temperature gradients, respectively) [Braginskii65]. At lower collisionality or long mean free path, these terms contain nonlocal kinetic effects. Proper closure becomes a complex question that must take into account details of the confinement configuration. (In toroidal systems, these nonlocal geometrical effects have been addressed in a flux-surface-averaged sense by neoclassical theory.) Unfortunately also, in this limit there is no single, unambiguous way to define the set of “two-fluid'' or FLR terms, so that models depend upon a mixture of theoretical and practical considerations (cf. discussion of FLR models that resulted in the derivation of the 4-field model [Hazeltine87]. These and related topics will be addressed by the proposed center.
Appendix B: Collaboration Letters:
Appendix C: The Software Framework:
We are building on the software framework illustrated in Figure C1. This is a collection of codes, software packages, and data management and visualization packages that have been designed to operate together, and to interface well with the existing experimental data structure. A job typically starts with either some experimental discharge or design concept that one is seeking to simulate. The experimental data in the major fusion centers is stored using the MDSplus [mdsplus01] data management system. This data (or design concept) can also be used to construct an initial plasma equilibrium state to use as an initial condition for an investigation. The equilibrium codes EFIT (free boundary) and VMEC (fixed boundary) are part of the code framework.
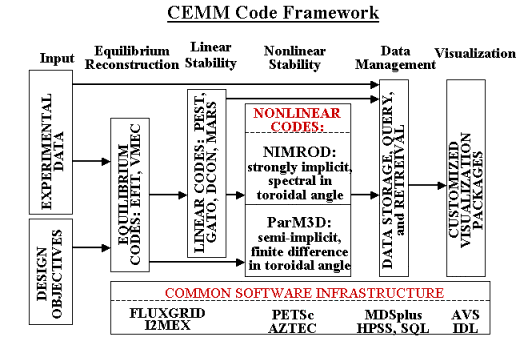
Figure C1: CEMM Code Framework developed during PSACI activity
Typically we investigate the linear stability properties of these equilibrium using one of several existing linear stability codes: GATO, PEST, or DCON for ideal stability and MARS or PEST-III for resistive stability. Equilibrium that are linearly unstable can be analyzed with either one of the nonlinear Extended MHD codes NIMROD or ParM3D. The output of these codes is saved in a MDSplus data base, very similar to what is used to store the experimental data. We have developed customized visualization packages to view either the experimental or simulation data from either of the nonlinear codes, and are developing packages to perform critical comparisons of the nonlinear data. These codes make use of software infrastructure including that developed in the fusion program (FLUXGRID and I2MEX MDSplus) for accessing equilibrium data and storing and retrieving experimental and simulation data, that developed within the DOE complex (PETSc and AZTEC) for parallel linear algebra solvers, and commercial software (HPSS, SQL, AVS, IDL) for data storage and visualization support.
Appendix
D: Institutional Budget Pages
Appendix E: Deployment Tables
The deployment of the CEMM staff is illustrated in Tables I, II, and III. Table I shows attributes of a computational model that are required for addressing important macroscopic issues in fusion physics. Table II shows the specific tasks that must be performed to successfully implement the required attributes. Table III shows the distribution of manpower within CEMM to assure that these technical attributes will be successfully incorporated. Together, these tables provide a functional mapping from physics problems to CEMM personnel that assures that the technical program proposed here will be successfully completed.
TABLE
I
APPLICATIONS VS. REQUIREMENTS
|
|
Tokamaks |
Alternative Concept
Relaxation |
Stellarator |
Space Plasmas |
|||
|
Advanced Tokamaks |
Burning Plasma |
Spherical Tokamak |
RFP dynamo |
Spheromak |
|||
|
Realistic Geom. |
l |
|
l |
|
l |
l |
|
|
Extended MHD |
l |
l |
l |
l |
|
|
l |
|
Energetic Particles |
l |
l |
|
|
|
|
l |
|
Long Time Scales |
l |
l |
l |
l |
l |
l |
l |
|
Realistic Parameters |
l |
l |
l |
l |
l |
l |
l |
|
Non-ideal B. C. |
l |
|
l |
l |
|
|
|
|
Analysis and Visualization
of Results |
l |
l |
l |
l |
l |
l |
l |
TABLE II
REQUIREMENTS VS. TASKS
|
|
Realistic Geom. |
Extended MHD |
Energetic Particles |
Long-Time Scales |
Real Param. |
Non-ideal B. C. |
Analysis |
|
Closure Model |
|
l |
l |
|
|
|
|
|
Closure Coding |
|
l |
l |
|
|
|
|
|
df – Algorithm |
|
l |
l |
|
|
|
|
|
Non-axisym geometry |
l |
|
|
|
|
|
|
|
2-Fluid Algorithm |
|
l |
|
l |
l |
|
|
|
Improved Algorithm |
|
l |
l |
l |
l |
|
|
|
Vacuum and Moving Separatrix |
l |
|
|
l |
l |
l |
l |
|
Resistive Wall. B. C. |
l |
|
|
l |
l |
l |
l |
|
Develop Vis. Tools |
|
|
|
|
|
|
l |
|
Inter-face with MDS+ |
|
|
|
|
|
|
l |
|
Grids and spatial rep. |
l |
|
|
|
l |
|
|
|
Validate |
l |
l |
l |
l |
l |
l |
l |
|
Run Apps. |
l |
l |
l |
l |
l |
l |
l |
TABLE III
TASKS VS. PERSONNEL
|
|
Closure
Model |
Closure
Code |
df Algs |
Non
Axi-sym,. |
2-fluid
Algs. |
Improve
Algs |
Vis
Tool |
MDS+ |
Grids & Saptial Rep |
R.
Wall. B.C. |
Vac/Sep. |
Validation |
Run
Appls. |
|
Sovinec[1] |
|
|
|
|
l |
l |
|
|
l |
|
|
l |
l |
|
UW postdoc1 |
|
l |
|
|
l |
l |
|
|
l |
|
|
l |
l |
|
UW grad. student1 |
|
|
|
|
|
l |
|
|
|
|
|
|
l |
|
Hegna |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
Held1 |
l |
l |
|
|
|
|
|
|
|
|
|
|
|
|
USU grad. student1 |
l |
l |
|
|
|
|
|
|
|
|
|
l |
l |
|
Callen |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
Nebel1 |
|
|
|
|
l |
|
|
|
|
|
|
l |
l |
|
Gianakon |
l |
l |
|
|
|
|
|
|
|
l |
|
l |
l |
|
Parker |
|
l |
l |
|
|
l |
l |
|
|
|
|
l |
l |
|
CU postdoc1 |
|
|
l |
|
|
l |
l |
|
|
|
|
l |
l |
|
Schnack |
|
|
|
|
|
|
|
|
|
|
|
l |
l |
|
Kruger |
l |
|
|
|
|
l |
l |
l |
|
|
l |
l |
l |
|
SAIC hire1 |
|
l |
|
|
|
l |
|
|
|
|
l |
l |
l |
|
Waelbroeck |
l |
|
|
|
l |
|
|
|
|
|
|
l |
l |
|
Park |
|
|
l |
|
|
|
|
|
|
|
|
l |
l |
|
PPPL postdoc1 |
l |
|
l |
|
|
|
|
|
|
|
|
l |
l |
|
Strauss |
|
|
|
l |
|
|
l |
|
l |
|
|
|
l |
|
NYU postdoc1 |
|
|
|
l |
|
|
|
|
l |
|
|
|
l |
|
Sugiyama |
|
|
|
|
l |
|
|
|
|
|
|
|
l |
|
MIT postdoc1 |
|
|
|
|
l |
|
|
|
|
|
|
|
l |
|
Jardin1 |
|
|
|
|
|
|
|
|
|
l |
l |
l |
l |
|
Klasky1 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
G. Fu |
|
|
l |
l |
|
|
|
|
|
|
|
l |
l |
|
Tang |
|
|
l |
|
|
l |
|
|
l |
|
|
l |
l |
|
GA support1 |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
CSET TOPS partners |
|
|
|
|
|
l |
|
l |
l |
|
|
|
|
|
CSET TSTT partners |
|
|
|
|
|
l |
|
l |
l |
|
|
|
|