Appendix A: The use of X/Y coordinates in NCAR Graphics

   Previous chapter          LLUs Home          Next chapter          Index

Introduction

This appendix is intended to clear up some of the confusion about the way in which X/Y coordinates used in calls to NCAR Graphics routines are mapped to a graphics device and to collect in one place general information about the subject. It will not cover all of the details of every routine mentioned. This is one of the most difficult areas for novice users of NCAR Graphics; even experienced users sometimes have difficulties.

For historical reasons, the situation is a bit complicated (but not as complicated as one might think). Four or five different coordinate systems are mentioned in the documentation (actually, one of these now accounts for almost all of the usage). Some of the higher-level utilities change parameters that affect the mapping of coordinates used in subsequent calls; there are good reasons for this, but the documentation does not always make it clear what is going on.

Required abstractions: Plotter frame, world and user coordinates

Each graphics device uses a highly specific coordinate system; for example, the device on which I am typing now, when used in graphics mode, requires integer X coordinates ranging from 0 at the left edge of the screen to 1152 at the right edge of the screen and integer Y coordinates ranging from 0 at the top of the screen to 900 at the bottom of the screen. It would be most annoying if, every time I drew a picture, I had to use X and Y coordinates in these ranges. Therefore, two simplifying abstractions are introduced.

First, the NCAR Graphics user assumes that he or she is working with an idealized graphics device having a square display area (often referred to in the documentation as the "plotter frame"). This display area may be addressed using what are called "normalized device coordinates" (NDCs); these are X/Y coordinate pairs having the following characteristics: The X coordinate is a real number between zero and one; zero refers to the left edge of the area and one refers to the right edge of the area. The Y coordinate is also a real number between zero and one; zero refers to the bottom edge of the area and one refers to the top edge of the area. The way in which normalized device coordinates are mapped to the actual coordinates required by a given device is outside the scope of this document; typically, it is determined by the translator being used to drive the device and the "graphcap" which describes the graphical capabilities of that device.

Second, although one can work directly with normalized device coordinates (and may sometimes want to do so), this is not usually done. One works instead with what are called "world coordinates" (in the case of a few of the routines in GKS proper) or with what are called "user coordinates" (in the case of almost all other NCAR Graphics routines). Both of these are Cartesian coordinate systems using real numbers.

The way in which world coordinates and user coordinates are mapped into normalized device coordinates is controlled by the user (within limits) and is the subject of this document. The overall effect is to allow the user to work in a natural coordinate system (perhaps, for example, the system in which the data are given); NCAR Graphics routines called transform the coordinates used into the appropriate normalized device coordinates.

X/Y coordinates in calls to GKS routines (world coordinates)

Figure 1 shows how world coordinates in calls to GKS routines are mapped to the plotter frame. The mapping of world coordinates is defined by the current "normalization transformation." Each normalization transformation is associated with a nonnegative integer; currently, the NCAR Graphics GKS package only allows the use of normalization transformations 0 and 1.

To define the normalization transformation associated with an integer greater than 0, call the GKS routine GSVP to define its "viewport" and the GKS routine GSWN to define its "window." The viewport is defined by four real numbers between 0 and 1, specifying the rectangular portion of the plotter frame that is to be used; the window is defined by four real numbers, specifying a rectangular portion of the "world coordinate system" that is to be linearly mapped to the viewport. Both sets of numbers are in the order "Xmin, Xmax, Ymin, Ymax," where Xmin is less than Xmax and Ymin is less than Ymax.

Normalization transformation 0 cannot be changed. It is the identity transformation, which maps the unit square (in which all X/Y coordinates are normalized device coordinates, between 0 and 1, inclusive) back into the unit square. Its viewport and window are both defined by the four numbers 0., 1., 0., and 1., in that order.

To make a given normalization transformation the "current" one (to "select" it), call the GKS routine GSELNT. To determine the largest usable normalization transformation number, call the GKS routine GQMNTN. To determine which normalization transformation is the current one, call the GKS routine GQCNTN. To determine the window and viewport of a given normalization transformation, call the GKS routine GQNT.

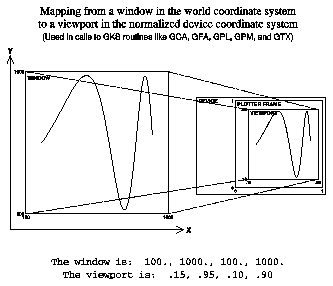
GKS routines which require the use of world coordinates include the following primitives:

GCA draws a "cell array"; it colors a rectangular area on the plotter frame, using a rectangular array of color indices provided by the caller.
GFA draws a "fill area"; it fills a polygon defined by a set of points.
GPL draws a "polyline" connecting a set of points in a given order.
GPM draws a "polymarker" marking the position of each point in a set.
GTX draws a character string at a given position.

These are the only routines the average user is likely to encounter which require world coordinates as arguments.

X/Y coordinates in calls to most NCAR Graphics routines (user coordinates)

Figure 2 shows how user coordinates are mapped to the plotter frame (for the moment, ignore references to the routine SET, which will be discussed in the next section). User coordinates are interpreted using the window and viewport of the current GKS normalization transformation, but the mapping from the window to the viewport is further modified as implied by the current values of two internal parameters, MI and LS, that provide two valuable features of the pre-GKS version of NCAR Graphics:

The parameter MI allows for "mirror imaging" (mapping increasing X values from right to left, instead of from left to right, in the viewport, or increasing Y values from top to bottom, instead of from bottom to top, in the viewport, or both).
The parameter LS allows for "log scaling" (substituting the base-10 logarithms of X and/or Y coordinates for the coordinates themselves).

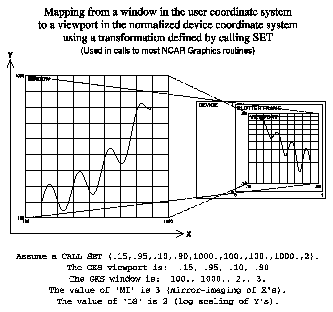
The current values of MI and LS may be set by calling the SPPS routine SETUSV and retrieved by calling the SPPS routine GETUSV. Possible values are as follows:

MI = 1 - X mapping normal, Y mapping normal (the default)
MI = 2 - X mapping normal, Y mapping inverted
MI = 3 - X mapping inverted, Y mapping normal
MI = 4 - X mapping inverted, Y mapping inverted

LS = 1 - X mapping linear, Y mapping linear (the default)
LS = 2 - X mapping linear, Y mapping logarithmic
LS = 3 - X mapping logarithmic, Y mapping linear
LS = 4 - X mapping logarithmic, Y mapping logarithmic

Example: Assume that normalization transformation 1 is the current one, that its viewport is defined by the four numbers 0., .5, .5, and 1. (which refers to the upper left quadrant of the plotter frame), and that its window is defined by the four numbers -1., 1., 0., and 2. Assuming that MI and LS have default values, the statement

    CALL POINT (0.,1.)

will draw a point in the center of the viewport (which is just what the equivalent call to the GKS routine GPM would do). Changing the value of LS to 2 would move the point drawn by POINT to the center of the bottom edge of the viewport (because the change in LS makes the Y mapping logarithmic and the base-10 logarithm of 1. is 0.). Changing the value of MI to 2 would then move the point to the center of the top edge of the viewport (because the change causes mirror-imaging of Y coordinates). A call to GPM would not be affected by the changes in LS and MI.

To repeat: X/Y coordinates in calls to GKS routines are not affected by the values of LS and MI; these routines expect world coordinates (as defined by the GKS standard), not user coordinates. The five GKS routines you are most likely to use are GCA, GFA, GPL, GPM, and GTX.

Note: Even when normalization transformation 0 is the current one, the flags LS and MI affect the interpretation of X/Y coordinates in calls to NCAR graphics routines that expect user coordinates. If your object in using normalization transformation 0 is to use normalized device coordinates in a meaningful way, then you will probably (but not necessarily) want to reset LS and MI to their default values.

The routine SET

The SPPS routine SET provides a way to set the current viewport and window and the values of the parameters MI and LS all at once. (That is to say, it allows one, with a single call, to completely define the user coordinate system.) SET is meant to have the same effect as the routine SET in the pre-GKS version of NCAR Graphics. Consider the statement

CALL SET (VPL,VPR,VPB,VPT,WDL,WDR,WDB,WDT,LLF)

VPL, VPR, VPB, and VPT are the four numbers defining the desired viewport; each of the values is between 0 and 1, inclusive; the suffixes "L", "R", "B", and "T" refer to the left, right, bottom, and top edges of the viewport, respectively. It must be the case that VPL is less than VPR and that VPB is less than VPT.

WDL, WDR, WDB, and WDT define the desired window in the user coordinate system. The desired value of the mirror-imaging parameter MI is implicit in the ordering of these values. If WDL is less than WDR, then X coordinates are not to be mirror-imaged; otherwise they are. Similarly, if WDB is less than WDT, then Y coordinates are not to be mirror-imaged; otherwise they are. Note that WDL and WDR specify a range of values of X coordinates prior to the taking of logarithms, if any, specified by LLF; similarly, WDB and WDT specify a range of values of Y coordinates prior to the taking of logarithms, if any, specified by LLF.

The final argument, LLF, specifies the desired value of the log-scaling parameter LS; its value must be one of 1, 2, 3, or 4. Note that, if the value of LLF is other than 1, then either the first two, or the last two, or all four of the numbers defining the window of the GKS normalization transformation will be base-10 logarithms of the arguments WDL, WDR, WDB, and WDT.

The routine SET always redefines normalization transformation 1 and makes it the current normalization transformation. The values of the arguments VPL, VPR, VPB, and VPT are used, in that order, to define the viewport of normalization transformation 1. The values of the arguments WPL, WPR, WPB, and WPT (or their base-10 logarithms, depending on the value of LLF) are used to define the window of normalization transformation 1; the order of these values may have been changed.

Examples: Below are shown four SET calls; each is followed by the resulting values of the GKS viewport and window and the values of the SPPS parameters MI and LS.

CALL SET ( .1, .9, .3, .7 , -1., 1., 1., 10. , 1 )

GKS viewport: .1, .9, .3, .7
GKS window: -1., 1., 1., 10.
Value of MI: 1
Value of LS: 1

CALL SET ( .1, .9, .3, .7 , 1., -1., 1., 10. , 1 )

GKS viewport: .1, .9, .3, .7
GKS window: -1., 1., 1., 10.
Value of MI: 3
Value of LS: 1

CALL SET ( .1, .9, .3, .7 , -1., 1., 1., 10. , 2 )

GKS viewport: .1, .9, .3, .7
GKS window: -1., 1., 0., 1.
Value of MI: 1
Value of LS: 2

CALL SET ( .1, .9, .3, .7 , 1., -1., 10., 1. , 2 )

GKS viewport: .1, .9, .3, .7
GKS window: -1., 1., 0., 1.
Value of MI: 4
Value of LS: 2

Note: You must remember that, when you call SET, it will affect the values of the internal parameters MI and LS. If you then call the GKS routine GSELNT to select a different normalization transformation, the parameters MI and LS will not be reset and will therefore affect the interpretation of user coordinates in subsequent calls. In particular, if you use mirror-imaging and/or log scaling and then call GSELNT to make normalization transformation 0 the current one, the mirror-imaging and/or log scaling will still be in effect unless you also reset MI and/or LS to 1 using SETUSV calls.

See also the example code and plot at the end of this document.

The routine GETSET

The SPPS routine GETSET provides a way to retrieve the nine values that, when used as arguments in a subsequent SET call, will restore the current mapping of user-system X/Y coordinates. It is called using a statement of the form

    CALL GETSET (VPL,VPR,VPB,VPT,WDL,WDR,WDB,WDT,LLF)

It is important to realize that, if the GETSET call is executed when normalization transformation 0 is the current one, a subsequent SET call using the nine returned values will not exactly restore the underlying GKS parameters; instead, it will redefine normalization transformation 1 to have the same effect as normalization transformation 0.

See also the example code and plot at the end of this document.

Other coordinate systems used in NCAR Graphics

Three other coordinate systems used in NCAR Graphics are described in the "Coordinate systems in NCAR Graphics" section of this guide, and in the User's Guide for NCAR GKS-0A Graphics programmer document. Thumbnail descriptions follow. All three of these systems are used to address points on the entire plotter frame.

The "fractional" coordinate system uses real X coordinates ranging from 0 at the left edge to 1 at the right edge and real Y coordinates ranging from 0 at the bottom edge to 1 at the top edge. These correspond to what are called "normalized device coordinates" in GKS. This system is used frequently.
The "metacode" coordinate system (PAUs) uses integer X coordinates ranging from 0 at the left edge to 32,767 at the right edge and integer Y coordinates ranging from 0 at the bottom edge to 32,767 at the top edge. This coordinate system is a relic which has not been entirely eradicated. Users should avoid using it.
The "plotter" coordinate system uses integer X coordinates ranging from 1 at the left edge to 2**MX at the right edge and integer Y coordinates ranging from 1 at the bottom edge to 2**MY at the top edge. MX and MY are the values of internal parameters that can be set using SETUSV and retrieved using GETUSV. The default values of MX and MY are 10 and 10. This coordinate system is a relic which has not been entirely eradicated. Users should avoid using it.

Each of the following SPPS routines uses one of these coordinate systems:

FL2INT, given an X/Y coordinate pair in the user system, returns an X/Y coordinate pair in the metacode system.
MXMY returns the metacode coordinates of the current pen position.
PLOTIF raises or lowers the "pen," as directed, and then moves it to a specified position in the fractional coordinate system.
PLOTIT raises or lowers the "pen," as directed, and then moves it to a specified position in the metacode coordinate system.

The fractional coordinate system is used in several high-level utilities to specify what portion of the plotter frame to use.

The 3D packages ISOSRF, ISOSRFHR, SRFACE, and THREED of course use three-dimensional coordinate systems.

Routines in the packages EZMAP and EZMAPA use latitude/longitude coordinates.

The SPPS conversion routines

SPPS provides functions to allow for easy mapping of an X or Y coordinate in one coordinate system to the corresponding X or Y coordinate in another coordinate system. A couple of them are very useful, including CFUX, CFUY, CUFX, and CUFY (the remainder are obsolete). Suppose that we wish to label a given point, whose coordinates are given in the user coordinate system, using a two-line label of the form

Xstring of information

where the "X" is to be centered on the point in question and the associated string of information is to be a little to the right of and below the X. Assume that the desired string of information is in a character variable CHRS. The code required would be something like the following:

  CALL PLCHHQ (X,Y,'X',.02,0.,0.)
  CALL PLCHHQ (CFUX(CUFX(X)+.01),CFUY(CUFY(Y)-.01),CHRS,.01,0.,-1.)

The high-quality character-writing routine PLCHHQ, from the package Plotchar, is used. In each of the first two arguments in the second call, we convert a coordinate from the user system to the fractional system, add a constant that is meaningful in the fractional system, and then convert the coordinate back into the user system.

Use of SET and GETSET by various utilities

Many of the NCAR Graphics utilities have as arguments X/Y coordinates that are expected to be in the user coordinate system, as defined by the current GKS window and viewport and the SPPS parameters MI and LS (all of which may have been defined by a call to SET, of course).

Many of the utilities themselves call SET. Some of these first save the current definition of the user coordinate system (by a call to GETSET) and then restore that definition (by another call to SET) before returning to the caller; others (intentionally) do not. Even those that do save and restore the original SET call may change the current normalization transformation number and the definition of normalization transformation number 1 (for reasons detailed in the descriptions of the routines SET and GETSET, above).

Below are listed all of the NCAR utility packages. Each is accompanied by a short description of ways in which the package makes use of X/Y coordinates in the user coordinate system and of the routines SET and GETSET. Remember that the user coordinate system may have been defined by a SET call or by the equivalent GKS calls to define the window and viewport of the current normalization transformation and the SPPS calls to define the values of the parameters MI and LS; for the sake of brevity, the phrase "the most recent SET call" will be used instead of the longer "the most recent SET call or equivalent calls to ...".

Areas:: The routines ARDRLN, AREDAM, and ARGTAI have arguments that are X/Y coordinates in the user coordinate system; these arguments are interpreted according to the most recent SET call.

The routine ARDRLN calls the user routine specified by the argument "LPR" (which is expected to examine a polyline and either draw it or ignore it) with X/Y coordinates in the fractional system; prior to each such call, ARDRLN calls SET to define the user system to be identical to the fractional system (so that the X/Y values provided will be usable in calls to any of the routines that draw polylines). Similarly, the routine ARSCAM calls the user routine specified by the argument "APR" (which is expected to examine an area and either fill it or ignore it) with X/Y coordinates in the fractional system. Again, ARSCAM calls SET to define the user system to be identical to the fractional system (so that the X/Y values provided will be usable in calls to any of the routines that do area fill. In both cases, the original SET call is saved (by calling GETSET) before the call to the user routine and restored (by another call to SET) after the call to the user routine.

Autograph:: The routines AGCURV, AGSTUP, EZY, EZXY, EZMY, EZMXY, and IDIOT have arguments that are ultimately used as X/Y coordinates in the user coordinate system. Each of these routines does a call to SET before using these coordinates.

A call to the routine AGSTUP determines the necessary SET call and does it; certain values of Autograph's internal parameter SET. may direct that some or all of the arguments in the SET call are to be obtained by calling GETSET. The routines AGBACK and AGCURV re-call SET, using arguments saved in labelled COMMON. Each of the routines EZY, EZXY, EZMY, EZMXY, and IDIOT calls AGSTUP, so each also indirectly calls SET. In no case is the original SET call saved or restored; this allows a user to draw objects on an Autograph plot using the coordinates of the data points as user coordinates.

The routine AGUTOL, which is called by Autograph and defines the mapping between the user system along a specified axis and the "label coordinate system" on that axis, may be called with an input value that is either an X or a Y coordinate in the user coordinate system. The routine AGPWRT is called by Autograph to draw character strings. User-supplied versions of these two routines may assume that X/Y coordinates defined by their arguments are commensurate with the arguments in the last SET call (which will have been done by the calling routine).

Colconv:: No arguments are X/Y coordinates in the user coordinate system.

SET is not called by Colconv.

Conpack:: Each of the routines CPRECT, CPSPS1 (also known as CPSPRS), and CPSPS2, one of which is called as the first step in drawing a contour plot, determines the SET call that will be required for subsequent drawing of the contour plot and does the necessary call. (The internal parameter SET may be given a value saying that some or all of the SET call arguments are to be obtained from a call to GETSET.) Conpack routines called subsequently that depend on the proper SET call to have been done do it for themselves, using variables saved in Conpack's labelled COMMON blocks; routines that do this are CPBACK, CPCICA, CPCLAM, CPCLDM, CPCLDR, CPCLTR, CPLBAM, CPLBDR, and CPPKLP. In no case is the original SET call saved and restored; this allows a user to draw objects on a Conpack plot using meaningful user coordinates.

X/Y coordinates used by Conpack routines to draw objects on the contour plot are user coordinates and must be commensurate with the SET call. Various desirable effects may be created (for example, the mapping of Conpack output onto an Ezmap background); creating these effects may require setting one or more of the Conpack parameters MAP, SET, VPL, VPR, VPB, VPT, VPS, WDL, WDR, WDB, WDT, XC1, XCM, YC1, and YCN. It may also require providing one's own version of the routine CPMPXY.

The routines CPCNRC and CPEZCT, which are intended to simulate the older routines CONREC and EZCNTR, do save and restore the original SET call. In this respect, they are inconsistent with the rest of Conpack, but consistent with the routines they are meant to replace.

Conran_family:: Each member of this family has as arguments arrays of X and Y coordinates which are ultimately used as X/Y coordinates in the user coordinate system. Normally, no SET call is expected to have been done by the user. Certain values of the internal parameter SCA will require a SET call to have been done.

The parameter SCA determines whether or not SET is to be called and, if so, which of the arguments are obtained by calling GETSET. If SET is called, the original SET call is not restored; this allows a user to draw objects on a plot drawn by one of these routines using meaningful user coordinates.

Dashline:: The routines FRSTD, VECTD, CURVED, LINED, and PWRTM have arguments that are X/Y coordinates in the user coordinate system; they are interpreted according to the last SET call.

No calls to SET are done by any of the routines in these packages.

Ezmap:: No arguments are X/Y coordinates in the user coordinate system.

SET is called directly by MAPINT and indirectly by MAPDRW (when it calls MAPINT). By calling MAPRS, a user may force restoration of the last SET call done by MAPINT. The fact that MAPINT calls SET allows objects to be drawn on an Ezmap background. The routines MAPFST, MAPGRD, MAPIT, MAPIQ, MAPLBL, MAPLOT, and MAPVEC all draw such objects and they all depend on the SET call to have been done by the earlier call to MAPINT. Given the latitude and longitude of a point on the globe, the routine MAPTRN allows one to retrieve an X/Y coordinate pair that is commensurate with that SET call. A call to SET that follows the call to MAPINT and precedes calls to other Ezmap routines is likely to cause problems.

The viewport to be used by Ezmap is specified by a call to MAPPOS. Typically, the map produced will not fill the entire viewport. This is because each projection has a natural aspect ratio and it is unlikely that the viewport chosen will be of exactly the shape required to hold the map specified by the call to MAPSET. To distort the map to fill a specified viewport, you can, after the call to MAPINT, insert the two statements

              CALL GETSET (XXL,XXR,XXB,XXT,WDL,WDR,WDB,WDT,LLF)

              CALL SET (VPL,VPR,VPB,VPT,WDL,WDR,WDB,WDT,LLF)

where VPL, VPR, VPB, and VPT define the desired viewport. This forces output from subsequent calls to object-drawing routines in Ezmap to fill that viewport, rather than the one defined by MAPINT.

All of the routines MAPBLA, MAPGRM, MAPIQA, MAPIQM, MAPITA, and MAPITM depend on an earlier call to MAPINT to have done a SET call. A call to SET that follows the call to MAPINT and precedes a call to one of the above routines is likely to cause problems.

Gflash:: No arguments are X/Y coordinates in the user coordinate system.

Gflash does not call SET.

Gridall:: The routines GRIDAL and HALFAX have arguments that are
X/Y coordinates in the current user coordinate system.

No routines in this package call SET. The routine GRIDAL, which may be called directly or indirectly (as a result of a call to any of the routines GRID, GRIDL, HALFAX, PERIM, or PERIML), assumes that SET has been called; it calls GETSET to obtain the values that determine where the grid is to be drawn and what labels, if any, are to be written on it.

Halftone:: No arguments are X/Y coordinates in the user coordinate system.

The argument "NPRM" determines whether or not the HAFTON routine calls SET and, if so, which of the arguments are obtained by calling GETSET. When HAFTON does call SET, it saves and restores the original SET call.

Histogram:: No arguments are X/Y coordinates in the user coordinate system.

No routines in this package call SET.

Isosurface:: No arguments are X/Y coordinates in the user coordinate system.

ISOSRF does not call SET. 3D coordinates are mapped to 2D coordinates in the metacode system and PLOTIT is called to draw the desired objects. The PWRZI routine does not call SET.

Labelbar:: No arguments are X/Y coordinates in the user coordinate system.

LBLBAR calls SET in such a way that it can work completely in the fractional coordinate system; it saves and restores the original SET call.

The routine LBFILL is called repeatedly by LBLBAR to fill the rectangles that make up the label bar; the user may supply a version of this routine to do the fill in the required manner. X/Y coordinates in calls to LBFILL are given in the fractional coordinate system; the required SET call may be assumed to have been done.

Plotchar:: PLCHHQ, PLCHMQ, and PLCHLQ have arguments that are
X/Y coordinates in the user coordinate system.

No calls to SET are done by Plotchar routines.

Scrolled_title:: No arguments are X/Y coordinates in the user coordinate system.

No calls to SET are done by the routines in this package.

Softfill:: SFSGFA and SFWRLD have arguments that are X/Y coordinates in the user coordinate system, as defined by the last SET call. These coordinates are converted to the fractional system and then passed on to the routine SFNORM.

SFNORM calls SET to make the user coordinate system identical to the fractional coordinate system; it saves and restores the original SET call.

SPPS:: The routines CURVE, FL2INT, FRSTPT, LINE, POINT, POINTS, PWRIT, VECTOR, and WTSTR have arguments that are X/Y coordinates in the user coordinate system, as defined by the last SET call.

Under certain conditions, CURVE and POINTS call SET; when they do, they save and restore the original SET call.

Streamlines:: In general, the approach Streamlines uses for coordinate system set-up is consistent with the model established by the Conpack utility.

The Streamlines initialization routine STINIT determines whether to call the SET routine based on the value of the internal parameter SET. When STINIT does the SET call, the user can influence how it is called by setting some or all of the viewport and window control parameters, VPL, VPR, VPB, VPT, VPS,WDL, WDR, WDB, and WDT. The routine that actually draws the streamlines, STREAM, assumes that the proper SET call has been performed, and, as needed, retrieves information about the current coordinate state from variables stored in Streamlines' named common blocks. Except when invoked through STRMLN or EZSTRM, interfaces that have been retained for compatibility with older versions of this utility, Streamlines does not save and restore the original SET call; this allows a user to draw objects on a Streamlines plot using meaningful user coordinates.

By default, Streamlines uses X coordinates between 1. and REAL(M) and Y coordinates between 1. and REAL(N), where M and N are the assumed sizes of the input data arrays. In other words, an identity mapping is established between the array grid boundaries and the user coordinate boundaries. By appropriately setting the parameters, XC1, XCM, YC1, and YCM, however, the user can establish a mapping from the array grid indices to a coordinate system more natural for the data, such as longitude and latitude. Moreover, when the MAP parameter has a non-default value, Streamlines can send the streamlines through a user-definable mapping transformation before arriving at user coordinate space. Two transformations are pre-defined: a mapping through the various Ezmap projections, and a polar coordinate mapping. The user may implement other mapping transformations by modifying the user-modifiable routines STUMXY, STUIXY, and STUMTA.

Internally, Streamlines maps the directional component of the streamlines using normalized device coordinates as a reference coordinate system. This is because, unlike user coordinate space, NDC space is guaranteed to be uniform and rectangular. However, the coordinates output to the drawing routines are effectively always in user coordinates. Whenever the default array grid to user coordinate space mapping is modified, either directly or indirectly, the user needs to ensure that the coordinate system boundaries align across the transformation.

The parameter, TRT, only implemented for certain settings of the MAP parameter, allows the user to control mapping of the directional component of the streamline. Depending on the value of TRT, the user can choose between a space mapping, where the directional component transforms, and a location mapping, where the mapping simply establishes the position of the grid points on an underlying rectangular coordinate system.

Surface:: No arguments are X/Y coordinates in the user coordinate system. The PWRSZ routine calls SET; it saves and restores the original SET call.

SRFACE calls SET; it saves and restores the original SET call.

Threed:: No arguments are X/Y coordinates in the user coordinate system.

POINT3 calls SET; it saves and restores the original SET call. Other routines in this package do not call SET; 3D coordinates are mapped to 2D coordinates in the metacode system, and PLOTIT is called to draw the desired objects.

Vectors:: In general, the approach Vectors uses for coordinate system set-up is consistent with the model established by the Conpack utility.

The Vectors initialization routine VVINIT determines whether to call the SET routine based on the value of the internal parameter SET. When VVINIT does the SET call, the user can influence how it is called by setting some or all of the viewport and window control parameters, VPL, VPR, VPB, VPT, VPS, WDL, WDR, WDB, and WDT. The routine that actually draws the vectors, VVECTR, assumes that the proper SET call has been performed, and, as needed, retrieves information about the current coordinate state from variables stored in Vectors' named common blocks. Except when invoked through VELVCT, VELVEC, or EZVEC, interfaces that have been retained for compatibility with older versions of this utility, Vectors does not save and restore the original SET call; this allows a user to draw objects on a Vectors plot using meaningful user coordinates.

By default, Vectors uses X coordinates between 1. and REAL(M) and Y coordinates between 1. and REAL(N), where M and N are the assumed sizes of the input data arrays. In other words, an identity mapping is established between the array grid boundaries and the user coordinate boundaries. By appropriately setting the parameters, XC1, XCM, YC1, and YCM, however, the user can establish a mapping from the array grid indices to a coordinate system more natural for the data, such as longitude and latitude. Moreover, when the MAP parameter has a non-default value, Vectors can send the vectors through a user-definable mapping transformation before arriving at user coordinate space. Two transformations are pre-defined: a mapping through the various Ezmap projections, and a polar coordinate mapping. The user may implement other mapping transformations by modifying the user-modifiable routine, VVUMXY.

Internally, Vectors maps the directional component of the vectors using normalized device coordinates as a reference coordinate system. This is because, unlike user coordinate space, NDC space is guaranteed to be uniform and rectangular. However, the coordinates output to the drawing routines are effectively always in user coordinates. Whenever the default array grid to user coordinate space mapping is modified, either directly or indirectly, the user needs to ensure that the coordinate system boundaries align across the transformation.

The parameter TRT, only implemented for certain settings of the MAP parameter, allows the user to control mapping of the directional component of the vectors. Depending on the value of TRT, the user can choose between a space mapping, where the directional component transforms, and a location mapping, where the mapping simply establishes the position of the grid points on an underlying rectangular coordinate system.

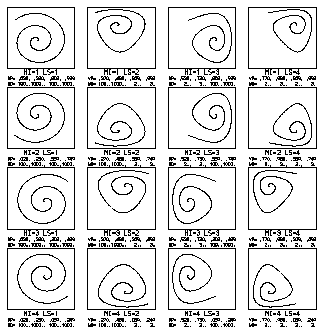
An example illustrating the effects of MI and LS

The following example illustrates the effect of MI and LS on the mapping of
X/Y coordinates from a window in the user coordinate system to a viewport on the plotter frame. Both the code and the resulting plot are given.

The plot shows a 4x4 array of rectangles, each containing a spiral drawn by a call to the NCAR Graphics routine CURVE. All the spirals are defined by the same set of X/Y coordinates in the user coordinate system. The value of the SPPS parameter MI varies from row to row and the value of the SPPS parameter LS varies from column to column, so that all possible combinations of the two parameters are shown.

The mapping for each of the sixteen curves is specified by a SET call which defines the desired viewport (in the fractional coordinate system), the desired window (in the user coordinate system), and the desired value of LS; each SET call is followed by a SETUSV call defining the desired value of MI. (To define the desired value of MI using the SET call could have been done by changing the order of arguments 5-8, which define the window; we chose not to do this, but to use the combined effect of a SET call and a SETUSV call.)

Below each curve are shown the values of MI and LS used to draw that curve and the values of the parameters defining the GKS window and viewport, as obtained by a call to the GKS routine GQNT. Note that, although the values of arguments 5-8 in the SET call (which define the window in the user coordinate system) do not change, the values of the GKS parameters which define the window do change, to reflect the current value of LS.

               ============ CODE BEGINS ============
  PROGRAM EXMPLE
C
C Define arrays to hold data defining a spiral in the user coordinate
C system.
C
        DIMENSION X(476),Y(476)
C
C Define arrays to hold the numbers defining the viewport and window,
C as retrieved from GKS.
C
        DIMENSION VIEW(4),WIND(4)
C
C Define a character variable in which to construct labels.
C
        CHARACTER*26 CHRS
C
C Open GKS.  Open and activate a single metacode workstation.
C
        CALL OPNGKS
C
C Turn off clipping at the edges of the viewport (which GKS does by
C default).
C
        CALL GSCLIP (0)
C
C Define the X and Y coordinates of a spiral in the user coordinate
C system.  It lies in a rectangular region bounded by the lines
C "X=100", "X=1000", "Y=100", and "Y=1000".
C
        DO 101 I=1,476
          THETA=.031415926535898*FLOAT(I-1)
          X(I)=500.+.9*FLOAT(I-1)*COS(THETA)
          Y(I)=500.+.9*FLOAT(I-1)*SIN(THETA)
  101   CONTINUE
C
C Loop through the possible values of 'LS'.
C
        DO 103 ILS=1,4
C
C Define the fractional coordinates of the left and right edges of the
C viewport.
C
          VPL=REAL(ILS-1)/4.+.020
          VPR=REAL(ILS  )/4.-.020
C
C For each of the possible values of 'LS', loop through the possible
C values of 'MI'.
C
          DO 102 IMI=1,4
C
C Define the fractional coordinates of the bottom and top edges of the
C viewport.
C
            VPB=REAL(4-IMI)/4.+.059
            VPT=REAL(5-IMI)/4.-.001
C
C Outline the viewport.  PLOTIF expects fractional coordinates.
C
            CALL PLOTIF (VPL,VPB,0)
            CALL PLOTIF (VPR,VPB,1)
            CALL PLOTIF (VPR,VPT,1)
            CALL PLOTIF (VPL,VPT,1)
            CALL PLOTIF (VPL,VPB,1)
C
C Call SET to define the mapping from the user system to the plotter
C frame.  The SET call specifies 'MI' = 1 (since the value of argument
C 5 is less than that of argument 6 and the value of argument 7 is less
C that of argument 8).  The SETUSV call overrides this to obtain the
C desired value.
C
            CALL SET    (VPL,VPR,VPB,VPT,100.,1000.,100.,1000.,ILS)
            CALL SETUSV ('MI (MIRROR IMAGING FLAG)',IMI)
C
C Call the routine CURVE to draw the spiral.
C
            CALL CURVE  (X,Y,476)
C
C Label the curve.  First, write the values of 'MI' and 'LS'.  Note
C the use of CFUX and CFUY to map meaningful fractional coordinates
C to the user coordinates required by PLCHMQ.
C
            WRITE (CHRS,'(''MI='',I1,'' LS='',I1)') IMI,ILS
            CALL PLCHMQ (CFUX(.5*(VPL+VPR)),CFUY(VPB-.0120),
     +                                 CHRS(1:9),.012,0.,0.)
C
C Retrieve the values defining the window and viewport, using GKS
C calls.
C
            CALL GQNT (1,IERR,WIND,VIEW)
C
C Write them out, too.
C
            WRITE (CHRS,'(''VP='',F5.3,3('','',F5.3))') (VIEW(I),I=1,4)
            CHRS( 4: 4)=' '
            CHRS(10:10)=' '
            CHRS(16:16)=' '
            CHRS(22:22)=' '
            CALL PLCHMQ (CFUX(.5*(VPL+VPR)),CFUY(VPB-.0320),
     +                                CHRS(1:26),.008,0.,0.)
            WRITE (CHRS,'(''WD='',F5.0,3('','',F5.0))') (WIND(I),I=1,4)
            CALL PLCHMQ (CFUX(.5*(VPL+VPR)),CFUY(VPB-.0480),
     +                                CHRS(1:26),.008,0.,0.)
C
C End of loop through the values of 'MI'.
C
  102     CONTINUE
C
C End of loop through the values of 'LS'.
C
  103   CONTINUE
C
C Terminate GKS.
C
        CALL CLSGKS
C
C Done.
C
        STOP
C
      END
             ============= CODE ENDS =============

   Previous chapter          LLUs Home          Next chapter          Index