Balloon takes the two input data mapout and mapdsk from Mapck.
It is available through lmhd svn repository
svn+ssh://svnsrv.pppl.gov/svn/mhd/trunk/Balloon.
The syntax is
Balloon
It also needs the input file balin to run.
The preallocated fixed array sizes are given in balmp.i
parameter(ns0=401,nt0=256,nq=526,ny=526,ns=ns0+1,nt=nt0+5)
c.....nsf0 is number of psi surfaces
parameter(nsf0=401)
c.....nths0 is number of theta points
parameter(nths0=256)
c.....nths is maximum array dimension for theta points
parameter(nths=nths0+5)
c.....nsf is maximum array dimension for psi surfaces
parameter(nsf=nsf0+1)
in which nsf ≡ ns and nths ≡ nt defined in maplst.
The actual size are
nosurf= 201 and mth= 128
which should be matched in the input file
balin:
∧ inp
ndist=2,201,3, thpi=24., lzio=1, lljin=1, s=1.0
∧ end
balmc.i: common / equ5 / ntitle(20), dat, nx, nz, nosurf, mth, lpless,
balmsch_copy.f
70 call zrd ( iomode,ntitle(1),nsiz,nadres,lgivup,100 )
76 write(*,*) nx, nz, nosurf, mth, lpless
128 129 201 128 F
| | | |
| | +---+-> get from mapck
+---+-> get from Jsolver through mapck
balin:
ndist=2,201,3: the flux surfaces chosen to be analyzed are 2, 5, 8, 11, ..., 201
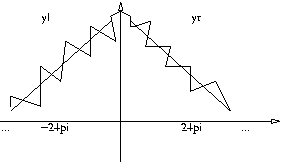
thpi=24. : integration range in ballooning coordinate, theta, here example [-24pi, 24pi],
eigenvector is yl on [-24pi, 0] and yr on [0, 24pi], matched at 0.
lljin=1: equalibrium "eqb1" data read related, default to 1
s=1.0 : modifies the equilibrium while keeps the GS equation invariant.
The magnetic field can be written as
| Δ* ψ = J · ∇ φ = (p' + |
|
|
) |