


Next: Iterative Procedure for Determining
Up: Quasi-linear Tearing Mode Equations
Previous: Width of a Magnetic
Effect of Magnetic Islands on the Plasma Profiles
Suppose the pressure profile across the widest part of the island,
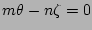 , is a uniform constant
, is a uniform constant 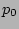 within the
island and is linear in the radius with slope
within the
island and is linear in the radius with slope
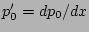 ,
just outside the shoulder of the island,
,
just outside the shoulder of the island,
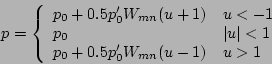 |
(29) |
where
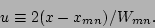 |
(30) |
Since
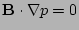 , the pressure is a function of
, the pressure is a function of
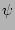 . At the widest part of the island, Eqs. (27),
(28), and (30) can be used to write
. At the widest part of the island, Eqs. (27),
(28), and (30) can be used to write 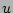 as a
function of
as a
function of 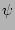
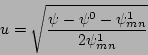 |
(31) |
Then, Eq. (29) can be used to express the pressure as a function
of 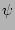 in the neighborhood of a magnetic island
in the neighborhood of a magnetic island
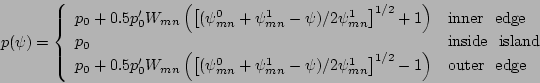 |
(32) |
Consider the poloidal (or, equivalently, the toroidal) average of
the pressure
at fixed 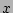 to determine the background axisymmetric pressure
profile to be used in Eq. (10). Substitution of
Eq. (27) in Eq. (32) and integration over
the poloidal angle leads to the following approximation to the
axisymmetric poloidal averaged pressure profile in the
neighborhood of a magnetic island
to determine the background axisymmetric pressure
profile to be used in Eq. (10). Substitution of
Eq. (27) in Eq. (32) and integration over
the poloidal angle leads to the following approximation to the
axisymmetric poloidal averaged pressure profile in the
neighborhood of a magnetic island
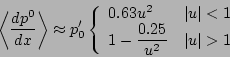 |
(33) |
It can be seen from Eq. (33) that the presence of a
magnetic island has the effect of flattening the axisymmetric
background pressure profile at the corresponding mode rational
surface. In particular,
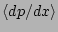 and
and
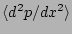 are both equal to zero at the mode
rational surface,
are both equal to zero at the mode
rational surface, 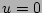 .
.
The same derivation can be applied to compute the flat spot in the
current density profile caused by the magnetic island at each mode
rational surface. Suppose the current density profile across the
widest part of the island is
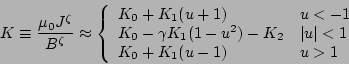 |
(34) |
with
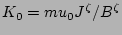 at the edge of the
island,
at the edge of the
island,
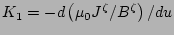 , at the
edge of the island. The coefficient,
, at the
edge of the island. The coefficient, 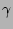 , is a current
peaking factor (if
, is a current
peaking factor (if 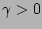 , assuming
, assuming 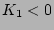 ) or current
suppression factor (if
) or current
suppression factor (if 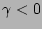 ) within the island, and
) within the island, and
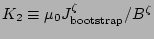 is the
bootstrap current density just outside the edge of the island.
Finally,
is the
bootstrap current density just outside the edge of the island.
Finally,
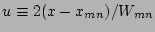 . Since the pressure
profile is assumed to be flat within the magnetic island, and the
bootstrap current density is roughly proportional to the pressure
gradient [11], there is no bootstrap current density
within the island. Hence, the abrupt transition from the presence
of bootstrap current outside of the island to the complete absence
of the bootstrap current within the island produces a square wave
contribution to the current suppression within the island. Close
to the mode rational surface, where
. Since the pressure
profile is assumed to be flat within the magnetic island, and the
bootstrap current density is roughly proportional to the pressure
gradient [11], there is no bootstrap current density
within the island. Hence, the abrupt transition from the presence
of bootstrap current outside of the island to the complete absence
of the bootstrap current within the island produces a square wave
contribution to the current suppression within the island. Close
to the mode rational surface, where 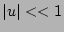 , the axisymmetric
average of the radial derivative of the toroidal current density
can be approximated with the following expression
, the axisymmetric
average of the radial derivative of the toroidal current density
can be approximated with the following expression
![\begin{displaymath}
\left\langle\frac{d}{dx}
\left(\frac{\mu_{0}J^{0\zeta}}{B^{0...
...sqrt{u^{2}+0.5}}\left[ 1 + \frac{3}{32(u^{2}+0.5)^{2}} \right]
\end{displaymath}](img105.png) |
(35) |
Thus, near the mode rational surface, the apparently singular
terms on the right side of equations (8) and
(10) reduce to the following non-singular forms
Consequently the Eqs. (8) and (10) are not
singular, and they can be integrated from the magnetic axis to the
edge of the plasma with a numerical ordinary differential equation
solver.
It should be noted that the interaction between different harmonics
can produce stochastic regions in the magnetic field near the X-points
of magnetic islands.
The effect of the stochastic regions will be to flatten the profiles
more completely near the mode rational surface than is estimated here.
In addition, multiple Fourier harmonics with the same ratio of
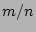 will produce magnetic islands with a cross-sectional
shape that is different from the single harmonic given in
Eq. (27).
The distortion in the island shape will also modify the estimates
given above for the profile flattening.
will produce magnetic islands with a cross-sectional
shape that is different from the single harmonic given in
Eq. (27).
The distortion in the island shape will also modify the estimates
given above for the profile flattening.



Next: Iterative Procedure for Determining
Up: Quasi-linear Tearing Mode Equations
Previous: Width of a Magnetic
transp_support
2008-12-08
![]() , is a uniform constant
, is a uniform constant ![]() within the
island and is linear in the radius with slope
within the
island and is linear in the radius with slope
![]() ,
just outside the shoulder of the island,
,
just outside the shoulder of the island,
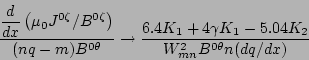
![]() will produce magnetic islands with a cross-sectional
shape that is different from the single harmonic given in
Eq. (27).
The distortion in the island shape will also modify the estimates
given above for the profile flattening.
will produce magnetic islands with a cross-sectional
shape that is different from the single harmonic given in
Eq. (27).
The distortion in the island shape will also modify the estimates
given above for the profile flattening.