


Next: gyro-Bohm term
Up: The Mixed Bohm/gyro-Bohm model
Previous: The Mixed Bohm/gyro-Bohm model
The mixed model is derived using the dimensional analysis approach,
whereby the diffusivity in a Tokamak plasma can be written as:
where 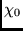 is some basic transport coefficient and F is a function
of the plasma dimensionless parameters
is some basic transport coefficient and F is a function
of the plasma dimensionless parameters
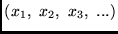 . We choose
for
. We choose
for 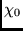 the Bohm diffusivity:
the Bohm diffusivity:
The expression of the dimensionless function F is chosen according to
the following criteria:
- The diffusivity must be bowl-shaped, increasing towards the plasma
boundary
- The functional dependencies of F must be in agreement with
scaling relationships of the global confinement time, reflecting
trends such as power degradation and linear dependence on plasma
current
- The diffusivity must provide the right degree of resilience
of the temperature profile
It easily shown that a very simple expression of F that satisfies
the above requirements is:
where q is the safety factor and
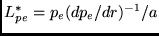 , being a the
plasma minor radius. The resulting expression of the diffusivity
can be written as:
, being a the
plasma minor radius. The resulting expression of the diffusivity
can be written as:
where 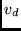 is the plasma diamagnetic velocity,
is the plasma diamagnetic velocity,  and
and 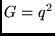 ,
so that it is clear that this model represents transport due to
long-wavelength turbulence.
,
so that it is clear that this model represents transport due to
long-wavelength turbulence.
The evidence coming up from the simulation of non-stationary
JET experiments [4](such as ELMs, cold pulses, sawteeth, etc.)
suggested that the above Bohm term should depend non-locally
on the plasma edge conditions through the temperature
gradient averaged over a region near the edge:
where x is the normalized toroidal flux coordinate. The final
expression of the Bohm-like model is:
where
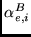 is a parameter to be determined empirically,
both for ions and electrons.
is a parameter to be determined empirically,
both for ions and electrons.



Next: gyro-Bohm term
Up: The Mixed Bohm/gyro-Bohm model
Previous: The Mixed Bohm/gyro-Bohm model
transp_support
2003-10-09
![]() , being a the
plasma minor radius. The resulting expression of the diffusivity
can be written as:
, being a the
plasma minor radius. The resulting expression of the diffusivity
can be written as: