Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

EM J03 2

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/EM J03 2]])

Jump to: navigation, search

Notes:

This problem was fairly easy. Our dear professor really likes the image charge problems. So do I.

Does anybody know where I can get the images for these problems? Maybe I shouldn't bother posting the problem statement.

The sizes are also screwed up. Love to fix that...

Problem Text:

2. This problem contains three questions on electrostatics.

a) A charge $Q$ is at $x = b$ and a second charge 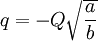$q = -Q\sqrt{\frac{a}{b}}$ is at $x = a$ . Show that the equipotential surface corresponding to $V = 0$ is described by a sphere with its center at the origin. Determine the radius $R$ of this sphere.

b) Find the electric potential in cylindrical coordinates $φ(r,θ, z)$ when a charge q is located at ( $r 0, z 0 > 0$ ) and there is a grounded conducting plane at $z = 0$ that has a conducting hemispherical bozz of radius Failed to parse (syntax error): R < b = \sqrt{r_0^2 + z_0^2}

whose center is at the origin. A side view of the boss and conducting plane is shown in the picture below.

(picture to be added)

c) What is the electrostatic force on the charge $q$ in Part b) for the case that $r 0 = 0$

Solution:

a) Potential relative to infinity: Failed to parse (syntax error): V(\vec{r}) = \frac{Q}{|\vec{r} - <b,0,0>|} - \frac{Q\sqrt{\frac{a}{b}}}{|\vec{r} - <a,0,0>|}

If 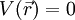$V(\vec{r}) = 0$ :

Failed to parse (syntax error): \frac{Q}{|\vec{r} - <b,0,0>|} = \frac{Q\sqrt{\frac{a}{b}}}{|\vec{r} - <a,0,0>|}

Failed to parse (syntax error): Q |\vec{r} - <a,0,0>| = Q\sqrt{\frac{a}{b}} |\vec{r} - <b,0,0>|

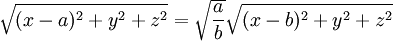
$\sqrt{(x - a)^2 + y^2 + z^2} = \sqrt{\frac{a}{b}} \sqrt{(x - b)^2 + y^2 + z^2}$

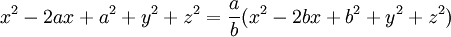
$x^2 - 2ax + a^2 + y^2 + z^2 = \frac{a}{b} (x^2 - 2bx + b^2 + y^2 + z^2)$

$(b - a)(x 2 + y 2 + z 2) + 2 x (a b - b a) = a b 2 - b a 2$

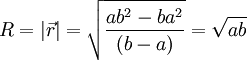
$R = |\vec{r}| = \sqrt{\frac{ab^2 - ba^2}{(b - a)}} = \sqrt{ab}$

b) The key to solving this part is realising that, since electrostatics is linear, and Laplace's equation is uniquely defined by a boundary, we can simply set the potential of the parts of the boundary which we are interested in to zero by creating the correct image charges.

How do we make the 'Boss' have $V = 0$ ? The obvious solution is to add a charge 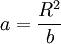$a = \frac{R^2}{b}$ to get $V (R) = 0$ .

What about the plane? Simply add the ordinary plane mirror image charges for both the $q$ and $Q$ charge.

There are then four effective point charges in the system. Let Failed to parse (syntax error): \vec{b}=<r_0,\theta_0,z_0>, \vec{b}_-=<r_0,\theta_0,-z_0>

- $q$ , at $\vec{b}$ .
$\vec{a}= \frac{R^2}{b^2}\vec{b}$ .
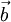$- q$ , at $\vec{b}_-$ .
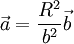$\vec{a}_-=\frac{R^2}{b^2}\vec{b}_-$ .

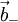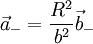Then, for Failed to parse (syntax error): r > R, z > 0, V(\vec{r}) = q\left[\frac{1}{|\vec{r} - \vec{b}|} - \frac{1}{|\vec{r} - \vec{b}_-|}\right] + Q\left[\frac{1}{|\vec{r} - \vec{a}|} - \frac{1}{|\vec{r} - \vec{a}_-|}\right]

c) Computer the electric field from the three image charges:

$E(\vec{r}) = -q\left[\frac{1}{|\vec{r} - \vec{b}|^2} - \frac{1}{|\vec{r} - \vec{b}_-|^2}\right] - Q\left[\frac{1}{|\vec{r} - \vec{a}|^2} - \frac{1}{|\vec{r} - \vec{a}_-|^2}\right]$