EM M01 2

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/EM M01 2]])
Jump to: navigation, search

First Solution

PlasmaWiki_Prelims_EM_M01_2.pdf (help ยท info)

Second Solution

In this problem, we investigate the effect of electromagnetic waves traveling through a gas of charged particles. This can happen when there is radio emission from a pulsar, and these signals propagate through clouds of charged particles in deep space before being detected on Earth. A linearly polarized radio wave will induce a charged current in the cloud which is proportional to the time-dependent electric field of the plane wave (ignore the motion of the charged particles due to the magnetic field of the plane wave).

a. Show that the dispersion relation between the frequency ω and the wavevector k for plane waves traveling through an electron gas can be written in terms of

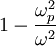
1-\frac{\omega_{p}^{2}}{\omega^{2}}

where ωp is the plasma frequency. Express the plasma frequency in terms of: 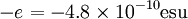-e=-4.8\times10^{-10}\mathrm{esu} (the electron charge) and ne (the volume density of electrons in the cloud).

b. For radio wave frequencies above ωp, how significant is the dispersion from ions (protons) in comparison to electrons?

c. Evaluate the phase velocity ω / k and the group velocity d\omega/dk and compare them to the speed of light. Write the phase and group velocities in terms of the ratio ω / ωp.

The Vela pulsar is about 500 parsecs distant (1 parsec= 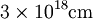3\times10^{18}\mathrm{cm} ). It emits radio waves over a broad band. When observations are made in narrow frequency bands, what is observed are narrow pulses which arrive at a fixed period, similar to a timing signal for synchronizing a clock.

d. The narrow pulses observed at 1660 MHz are delayed relative to the narrow pulses observed at 1720 MHz by 6.8 ms. If this is interpreted by the dispersion in an ionized gas, what is the mean density of free electrons between Vela and us? To simplify the calculation, you can anticipate that 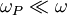\omega_{P}\ll\omega.

We start off with some of Maxwell's equations:

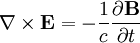
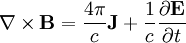
\nabla\times\mathbf{E}=-\frac{1}{c}\frac{\partial\mathbf{B}}{\partial t} \nabla\times\mathbf{B}=\frac{4\pi}{c}\mathbf{J}+\frac{1}{c}\frac{\partial\mathbf{E}}{\partial t}

And the vector relation:

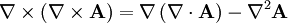
\nabla\times\left(\nabla\times\mathbf{A}\right)=\nabla\left(\nabla\cdot\mathbf{A}\right)-\nabla^{2}\mathbf{A}

Taking the cross product of the first relation and using the vector identity:

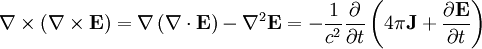
\nabla\times\left(\nabla\times\mathbf{E}\right)=\nabla\left(\nabla\cdot\mathbf{E}\right)-\nabla^{2}\mathbf{E}=-\frac{1}{c^2}\frac{\partial}{\partial t}\left(4\pi \mathbf{J}+\frac{\partial\mathbf{E}}{\partial t}\right)

We can rewrite the current as:

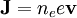
\mathbf{J}=n_{e}e\mathbf{v}

And writing the Lorentz force equation

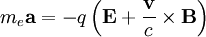
m_{e}\mathbf{a}=-q\left(\mathbf{E}+\frac{\mathbf{v}}{c}\times\mathbf{B}\right)

Since v1 is a perturbed quantitiy and v0 = 0, we can assume it is small compared to c and neglect the magnetic contribution to the lorentz force:

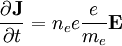
\frac{\partial\mathbf{J}}{\partial t}=n_{e}e\frac{e}{m_{e}}\mathbf{E}

so that:

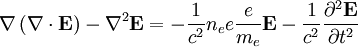
\nabla\left(\nabla\cdot\mathbf{E}\right)-\nabla^{2}\mathbf{E}=-\frac{1}{c^2}n_{e}e\frac{e}{m_{e}}\mathbf{E}-\frac{1}{c^2}\frac{\partial^{2}\mathbf{E}}{\partial t^{2}}

We can write the perturbed values in terms of plane waves moving in the 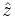\hat{z} direction, for example:

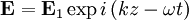
\mathbf{E}=\mathbf{E}_{1}\exp i\left(kz-\omega t\right)

Here we have taken E0 = 0 (no zero order electric field). Plugging in:

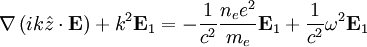
\nabla\left(ik\hat{z}\cdot\mathbf{E}\right)+k^{2}\mathbf{E}_{1}=-\frac{1}{c^2}\frac{n_{e}e^{2}}{m_{e}}\mathbf{E}_{1}+\frac{1}{c^2}\omega^{2}\mathbf{E}_{1}

The first term on the left must be zero, since the electric field must be perpendicular to the wave vector:

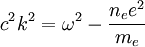
c^2 k^2=\omega^{2}-\frac{n_{e}e^{2}}{m_{e}}

Defining 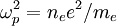\omega_{p}^{2}=n_{e}e^{2}/m_{e}, we get the dispersion relation:

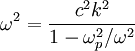
\omega^{2}=\frac{c^2 k^{2}}{1-\omega_{p}^{2}/\omega^{2}}

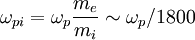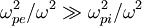For frequencies above ωp, dispersion from ions have negligible dispersion compared to electrons, since the response from ions will be like \omega_{pi}=\omega_{p}\frac{m_{e}}{m_{i}}\sim\omega_{p}/1800 because of the mass in the frequency. This means that \omega_{pe}^{2}/\omega^{2}\gg\omega_{pi}^{2}/\omega^{2}.

The phase velocity is just:

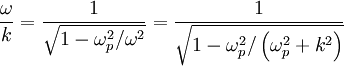
\frac{\omega}{k}=\frac{1}{\sqrt{1-\omega_{p}^{2}/\omega^{2}}}=\frac{1}{\sqrt{1-\omega_{p}^{2}/\left(\omega_{p}^{2}+k^{2}\right)}}

where for the second equality we use the dispersion relation again. The group velocity can be found by differentiating:

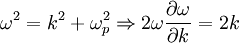
\omega^{2}=k^{2}+\omega_{p}^{2}\Rightarrow2\omega\frac{\partial\omega}{\partial k}=2k

Moving around and substituting in the phase velocity:

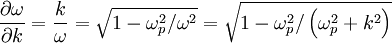
\frac{\partial\omega}{\partial k}=\frac{k}{\omega}=\sqrt{1-\omega_{p}^{2}/\omega^{2}}=\sqrt{1-\omega_{p}^{2}/\left(\omega_{p}^{2}+k^{2}\right)}

From part c:

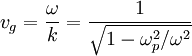
v_{g}=\frac{\omega}{k}=\frac{1}{\sqrt{1-\omega_{p}^{2}/\omega^{2}}}

The time it takes a pulse of frequency ω to cross to here:

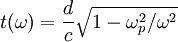
t(\omega)=\frac{d}{c}\sqrt{1-\omega_{p}^{2}/\omega^{2}}

Simplifying using 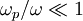\omega_{p}/\omega\ll1:

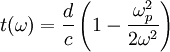
t(\omega)=\frac{d}{c}\left(1-\frac{\omega_{p}^{2}}{2\omega^{2}}\right)

So that the difference in time is given by:

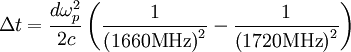
\Delta t=\frac{d\omega_{p}^{2}}{2c}\left(\frac{1}{\left(1660\mathrm{MHz}\right)^{2}}-\frac{1}{\left(1720\mathrm{MHz}\right)^{2}}\right)

Plugging in for everything:

\begin{matrix} 6.8\times10^{-3}\mathrm{s} &amp; = &amp; \frac{\left(500\times3\times10^{18}\mathrm{cm}\right)n_{e}\left(4.8\times10^{-10}\mathrm{esu}\right)^{2}}{2\left(3\times10^{10}\mathrm{cm/s}\right)\left(9.1\times10^{-28}\mathrm{g}\right)} \\ &amp;&amp;\cdot\left(\frac{1}{\left(1.66\times10^{9}\mathrm{s}^{-1}\right)^{2}}-\frac{1}{\left(1.72\times10^{9}\mathrm{s}^{-1}\right)^{2}}\right) \end{matrix}

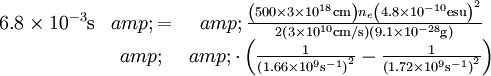
and solving:

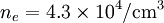
n_{e}=4.3\times10^{4}\mathrm{/cm^{3}}

This page was recovered in October 2009 from the Plasmagicians page on Prelim_M01_EM2 dated 19:23, 6 June 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/EM_M01_2"
Personal tools