SM J04 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/SM J04 1]])
Jump to: navigation, search

First Solution

PlasmaWiki_Prelims_SM_J04_1.pdf (help ยท info)


Second Solution

Consider N non-interacting quantized spins in a magnetic field 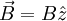\vec{B}=B\hat{z}. The energy of the spins is − BMz, where:

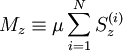
M_{z}\equiv\mu\sum_{i=1}^{N}S_{z}^{(i)}

is the total magnetization. For each spin, 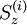S_{z}^{(i)} takes only 2S+1 values -S, -S+1, ..., S-1, S. Given the temperature of the system T:

a. Calculate the Gibbs partition function Z(T,B);

b. Calculate the Gibbs free energy G(T,B) and evaluate its asymptotic behavior at weak ( 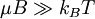\mu B\gg k_{B}T ) magnetic field;

c. Calculate the zero-field magnetic susceptibility

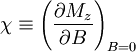
\chi\equiv\left(\frac{\partial M_{z}}{\partial B}\right)_{B=0}

d. Calculate the magnetic susceptibility at strong fields 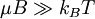\mu B\gg k_{B}T .

The partition function for one particle is given by:

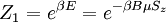
Z_{1}=e^{\beta E}=e^{-\beta B\mu S_{z}}

We can get the expectation of Sz by:

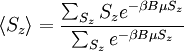
\langle S_{z}\rangle=\frac{\sum_{S_{z}}S_{z}e^{-\beta B\mu S_{z}}}{\sum_{S_{z}}e^{-\beta B\mu S_{z}}}

Where the sums are over all possible values of Sz. Using this, we get the total partition function to be:

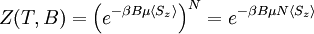
Z(T,B)=\left(e^{-\beta B\mu\langle S_{z}\rangle}\right)^{N}=e^{-\beta B\mu N\langle S_{z}\rangle}

The Gibbs free energy may be found by:

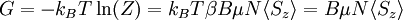
G=-k_{B}T\ln(Z)=k_{B}T\beta B\mu N\langle S_{z}\rangle=B\mu N\langle S_{z}\rangle

In the case that 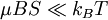\mu BS\ll k_{B}T , eβμBS˜1, and so we find:

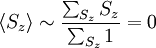
\langle S_{z}\rangle\sim\frac{\sum_{S_{z}}S_{z}}{\sum_{S_{z}}1}=0

so that the Gibbs free energy 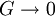G\rightarrow0.

In the other case that 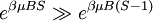e^{\beta\mu BS}\gg e^{\beta\mu B(S-1)}, so:

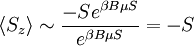
\langle S_{z}\rangle\sim\frac{-Se^{\beta B\mu S}}{e^{\beta B\mu S}}=-S

and the Gibbs free energy 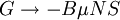G\rightarrow-B\mu NS.

The magnetic susceptibility is defined by:

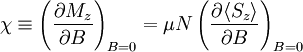
\chi\equiv\left(\frac{\partial M_{z}}{\partial B}\right)_{B=0}=\mu N\left(\frac{\partial\langle S_{z}\rangle}{\partial B}\right)_{B=0}

Taking the derivative

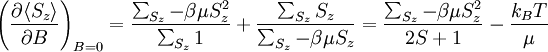
\left(\frac{\partial\langle S_{z}\rangle}{\partial B}\right)_{B=0}=\frac{\sum_{S_{z}}-\beta\mu S_{z}^{2}}{\sum_{S_{z}}1}+\frac{\sum_{S_{z}}S_{z}}{\sum_{S_{z}}-\beta\mu S_{z}}=\frac{\sum_{S_{z}}-\beta\mu S_{z}^{2}}{2S+1}-\frac{k_{B}T}{\mu}

Plugging in:

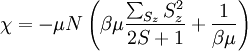
\chi=-\mu N\left(\beta\mu\frac{\sum_{S_{z}}S_{z}^{2}}{2S+1}+\frac{1}{\beta\mu}\right)

1.1.4 Part d

This is similar to the last part, but we get:

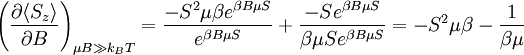
\left(\frac{\partial\langle S_{z}\rangle}{\partial B}\right)_{\mu B\gg k_{B}T}=\frac{-S^{2}\mu\beta e^{\beta B\mu S}}{e^{\beta B\mu S}}+\frac{-Se^{\beta B\mu S}}{\beta\mu Se^{\beta B\mu S}}=-S^{2}\mu\beta-\frac{1}{\beta\mu}

So that:

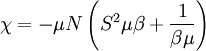
\chi=-\mu N\left(S^{2}\mu\beta+\frac{1}{\beta\mu}\right)

This page was recovered in October 2009 from the Plasmagicians page on Prelim_J04_SMT1 dated 02:24, 13 August 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/SM_J04_1"
Personal tools