GPU Programming at PPPL

Written by Eliot Feibush & Michael Knyszek

Introduction

Programming on Graphical Processing Units (GPUs) is incredibly powerful in that it takes advantage of parallelism on a scale much larger than most of today's supercomputers. Rather than relying on massive amounts of machines which communicate with high-latency connections, GPUs have a massive amount of tightly-knit, incredibly lean cores that are heavily optimized for floating point operations. What this means is that you can have millions of points on a grid processed potentially hundreds of times faster than if you processed them serially. A fuller, broader introduction to the power of GPUs can be found in the following NVIDIA presentation for their new Tesla GPUs:

Tesla GPU Computing: Accelerating High Performance Computing

Although GPUs are fairly specialized in their computation, NVIDIA has conveniently provided a list of just some of the many applications of hardware accelerated computing ranging from finance to science and research:
Popular GPU Accelerated Applications

Table of Contents


GPU Devices at PPPL

cppg-6 Linux computer

An NVIDIA Tesla K20c GPU accelerator is installed in cppg-6.  The computer's original 525 watt power supply was replaced with a 1000 watt power supply to power the 233 watt board.  The K20c receives 80 watts from the PCI bus and 2 six pin power cables deliver the rest of the power.  There are 2496 CUDA cores in this GPU.  It contains 5 GB of on-board memory.

The computer is a Dell Precision T3500n with a 64-bit Intel Quad Core Xeon processor.  It contains 4 GB of host memory.  The graphics board is an NVIDIA Quadro FX 580 that drives 2 monitors at 1600 x 1200 resolution each.  The graphics board is also a CUDA device with 32 cores. This computer mounts the PPPL file system when you log in.

Note:  it is currently running 64-bit Red Hat 5 kernel. This computer mounts the PPL cluster file system so you can load PPL modules as on portal.

ssh into cppg-6 to run the GPU software.

gpusrv GPU Cluster

gpusrv01

Two NVIDIA M2070 GPU accelerators are installed on gpusrv01.   These GPUs have 443 CUDA cores each and 5 GB of on-board memory.

gpusrv02

Two NVIDIA Tesla K20m GPU accelerators are installed in gpusrv02.  There are 2496 CUDA cores in each GPU and each GPU contains 4.8 GB of on-board memory.

Run the "useg" or "use" command to be queued for access onto gpusrv.

Back to Top ➚


NVIDIA software

The NVIDIA SDK CUDA 5.0.35 (64-bit) software is installed in /usr/pppl/cuda/cudatoolkit/5.0.35.  The package includes nvcc for cross compiling cuda programs to run on the K20.

At the Linux command line: module load cuda/5.0.35

/usr/bin/nvidia-smi -q
    This program prints information about the NVIDIA devices installed in the computer.  There is a man page for nvidia-smi or you can run nvidia-smi -h  to see a list of command line options.

Another sample program is in /p/vis/cuda/samples/devicequerydrv.  The deviceQueryDrv program there prints information about the installed NVIDIA devices. The following output is an example of running deviceQueryDrv on cppg-6:

CUDA Device Query (Driver API) statically linked version
Detected 2 CUDA Capable device(s)

Device 0: "Tesla K20c"
  CUDA Driver Version:                           5.0
  CUDA Capability Major/Minor version number:    3.5
  Total amount of global memory:                 4096 MBytes (4294967295 bytes)
  (13) Multiprocessors x (192) CUDA Cores/MP:    2496 CUDA Cores
  GPU Clock rate:                                706 MHz (0.71 GHz)
  Memory Clock rate:                             2600 Mhz
  Memory Bus Width:                              320-bit
  L2 Cache Size:                                 1310720 bytes
  Max Texture Dimension Sizes                    1D=(65536) 2D=(65536,65536) 3D=(4096,4096,4096)
  Max Layered Texture Size (dim) x layers        1D=(16384) x 2048, 2D=(16384,16384) x 2048
  Total amount of constant memory:               65536 bytes
  Total amount of shared memory per block:       49152 bytes
  Total number of registers available per block: 65536
  Warp size:                                     32
  Maximum number of threads per multiprocessor:  2048
  Maximum number of threads per block:           1024
  Maximum sizes of each dimension of a block:    1024 x 1024 x 64
  Maximum sizes of each dimension of a grid:     2147483647 x 65535 x 65535
  Texture alignment:                             512 bytes
  Maximum memory pitch:                          2147483647 bytes
  Concurrent copy and kernel execution:          Yes with 2 copy engine(s)
  Run time limit on kernels:                     No
  Integrated GPU sharing Host Memory:            No
  Support host page-locked memory mapping:       Yes
  Concurrent kernel execution:                   Yes
  Alignment requirement for Surfaces:            Yes
  Device has ECC support:                        Enabled
  Device supports Unified Addressing (UVA):      No
  Device PCI Bus ID / PCI location ID:           3 / 0
  Compute Mode:
     < Default (multiple host threads can use ::cudaSetDevice() with device simultaneously) >

Device 1: "Quadro FX 580"
  CUDA Driver Version:                           5.0
  CUDA Capability Major/Minor version number:    1.1
  Total amount of global memory:                 511 MBytes (536150016 bytes)
  ( 4) Multiprocessors x (  8) CUDA Cores/MP:    32 CUDA Cores
  GPU Clock rate:                                1125 MHz (1.12 GHz)
  Memory Clock rate:                             800 Mhz
  Memory Bus Width:                              128-bit
  Max Texture Dimension Sizes                    1D=(8192) 2D=(65536,32768) 3D=(2048,2048,2048)
  Max Layered Texture Size (dim) x layers        1D=(8192) x 512, 2D=(8192,8192) x 512
  Total amount of constant memory:               65536 bytes
  Total amount of shared memory per block:       16384 bytes
  Total number of registers available per block: 8192
  Warp size:                                     32
  Maximum number of threads per multiprocessor:  768
  Maximum number of threads per block:           512
  Maximum sizes of each dimension of a block:    512 x 512 x 64
  Maximum sizes of each dimension of a grid:     65535 x 65535 x 1
  Texture alignment:                             256 bytes
  Maximum memory pitch:                          2147483647 bytes
  Concurrent copy and kernel execution:          Yes with 1 copy engine(s)
  Run time limit on kernels:                     Yes
  Integrated GPU sharing Host Memory:            No
  Support host page-locked memory mapping:       Yes
  Concurrent kernel execution:                   No
  Alignment requirement for Surfaces:            Yes
  Device has ECC support:                        Disabled
  Device supports Unified Addressing (UVA):      No
  Device PCI Bus ID / PCI location ID:           2 / 0
  Compute Mode:
     < Default (multiple host threads can use ::cudaSetDevice() with device simultaneously) >

It identifies the K20 as the first device.  This is convenient for the CUDA examples that appear later on in this document.

For more information about the GPU driver and NVIDIA software included with the CUDA Toolkit, click on the course link below:
GPU driver/CUDA

Back to Top ➚


Basic GPU Programming

Programming Course

More information on all three sections below can be found in a larger course presentation which is very long, but contains information on all 3 types of CUDA programming.

Click the link below to look at the full 107 slide course:
Full 3-part Introduction

Introduction to CUDA Libraries

In most cases, utilizing libraries built for performing various mathematical operations and transformations may just be the easiest way to take advantage of GPU parallelism.
CUDA Libraries such as: can make paralleling codes for the GPU trivial by simply "dropping in" library calls where you would otherwise perform certain mathematical operations.

For a more detailed overview and some tips on how to get started with the CUDA libraries, click on the course link below:
NVIDIA CUDA Library Approach (First ~30 Pages of the Large Course Above)

For more information about the Thrust library specifically, check out:
An Introduction to the Thrust Parallel Algorithms Library

Introduction to OpenACC

For anyone familiar with OpenMP, working with OpenACC should be very easy.
OpenACC is built on similar principles to OpenMP in that parallelism is as simple as adding directives to your C/Fortran codes.

For a more detailed overview and some tips on how to get started with OpenACC, click on the course link below:
GPU Computing with OpenACC Directives

Introduction to CUDA C/C++

CUDA C/C++ is the most involved and most powerful form of GPU programming of the above methods.
Built as an extension to C/C++, the language is easy to get started with but the runtime can be tricky to master. However, it is extremely powerful and offers the greatest degree of customization and is the biggest opportunity for a speed boost in your code.

For a more detailed overview and some tips on how to get started with CUDA C/C++, click on the course link below:
CUDA C/C++ Basics

Below is also a cheatsheet with some of the basic functions, syntax, and ideas of CUDA C/C++:
CUDA C/C++ Cheatsheet

Back to Top ➚

Simple CUDA Examples

The NVIDIA training course provided several programming examples. 
Loading the cuda module should set up your include path and library path for compiling and linking the example programs.
There are some sample CUDA programs in /p/vis/cuda/samples/test. 
The source code is in these files:
The Makefile will compile and link the codes so you can run the examples:
Back to Top ➚


More Sophisticated CUDA Examples

Generating Fractals

GPUs excel at performing many simultaneous computations that are mutually independent. Perhaps one of the best examples of this is in generating images of fractals since each point is calculated independently, sharing only the same base equation. Two particularly interesting fractals are those in the Mandelbrot set and the Julia set, which are defined by the equation



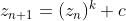
where z and c are complex numbers. Here is an example of what the code below should produce:



(The short tutorial below does not run through coloring methods, but to achieve the same coloring effect, take a rainbow palette and use the output of the program to interpolate between colors on a log2 scaling.)

To generate images of these fractals, we iteratively compute the equation at discrete points and count the iterations it takes for the absolute value of z to exceed a certain threshold. This is a measure of how quickly the equation diverges and is interesting because it produces fractal patterns. From this measure, we can then color and draw the fractal. This is the simplest way to generate fractals and is known as the Escape Time Algorithm, since it measure how quickly the recursive equation "escapes" a certain bailout radius (the threshold). If you are more interested in learning about the math behind it, Wikipedia actually has an excellent amount of information on the subject. This example will instead focus on the GPU implementation aspect.

In this particular example, we need to define a few things. First of all, we represent our image as simple an array of floating point numbers in memory. Next, we need a way to pass the dimensions of the image and what our "viewing window" is (the maximum and minimum coordinates in the Argand plane to view). The solution to passing all these arguments will be to use a special part of the GPU called constant memory. It consists of a small amount of read-only memory set aside for constants which are going to be accessed frequently over all threads running in a kernel. We do this by first defining a C struct with all our information, like so: 
typedef struct {
    int width;
    int height;
    float x_max;
    float x_min;
    float y_max;
    float y_min;
    float c_re;
    float c_im;
} Dimensions;
Now we want to place an instance of our struct onto the GPU for access. First, we need to declare some space in constant memory: 
__constant__ Dimensions dev_d;
Second, we have to create our own instance, and then simply copy it over! Supposing the variable "d" is a pointer to our host-side Dimensions instance, we simply run the following code: 
cudaMemcpyToSymbol(dev_d, d, sizeof(Dimensions), 0, cudaMemcpyHostToDevice);
One thing to keep in mind about constant memory is that for a warp of threads (all the threads sharing a block) there is a 32-bit cache for constant memory which can make reads of constant memory extremely fast. The limitation here is that the cache size is absolutely tiny. For a few constants, however, this can really improve performance over reading the constant from global memory. One should use constant memory with extreme care since, if used improperly, could lead to a serious bottleneck in computation. A few constants is okay, but having an array of hundreds of values would destroy the purpose of constant memory.
An example of device code for a GPU implementation of a Mandelbrot set fractal generator would look something like the following. Note: we assume our equation here has k=2 which makes exponentiating the complex number simple with just floats. 
__global__ void mandelbrot(float *img) {

    // Get the current index based on thread and block number
    int index = threadIdx.x + blockIdx.x * blockDim.x; 
    
    // Derive x and y points
    int Px = index % dev_d.width;
    int Py = index / dev_d.width;
    
    // Scale x-y coordinates into predefined scaling options
    // x0 and y0 are part of our constant c, in the mandelbrot case
    float x0 = (float)Px*(dev_d.x_max - dev_d.x_min)/((float)dev_d.width) + (float)dev_d.x_min;
    float y0 = (float)Py*(dev_d.y_max - dev_d.y_min)/((float)dev_d.height) + (float)dev_d.y_min;
    
    // Set some other variables, x and y are parts of a complex number, z0 = x + yi
    float x = 0;
    float y = 0;
    float tmp;
    int i = 0;
    
    // Perform the escape-time iteration scheme
    // BAILOUT_RADIUS is our threshold, MAX_ITER is how many iterations to
    // perform before giving up and assuming the equation converges.
    while(x*x + y*y < BAILOUT_RADIUS && i < MAX_ITER) {
        // Square z (x + iy) and add c (x0 + iy0)
        tmp = x*x - y*y + x0;
        y = 2*x*y + y0;
        x = tmp;
        ++i;
    }
    
    // Part of the "Normalized Iteration Count Algorithm", converts an integer iteration count into
    // a real number. Not particularly important, but useful for making coloring smoother.
    if(i == MAX_ITER) img[index] = (float) i;
    else img[index] = (float) i + 1.5 - log2(log2(x*x+y*y)/2);
}
All that is left to do is to follow the steps of setting up our environment and running the kernel. If you have gone through the course above, the following methods for setting up our image on the GPU and copying it back should seem very familiar. 
float *d_pixels; // pointer to image on device
float *h_pixels; // pointer to image on host

// size is the number of pixels in the image
h_pixels = (float*) malloc(size * sizeof(float)); // Allocate memory on host
cudaMalloc((void **) &d_pixels, size * sizeof(float)); // Allocate memory on device

// Start kernel, size is assumed divisible by THREADS_PER_BLOCK
mandelbrot <<< size/THREADS_PER_BLOCK, THREADS_PER_BLOCK >>> (d_pixels);

// Copy our processed image onto the host
cudaMemcpy(h_pixels, d_pixels, size * sizeof(float), cudaMemcpyDeviceToHost);

// Force the host to wait for the device to finish so we do not write garbage data into the image
cudaDeviceSynchronize();

// ... Insert Image Writing Code Here ...
With this simple setup, you can implement a whole host of variations. For example, you could generate Julia set fractals, make fractal movies by altering parameters slightly, such as the constant for the Julia set or the exponent "k" which the equation uses.
All these features and more are implemented and can be examined by simply going into /u/mknyszek/cuda/fractals and having a look at the files.

Here are some videos of these features in action:

Back to Top ➚

2D Fluid Simulation

Another useful application of GPU programming is fluid simulations. In this particular example, we will be working with the Navier-Stokes Equations for incompressible, constant density fluids:





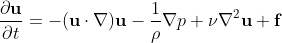
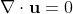
And this tutorial will introduce an "ink" whose density will not be constant and will be moved about by the fluid. The density of the "ink" can be described by the following equation:






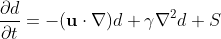
Like the previous fractals example, this tutorial will not dive too deeply into the mathematics. However, it is important to understand what numerical methods we are using here. The methods described here will be based upon the paper Stable Fluids (Stam, 1999) (ACM Entry) for some calculations, and we will simply take advantage of finite difference forms for other calculations. To summarize, the idea here is that we perform advection, diffusion, and the addition of body forces to a velocity with non-zero divergence. Afterwards, we calculate the pressure (which can be represented as a Poisson equation) at each point on the grid using a Jacobi solver, and subtract the gradient at each point from the our velocity to project it onto a space where it has a divergence of zero, satisfying the second equation above. We will also use the stable method for calculating advection as described in Stable Fluids, Stam, 1999, which involves moving backwards in time rather than forwards, which will be explained further down.

Some more important details about this implementation are: Our overall approach will look something like this:
  1. Add Body Forces to Velocity and Add "ink" from Sources
  2. Advect Velocity and Density ("ink")
  3. Calculate Divergence of Velocity
  4. Solve Pressure Poisson Equation using the Jacobi Method: Ax=b where x is pressure and b is velocity divergence.
  5. Use Pressure to Correct/Project Velocity to be Divergence-Free
  6. Write Density ("ink") Values to Image
First, we define our Dimensions struct and constant memory allocation: 
typedef struct {
    int width;
    int height;
    int steps;
    float timestep;    // Timestep in Seconds
    float dissipation; // Mass Dissipation Constant (how our "ink" dissipates over time). Set to 1 for no dissipation, 0.995 tends to look nice though.
} Dimensions;

...

__constant__ Dimensions ddim;
Next, we will define all our kernels and methods. By design, and unlike the fractals example, we will have many kernels that will be performing operations over a large number of points in parallel. Think of these operations as "slab" operations, performing calculations on large areas of memory simultaneously.
Organizing the code this way with many kernels keeps things organized with only minor overhead. Potentially, you could gain a speed boost by performing many of these operations in a single kernel, but you have to be careful to make sure you call __syncthreads() the proper amount of times. We use this multiple kernel technique for simplicity and clarity.

Add Forces/Sources

This is a very simple procedure. We simply add whatever our force or source amount is multiplied by the size of our timestep to each point in our grid.
__global__ void add_source(float *d, float *s) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int width = ddim.width;
    int height = ddim.height;
    int px = i % width;
    int py = i / width;
    
    // Skip Boundary values
    if(px > 0 && py > 0 && px < width-1 && py < height-1) 
    {
        // Add source each timestep
        d[i] += ddim.timestep * s[i];
    }
}
The first argument is left as just "d" because we will use this same kernel to add our body forces to the horizontal and vertical components of velocity, in addition to "ink" density.

Advection

The advection kernel is significantly more complicated. As described in Stable Fluids (Stam 1999), trying to advect density or velocity forward in time (by taking the previous velocity at each point and following it to a new point and putting that velocity there) is unstable and leads to oscillations in the calculation over time. Instead, here we take the velocity at each point, follow it in its opposite direction, and find the velocity at that point using bilinear interpolation. We then update the velocity at our current point with that interpolated velocity.
Conveniently, it turns out that the unstable method is also unsuitable for GPU programming because we can end up with multiple threads trying to write to the same memory location, which can cause serious problems! With this method, each thread safely updates only its own dedicated grid point while only reading other, old grid points. 
__global__ void advect(float *dold, float *d, float *u, float *v, float md) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int width = ddim.width;
    int height = ddim.height;
    int px = i % width;
    int py = i / width;
    
    int px0, py0, px1, py1;
    float x, y, dx0, dx1, dy0, dy1;
    
    // Skip Boundary values
    if(px != 0 && py != 0 && px != width-1 && py != height-1) 
    {
        // Move "backwards" in time
        x = px - ddim.timestep * (width-2)  * u[i]; // Multiply by the width of the grid not including the boundary
        y = py - ddim.timestep * (height-2) * v[i]; // Multiply by the height of the grid not including the boundary
        
        // Clamp to Edges, that is, if the velocity goes over the edge, clamp it to the boundary value
        if (x < 0.5) x = 0.5; if (x > width - 1.5)  x = width - 1.5;
        if (y < 0.5) y = 0.5; if (y > height - 1.5) y = height - 1.5;
        
        // Setup bilinear interpolation "corner points"
        px0 = (int) x; px1 = px0 + 1; dx1 = x - px0; dx0 = 1 - dx1;
        py0 = (int) y; py1 = py0 + 1; dy1 = y - py0; dy0 = 1 - dy1;
        
        // Perform a bilinear interpolation
        d[i] = dx0 * (dy0 * dold[px0 + width*py0] + dy1 * dold[px0 + width*py1]) +
               dx1 * (dy0 * dold[px1 + width*py0] + dy1 * dold[px1 + width*py1]);
               
        // Multiply by the mass dissipation constant
        d[i] *= md;
    }
    
    return;
}
Here again, "d" is a placeholder variable since we will use both velocities and density in its place. "dold" refers to the array of previous values and "d" refers to the array storing new values.

Divergence

For calculating the divergence, we use the finite difference method for the divergence of a vector field. In our case, delta x and delta y are both 1 (since we define the grid size to be one-to-one with pixels). Thus, our kernel is simply: 
__global__ void divergence(float *u, float *v, float *div) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int width = ddim.width;
    int height = ddim.height;
    int px = i % width;
    int py = i / width;
    
    // Skip Boundary values
    if(px > 0 && py > 0 && px < width-1 && py < height-1) 
    {
        float u_l = u[i-1];
        float u_r = u[i+1];
        float v_t = v[px + (py-1)*width];
        float v_b = v[px + (py+1)*width];
        
        // Calculate divergence using finite difference method
        // We multiply by -1 here to reduce the number of negative multiplications in the pressure calculation
        div[i] = -0.5 * ((u_r - u_l)/(width-2) + (v_b - v_t)/(height-2)); 
    }
}

Pressure

We implement here a kernel for one iteration of the Jacobi solver for pressure, which can be represented a Poisson equation. Since the step of each solver depends on the last, we have to perform some pointer manipulations and boundary updates in between iterations, which is why we implement it this way. 
__global__ void pressure(float *u, float *v, float *p, float *pold, float *div) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int width = ddim.width;
    int height = ddim.height;
    int px = i % width;
    int py = i / width;
    
    // Skip Boundary values
    if(px > 0 && py > 0 && px < width-1 && py < height-1) 
    {
        // left, right, top, bottom neighbors
        float x_l = p[i-1];
        float x_r = p[i+1];
        float x_t = p[px + (py-1)*width];
        float x_b = p[px + (py+1)*width];
        float b = div[i];
        
        // Jacobi method for solving the pressure Poisson equation
        pold[i] = (x_l + x_r + x_t + x_b + b) * 0.25; // Here b is positive because of the extra negative sign in the divergence calculation
    }
}
Normally the Jacobi method is one of the methods that converges the most slowly. However, on the GPU each Jacobi iteration is incredibly cheap since the entire pressure array is updated nearly simultaneously. It is possible to implement the red-black Gauss-Siedel relaxation algorithm to solve for pressure, however this is more unnecessarily complex for the sake of this tutorial. From a GPU programming perspective, each step is very similar and no real benefit is gained from that implementation. Regardless, for an interesting look into the method, see this publication from the Universidade da Beira Interior.

Projection/Correction

Nothing very interesting occurs in this kernel. Essentially, the finite difference method for taking the gradient of a scalar field is used (with dx and dy being 1) to get the gradient of pressure. Each component of the gradient is then subtracted from the respective velocity component. 
__global__ void correction(float *u, float *v, float *p) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int width = ddim.width;
    int height = ddim.height;
    int px = i % width;
    int py = i / width;
    
    // Skip Boundary values
    if(px > 0 && py > 0 && px < width-1 && py < height-1) {
    
        // left, right, top, bottom neighbors
        float p_l = p[i-1];
        float p_r = p[i+1];
        float p_t = p[px + (py-1)*width];
        float p_b = p[px + (py+1)*width];
        
        // Find the gradient and perform the correction/projection
        u[i] -= 0.5*(p_r - p_l)*(width-2);
        v[i] -= 0.5*(p_b - p_t)*(height-2);
    }
}

Boundary Conditions

In order to enforce our defined boundary conditions (no-slip and pure Neumann), we have to have kernels to occasionally update the boundary conditions of both velocity components and pressure.

For velocity, we want the edge between the boundary grid points and the closest inner grid point to have a horizontal velocity of zero for vertical edges, and a vertical velocity of zero for horizontal edges. Simply by looking at the finite difference method, we see we can do this by setting the boundary grid point velocities to be negative that of the velocity directly inside. 
__global__ void velocity_bc(float *u, float *v) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int width = ddim.width;
    int height = ddim.height;
    int px = i % width;
    int py = i / width;

    // Skip Inner Values
    if(px == 0) 
    {
        u[i] = -u[i+1];
        v[i] =  v[i+1];
    } 
    else if(py == 0) 
    {
        u[i] =  u[px + (py+1)*width];
        v[i] = -v[px + (py+1)*width];
    } 
    else if(px == width-1) 
    {
        u[i] = -u[i-1];
        v[i] =  v[i-1];
    } 
    else if(py == height-1) 
    {
        u[i] =  u[px + (py-1)*width];
        v[i] = -v[px + (py-1)*width];
    }
}
For pressure, we want the edge between the boundary grid points and the closest inner grid point to have a derivative of zero with respect to the normal. By using the finite difference method for the derivative of pressure in the direction of the normal, we see that our pressure on the boundary grid point needs to be set equal to the pressure value of the closest inner grid point. 
__global__ void pressure_bc(float *p) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    int width = ddim.width;
    int height = ddim.height;
    int px = i % width;
    int py = i / width;

    // Skip Inner Values
    if(px == 0) 
    {
        p[i] = p[i+1];
    } 
    else if(py == 0) 
    {
        p[i] = p[px + (py+1)*width];
    } 
    else if(px == width-1) 
    {
        p[i] = p[i-1];
    } 
    else if(py == height-1) 
    {
        p[i] = p[px + (py-1)*width];
    }
}

Putting It All Together

Finally, we just have to put this all together in the step order we described above (with a few extra pointer swaps, boundary value updates, and memory updates in between).
For reference, we set up all our variables first, like we did for the fractals example: 
// Full size of arrays, including boundaries
int size = dim->width * dim->height; 

// size is necessarily divisible by a constant THREADS_PER_BLOCK defined elsewhere
int blocks = size/THREADS_PER_BLOCK;

//
// All Device Pointers
//

//velocity and pressure
float *u, *v, *p;
float *uold, *vold, *pold;
float *utemp, *vtemp, *ptemp; // temp pointers, DO NOT INITIALIZE

//divergence of velocity
float *div;

//density
float *d, *dold, *dtemp;
float *map;

//sources
float *sd, *su, *sv;

...

//
// Allocate memory for most arrays
//

...

// Initialize our "previous" values of density and velocity to be all zero
cudaMemset(uold, 0, size * sizeof(float));
cudaMemset(vold, 0, size * sizeof(float));
cudaMemset(dold, 0, size * sizeof(float));

// Host density copy, you can initialize this if you'd like, then copy it to dold
map = (float *) malloc(size * sizeof(float));

// Create the sources using some arbitrary source creation function
// that you wish to use
sd = create_source();
su = create_source();
sv = create_source();
Now, we can begin our main loop, putting all our kernels to good use: 
for(t = 0; t < steps; ++t) {

    //add sources to velocity (body force)
    add_source <<< blocks, THREADS_PER_BLOCK >>> (uold, su);
    add_source <<< blocks, THREADS_PER_BLOCK >>> (vold, sv);
    
    //add sources to density
    add_source <<< blocks, THREADS_PER_BLOCK >>> (dold, sd);
    
    //advect horizontal and vertical velocity components
    advect <<< blocks, THREADS_PER_BLOCK >>> (uold, u, uold, vold, 1);
    advect <<< blocks, THREADS_PER_BLOCK >>> (vold, v, uold, vold, 1);
    
    //advect density
    advect <<< blocks, THREADS_PER_BLOCK >>> (dold, d, u, v, 0.995);
    
    //call kernel to compute boundary values and enforce boundary conditions
    velocity_bc <<< blocks, THREADS_PER_BLOCK >>> (u, v);
    
    //call kernel to compute the divergence (div)
    divergence <<< blocks, THREADS_PER_BLOCK >>> (u, v, div);
    
    //reset pressure to 0 <- This is our initial guess to the Jacobi solver
    cudaMemset(p, 0, size * sizeof(float));
    
    //for each Jacobi solver iteration, 80 tends to be enough iterations to get convergence or close enough
    for (i = 0; i < 80; ++i)
    {
        //call kernel to compute pressure
        pressure <<< blocks, THREADS_PER_BLOCK >>> (u, v, p, pold, div);
        
        //swap old and new arrays for next iteration
        ptemp = pold; pold = p; p = ptemp;
        
        //call kernel to compute boundary values and enforce boundary conditions
        pressure_bc <<< blocks, THREADS_PER_BLOCK >>> (p);
    }
    
    //call kernel to correct velocity
    correction <<< blocks, THREADS_PER_BLOCK >>> (u, v, p);
    
    //call kernel to compute boundary values and enforce boundary conditions
    velocity_bc <<< blocks, THREADS_PER_BLOCK >>> (u, v);
    
	//copy density image back to host and synchronize
    cudaMemcpy(map, d, size * sizeof(float), cudaMemcpyDeviceToHost);
    cudaDeviceSynchronize();
    /*************************************************
     *                                               *
     *    Write to Image Here, Or Anywhere Really    *
     *                                               *
     ************************************************/
    
    //swap old and new arrays for next iteration
    utemp = uold; uold = u; u = utemp;
    vtemp = vold; vold = v; v = vtemp;
    dtemp = dold; dold = d; d = dtemp;
}
And that's a 2D fluid simulation based on the Navier-Stokes equation on the GPU! Like it was mentioned above, you can add diffusive effects to both the density and velocity giving the fluid some sense of viscosity and allowing the "ink" to disperse more realistically. One downfall of this method is that due to numerical error, you tend to lose the extra vorticity in the movement of the fluid, but you can restore this using vorticity confinement methods.
Overall, compared to traditional serial methods, this tends to run much faster, and the bottleneck still tends to be the writing of images as opposed to the actual calculations. If you would like to view the full source code, go to /u/mknyszek/cuda/nsflow and all the files should be there.

For some examples of what this simulation code has produced, take a look at these videos: Back to Top ➚


Debugging CUDA Code

Debugging CUDA code can seem daunting at first because at first it may seem almost impossible to look at values on GPU memory without first copying the values back to the CPU. Luckily, NVIDIA provides several methods for debugging CUDA code and handling errors.
Before you get started, for the most detailed results with NVIDIA CUDA debugging tools, make sure to compile your code with the -G flag in addition to the -g flag (which is the standard gcc flag for compiling with debugging information).

printf Usage

On newer GPUs (such as the ones we have at the lab) you can actually use printf statements in device code to find out values at a certain time. The only issue is that when a kernel runs, it cannot print out values in real-time. When using printf, be wary of the fact that anything printing will only appear after the kernel terminates. During kernel execution the string is shoved into a buffer which is then flushed at kernel termination. This can sometimes make debugging very tedious as you get inundated with statements printed to the command line simultaneously.

Of course, you can always isolate a certain thread and only print values from that thread, but in the end that can be a lot of wasted effort because the range of values you can see is now very narrow and it won't bring you to the root of the problem.

cuda-gdb

NVIDIA has developed an extension to gdb to help diagnose and eliminate bugs in CUDA programs. Simply run cuda-gdb in the same way you would run gdb, and cuda-gdb will give you a plethora of information about your program as its running, including kernel launches and any errors or warnings related to CUDA runtime functions.
cuda-gdb works identically to gdb and lets you view values in global memory as well as set breakpoints in your device code just as you would with any other C/C++ program.
While cuda-gdb can really save you a few hours of debugging your device code, it can sometimes act strangely with host code. It is recommended that when you have problems with your host code, stick to using only gdb as it is much more reliable.

cuda-memcheck

If you fear that your program is starting to do strange things with GPU memory and other memory errors are occurring that are not made obvious using cuda-gdb, NVIDIA has also provided another program called cuda-memcheck. Run it on your program by specifying your program as an argument to cuda-memcheck and it will generate a nice report if it finds any fatal memory errors.

HANDLE_ERROR Macro

Although NVIDIA includes a hefty error handling system for CUDA runtime subroutines, it can get very tedious to use for every single instance of a CUDA runtime function you wish to check.

This tool in particular is not a tool created by NVIDIA but rather by developers who use it to handle errors easily for the purposes of debugging. Simply define the following function and macro at the top of your file:

static void HandleError( cudaError_t err, const char *file, int line ) {
  if (err != cudaSuccess) {
    printf( "%s in %s at line %d\n", cudaGetErrorString( err ), file, line );
    exit( EXIT_FAILURE );
  }
}
#define HANDLE_ERROR( err ) (HandleError( err, __FILE__, __LINE__ ))

This macro now makes handling CUDA runtime errors very easy. Simply wrap your CUDA runtime functions with the macro like so:

HANDLE_ERROR( cudaMalloc((void **) &d, size * sizeof(float)) );

Back to Top ➚


Profiling CUDA Code

When your code is complete and working well, you may wish to identify bottlenecks in running time and optimize the code to squeeze out as much GPU performance as possible.
NVIDIA also has a pair of tools for profiling: one for the command line and one with an Eclipse-based GUI. Before using either of these tools, make sure you first compile your code with the -pg flag.

nvprof

This is NVIDIA's counterpart to the well-known C program profiler gprof. nvprof is excellent for performing quick profiling checks on your code to ensure that time is being expended where you expect it to. Its very lightweight and handy, and in addition can be run on any program that creates CUDA kernels. This even includes programs which use OpenACC or CUDA Python and it can be extremely helpful for determining where exactly a CUDA kernel is being launched and for what.

One particularly helpful flag for nvprof is --print-gpu-trace which prints a detailed GPU stack trace with all function calls, what GPU they are running on, and their dimensions.
Another helpful flag is --output-profile which generates a file detailing the profile, which can be later imported back into nvprof, or perhaps nvvp.

If you find that your program uses significant CPU time as well, using a combination of nvprof and gprof can give you a nice look into where the most time is being spent.

nvvp

nvvp is the NVIDIA Visual Profiler. Simply create a new session, specify the command line arguments and working directory of your properly compiled program, and it will generate very detailed reports regarding the performance of your program. There exist additional options to only profile certain portions of your program too, among other things. Those accustomed to Eclipse should find that this tool is very easy to use and incredibly useful.

Back to Top ➚


Tips & Tricks

Below is a collection of tips & tricks that have been mostly found through experience and can come in handy if/when CUDA C/C++ does not behave as expected. Back to Top ➚