Linear n=1 TAE structure and stability

Questions can be sent to N.N. Gorelenkov: ngorelen@pppl.gov.
We fix simple case with analytical plasma profiles

n=1, R₀=3m (major radius of the last closed surface), a=1m, circular, zero beta tokamak
equilibrium, q=1.1+psi where psi is a normalized poloidal flux varying from 0 at axis to 1
at the edge. Plasma density profile is constant. Equilibrium profiles are given in this file. In
this file all the variable notations are standard for Grad-Shafranov equation. F is normalized
in such way that B=1 at the geometrical center so that F=B*R/R0. Fp is its prime with the
regard of the poloidal flux, which is also presented.

Energetic ion parameters:
v_h/v_A =1.7
rho_h/a =0.085
EP beta profile ~ exp(-psi/0.37)

Distribution function is taken either Maxwellian or slowing down. In the latter case we have
f=1/(v**3+v_crit**3) * exp(-<psi>/0.37)
where velocities are normalized to the injection velocity v_h and
v_crit=0.58
Note that <Psi> in this expression is considered averaged over the particle guiding center orbit. In this case it is a function of particle constants of motion as it should be. One can show that for alpha particles the distribution function is a function of <Psi>. We used <Psi> computing the critical velocity and the scattering frequency. One simple and relatively accurate workaround of how to go from <Psi> to particle integrals of motion is following.
        If we define P_phi = e Psi /mc - v|| R, we find that for trapped particle with the accuracy up to ratio of the orbit width to the minor radius times epsilon^2 we have P_phi = e <Psi> /mc. For passing particles with the same accuracy we find P_phi = e*<Psi> /mc - sigma*v*sqrt( 1 -mu*B0/E )R0, where sigma is the sign of v||, B0 is the magnetic field at the center of the magnetic surface, and R0 is the major radius of the surface, mu is the adiabatic moment.

These parameters can correspond to deuterium plasma and EP mass and charge:
m_i = m_f = 2
z_i = z_f = 1

E_EP0 = 173keV
B₀     = 1T
ne     = 4.142 10¹³ cm^-3
Te     = 3.14 keV (used for v_crit value)

NOVA results for the TAE frequency are omega = 0.654 v_A/ q₁R₀ where q₁=q(a)=2.1.
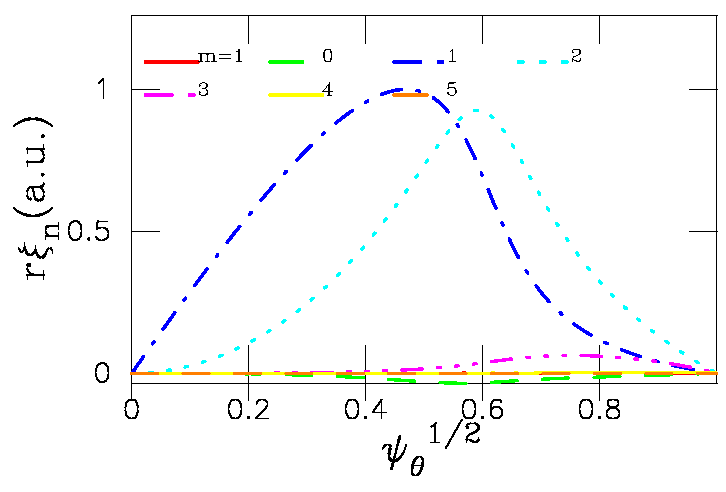
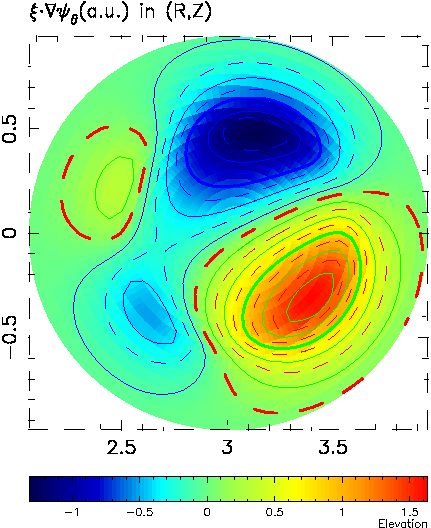
The structure of this n=1 TAE is shown as radial dependence of r times normal component of
the plasma displacement poloidal harmonics (below left) and the same function in R,Z plane (below right).
Dominant harmonics are saved for comparisons in this file for the case with the equal arc poloidal
angle choice and in this file for case with Boozer coordinates.

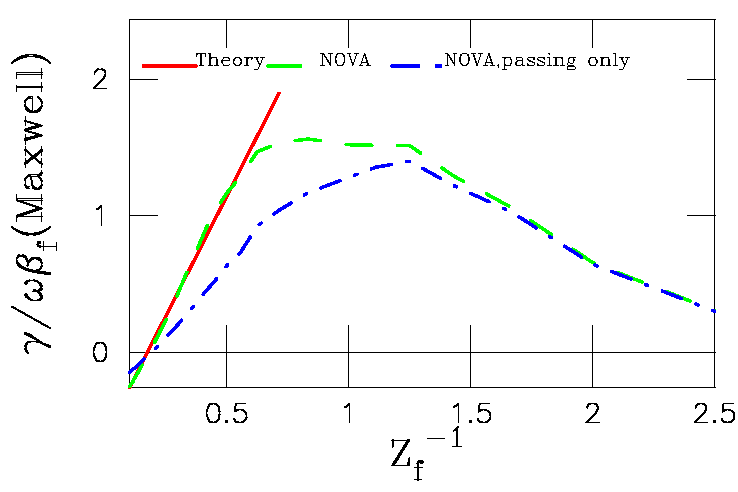
Stability properties are computed first with the Maxwellian distribution function of EPs.
Results are summarized in the following figure, where "effective" particles charge is changed
during the scan. Growth rates are normalized to fast ion beta in the center (beta=8pi pressure/B0^2,
where B0 is the magnetic field taken in the geometrical center of the plasma) is plotted against z_f^-1.
The data for the following graph (Maxwellian distribution) are in this file. The data structure used in
this file is presented via 5 columns as follows:

zi cogoing countergoing total_NOVA total_theory

For slowind down similar scan produces following dependencies:

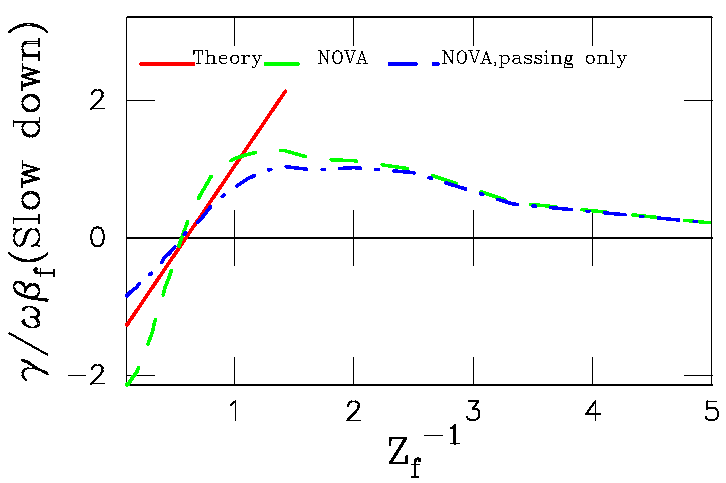
In the latter case theory curve was obtained for the model distribution function with some v_crit term. Thus
there is some disagreement. It is much better agree with theory for n=2 case and slowing down distribution.
Theoretical expressions are derived for zero orbit EPs. The expressions are documented in this FILE.