


Next: Effect of Magnetic Islands
Up: Quasi-linear Tearing Mode Equations
Previous: Summary of the derivation
At each mode rational surface, 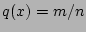 , the expression
, the expression
goes to zero, thus giving the appearance that equations
(8) and (10) are singular at mode rational
surfaces. However, the existence of a magnetic island or
stochastic region, which is implied by a nonzero 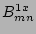 at the mode rational surfaces, locally flattens the
at the mode rational surfaces, locally flattens the 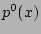 and
and
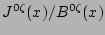 profiles. This removes the
singularity in Eqs (8) and (10)
[3,8] as is shown in the
subsection below. The perturbation affects the background
profiles and permits a saturated island solution, in contrast to a
linear tearing mode solution.
profiles. This removes the
singularity in Eqs (8) and (10)
[3,8] as is shown in the
subsection below. The perturbation affects the background
profiles and permits a saturated island solution, in contrast to a
linear tearing mode solution.
Consider a stream function 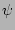 that is uniform along magnetic
field lines:
that is uniform along magnetic
field lines:
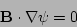 |
(26) |
If 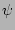 is a smooth function with a local minimum at the mode
rational surface, the Taylor series for
is a smooth function with a local minimum at the mode
rational surface, the Taylor series for 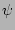 that satisfies Eq.
(26) yields
that satisfies Eq.
(26) yields
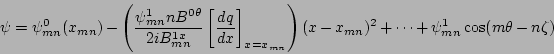 |
(27) |
where 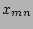 is the radius of the mode rational
surface and where
is the radius of the mode rational
surface and where
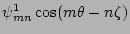 is the
lowest order harmonic perturbation. With the value of
is the
lowest order harmonic perturbation. With the value of 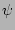 at
the edge of the widest part of the island (
at
the edge of the widest part of the island (
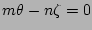 ,
,
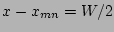 ) set equal to the value of
) set equal to the value of 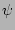 at the x-point
(
at the x-point
(
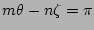 ,
, 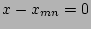 ), the following equation
for the width of the island is obtained
), the following equation
for the width of the island is obtained
![\begin{displaymath}
W_{mn}=4\sqrt{\left[\frac{-iB^{1x}_{mn}}{nB^{0\theta}(dq/dx)}
\right]_{x=x_{mn}}}
\end{displaymath}](img81.png) |
(28) |
Higher order terms in the Taylor series (27)
may be used to determine the asymmetry in the island width and
other details of the island's shape. Note that the island width
is measured in terms of the flux surface label 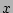 . The geometrical
width of the island may vary poloidally around a flux surface, being
wider where the background flux surfaces are more spread apart and
narrower where the background flux surfaces are squeezed together.
This effect is automatically taken account when using flux coordinates.
. The geometrical
width of the island may vary poloidally around a flux surface, being
wider where the background flux surfaces are more spread apart and
narrower where the background flux surfaces are squeezed together.
This effect is automatically taken account when using flux coordinates.



Next: Effect of Magnetic Islands
Up: Quasi-linear Tearing Mode Equations
Previous: Summary of the derivation
transp_support
2008-12-08
![]() that is uniform along magnetic
field lines:
that is uniform along magnetic
field lines:
![]() is the radius of the mode rational
surface and where
is the radius of the mode rational
surface and where
![]() is the
lowest order harmonic perturbation. With the value of
is the
lowest order harmonic perturbation. With the value of ![]() at
the edge of the widest part of the island (
at
the edge of the widest part of the island (
![]() ,
,
![]() ) set equal to the value of
) set equal to the value of ![]() at the x-point
(
at the x-point
(
![]() ,
, ![]() ), the following equation
for the width of the island is obtained
), the following equation
for the width of the island is obtained
![]() . The geometrical
width of the island may vary poloidally around a flux surface, being
wider where the background flux surfaces are more spread apart and
narrower where the background flux surfaces are squeezed together.
This effect is automatically taken account when using flux coordinates.
. The geometrical
width of the island may vary poloidally around a flux surface, being
wider where the background flux surfaces are more spread apart and
narrower where the background flux surfaces are squeezed together.
This effect is automatically taken account when using flux coordinates.