Multi-Mode Transport Model MMM95 Version 1.1


Glenn Bateman, Arnold H. Kritz
Lehigh University Physics Department
16 Memorial Drive East, Bethlehem PA 18015
bateman@plasma.physics.lehigh.edu
kritz@plasma.physics.lehigh.edu

This file documents a subroutine called mmm95, which computes plasma transport coefficients using the Multi-Mode transport model which has been held fixed since 1995. A complete derivation of the MMM95 model is given in reference [1]. Note, the mmm95 subroutine has been tested and used when compiled with flags such that double precision is used. Note also, if this module is used in another code, the minimum dimension required for cswitch is 23, the minimum dimension for lswitch is 5 and fig, frb, and fkb must all be dimensioned to a minimum of 4.

When sbrtn mmm95 is used in the BALDUR transport code to compute particle and thermal fluxes, smoothing of the gradients is normally needed for numerical stability. Note that the lower bounds of the gradient scale lengths are limited by the poloidal ion Larmor radius (zlarpo) in sbrtn mmm95.

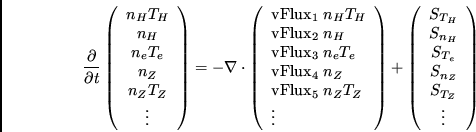
The full matrix form of anomalous transport has the form

$$\frac{\partial}{\partial t} \left( \begin{array}{c} n_H T_H ... ...S_{T_e} \\ S_{n_Z} \\ S_{T_Z} \\ \vdots \end{array} \right)$$

$$= \nabla \cdot \left( \begin{array}{llll} D_{1,1} n_H & D_{... ...H \\ n_H \\ T_e \\ n_Z \\ T_Z \\ \vdots \end{array} \right)$$

$$+ \nabla \cdot \left( \begin{array}{l} {\bf v}_1 \; n_H T_H... ...S_{T_e} \\ S_{n_Z} \\ S_{T_Z} \\ \vdots \end{array} \right)$$

Note that all the diffusivities are in units of m$^2$/sec while the convective velocities and vfluxes are in units of m/sec.

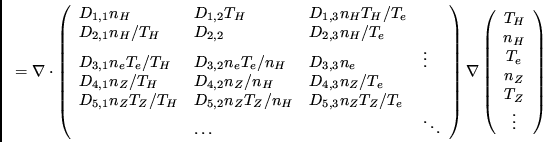
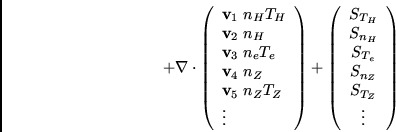
WARNING: Do not add separate convective transport terms to this anomalous transport model. All the anomalous transport predicted by this Multi-Mode model is contained in the diffusion coefficients difthi and velthi given above.

We then enter a loop over the spatial zones, and establish local variables for all the input arrays for more compact notation.

To complete the rest of the calculation we then compute various quantities needed for the transport flux formulas (as in Table 1 of the Comments paper, from which $\omega_{ce}$ was inadvertantly omitted). To begin with, we compute only quantities which do not involve scale heights. In the order in which they are computed, algebraic notation for these quantities is:

$$\omega_{ci}=eB_{o}/(m_{p}A_{i}) \eqno{\tt zgyrfi}$$

$$\beta=(2\mu_{o}k_{b}/B_{o}^{2})(n_{e}T_{e}+n_{i}T_{i}) \eqno{\tt zbeta}$$

$$v_{e}=(2k_{b}T_{e}/m_{e})^{1/2} \eqno{\tt zvthe}$$

$$v_{i}=(2k_{b}T_{i}/m_{p}A_{i})^{1/2} \eqno{\tt zvthi}$$

$$c_{s}=[k_{b}T_{e}/(m_{p}A_{i})]^{1/2} \eqno{\tt zsound}$$

$$\ln (\lambda)=37.8 - \ln (n_{e}^{1/2}T_{e}^{-1}) \eqno{\tt zlog}$$

$$\nu_{ei}=4(2\pi)^{1/2}n_{e}(\ln \lambda)e^{4}Z_{eff} /[3(4\p... ...silon_{o})^{2}m_{e}^{1/2}(k_{b}T_{e})^{3/2}] \eqno{\tt znuei}$$

$$\eta=\nu_{ei}/(2\epsilon_{o}\omega_{pe}^{2}) \eqno{\tt zresis}$$

$$\nu_{eff}=\nu_{ei}/\epsilon \eqno{\tt znueff}$$

$$\nu_{e}^{*}=\nu_{ei}qR_{o}/(\epsilon^{3/2}v_{e}) \eqno{\tt thnust}$$

$$\hat{\nu}=\nu_{eff}/\omega_{De} \eqno{\tt znuhat}$$

$$\rho_{\theta i}=\rho_{i}q/\epsilon \eqno{\tt zlari}$$

$$\rho_{i}=v_{i}/\omega_{ci} \eqno{\tt zlarpo}$$

$$\rho_{s}=c_{s}/\omega_{ci} \eqno{\tt zrhos}$$

$$k_{\perp}=0.3/\rho_{s} \eqno{\tt zwn}$$

The corresponding coding is:

Our formulas for the shear begin with

$${\hat s}_{cyl}=\vert(r/q)(\partial q/\partial r)\vert \eqno{\tt zscyl}$$

computed earlier in this subroutine. The minimum prescribed shear is

$${\hat s}_{min}=max(c_{1},0) \eqno{\tt zsmin}$$

where $c_1=$ = cswitch(1) so that shear is then given by

$${\hat s}=max({\hat s}_{min},{\hat s}_{cyl}) \eqno{\tt zshat}$$

The relevant coding for the calculations just described is: