


Next: Thermal Conduction Model II
Up: H-mode temperature model
Previous: Model with width based
This model is given by Eq. (2) in Ref. [8]. If the pedestal stored energy, 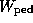 , is known, the pedestal temperature can be found as
, is known, the pedestal temperature can be found as

where V is the plasma volume. Note that the constant of 0.92 is the fraction of the total volume occupied by the pedestal [7]. The plasma volume can be estimated as

By fitting to all types of ELMy H-mode discharges in the pedestal database DB3V2 [8], it was found that the pedestal stored energy is
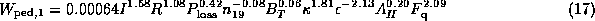
where I is the plasma current in unit of MA, 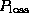 is the loss power in unit of MW,
is the loss power in unit of MW, 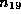 is the density in the unit of 1019 particles per m3,
is the density in the unit of 1019 particles per m3,  is the inverse aspect ratio and
is the inverse aspect ratio and 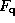 is the shaping factor (
is the shaping factor (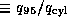 , where q95 is the safety factor at 95% flux surface and
, where q95 is the safety factor at 95% flux surface and 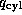 is the cylindrical safety factor defined as
is the cylindrical safety factor defined as 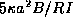 ). This formula yields the RMSE of 23.5% with the data [8]. This scaling satisfies both the Kadomtsev and the gyro-Bohm constraints with
). This formula yields the RMSE of 23.5% with the data [8]. This scaling satisfies both the Kadomtsev and the gyro-Bohm constraints with 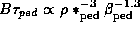 .
.
By combining Eqs.  ,
,  and
and  , the pedestal temperature in unit of keV can be found as
, the pedestal temperature in unit of keV can be found as
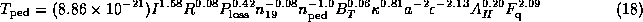
transp_support
Wed Apr 2 12:00:26 EST 2003