Oct 14, 1997
I don't see the point of doing the R/L_T=2 and 3 points. The real question is: Do the GF errors near threshold affect the GF results above threshold? If the R/L_T=2 and 3 points fall on the line (which seems likely), we have not answered this question. We know these points will give finite chi, while the real answer is zero. But this does not show whether or not these errors affect the results well above threshold.
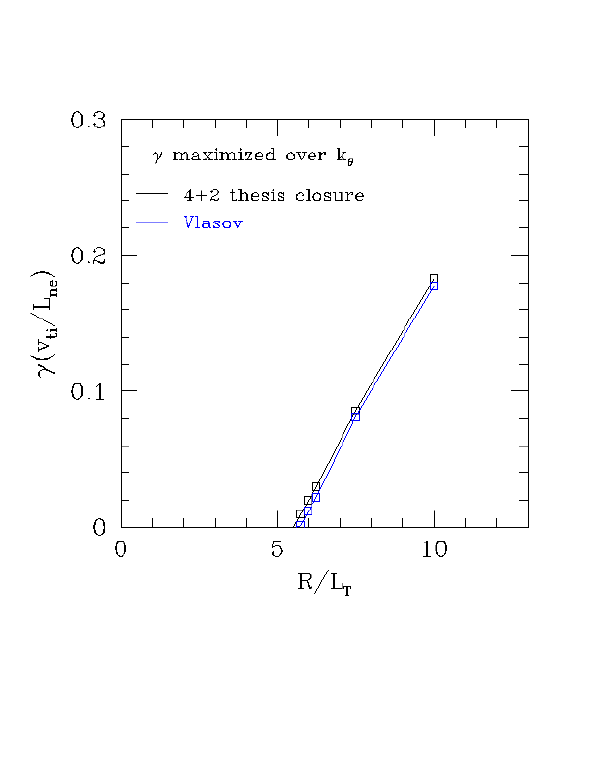
Instead, I've been looking for a place where the GF threshold is right on, to see if the GF/GK chi discrepancy remains. I just found such a point: the NTP parameters with epsilon=0. The GF thesis closure gets the threshold very close to what I found with the Vlasov code, as shown below.

At the NTP point (R/L_T=10), the GF linear growth rates are in very good agreement with kinetic theory, as shown below.
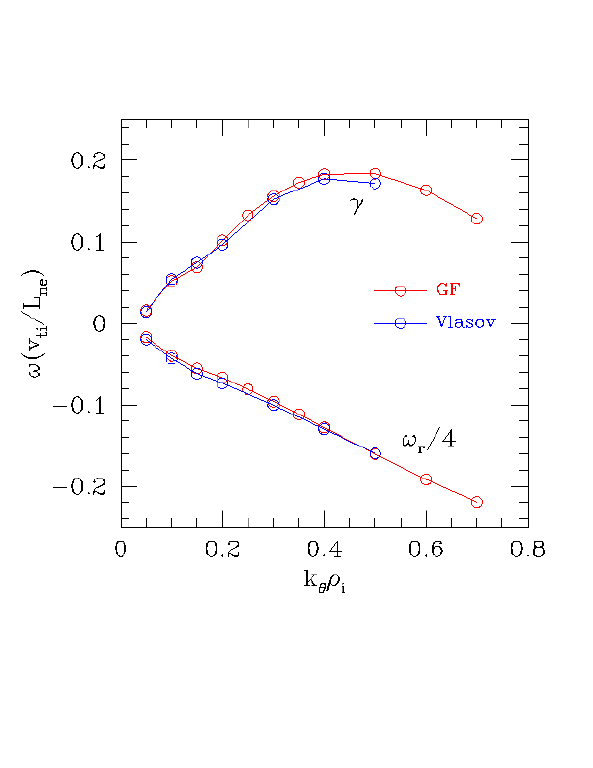
We already have nonlinear runs for this case: the chi's are the epsilon=0 points on this page. Even though the GF thesis R/L_Tcrit is right on, the GK chi is 2x lower than the GF chi. Thus in this case, GF linear errors near threshold are not causing the discrepancy in chi. The agreement here (2x) is better than the DIII-D base case (3x), so if other factors account for this 2x difference, perhaps the GF linear errors are at most accounting for 1.5x of the difference for the DIII-D base case.
It might be useful for someone to run the epsilon=0 NTP case with Andris's parallel code. The results I'm comparing are from IAEA '94.
--Mike.
Back to index of cyclone pages
Back to Mike Beer's home page