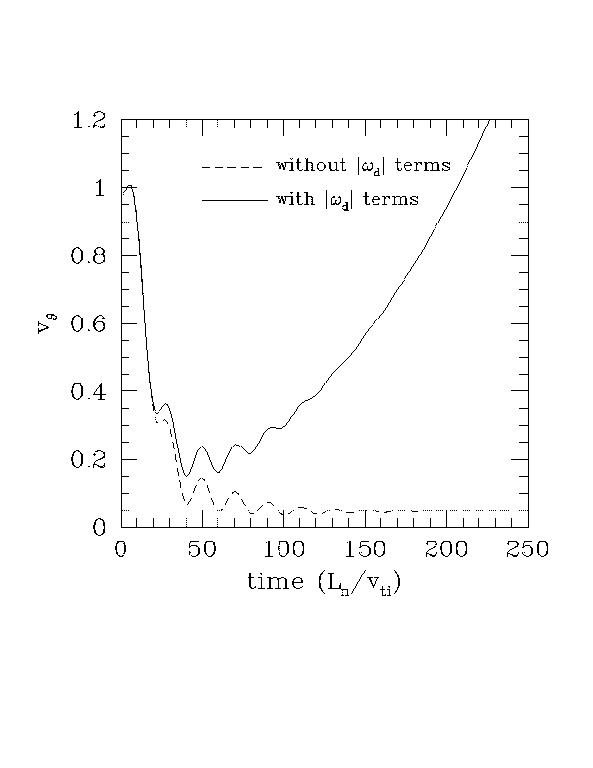
Last week, Marshall sent some comments on poloidal flow damping in gyrofluid simulations. I've put the results of a preliminary nonlinear test of this issue below.
(More recent results can also be found here--9/15/97.)
---------------------------------
March 2, 1997
In Sec. 5.3 of my thesis, I showed that the toroidal gyrofluid equations properly model poloidal flow damping for times less than a bounce time, and hypothesized that recovering this short-time limit of the poloidal damping was adequate for turbulent situations, even though the long-time limit is incorrect. Here, I test this hypothesis. In the collisionless limit, the long time behavior (e.g. the steady state in Fig. 5.11 in my thesis) of the gyrofluid equations is determined by the dissipative |omega_d| closure terms in the evolution equations of the higher moments (p_par, p_perp, q_par, q_perp). After the initial transient dies away, these dissipative terms will slowly damp the residual rotation. In real life, this long-time behavior will be determined by trapped particle dynamics and collisions (MNR & FLH), so the gyrofluid equations do not get this right. The issue is whether it is the long-time linear behavior or the short-time linear behavior which sets the amplitude of the poloidal rotation and the turbulence levels.
We can test this by changing these dissipative |omega_d| terms to change the long-time behavior. To take an extreme case, in Figure 1 I use a set of closure coefficients different than those used in my thesis, which actually lead to a weakly growing(!) poloidal rotation in the long-time limit, but in all other respects are quite reasonable, i.e. they give good linear growth rates for m.ne.0. Figure 2 also shows the poloidal rotation with the dissipative |omega_d| terms turned off for the m=0 modes, where the long-time behavior is constant, as in Fig. 5.11 of my thesis. Thus these two cases, with and without the |omega_d| terms for the m=0 modes, give very similar damping rates for short times, but extremely different behavior for long times.
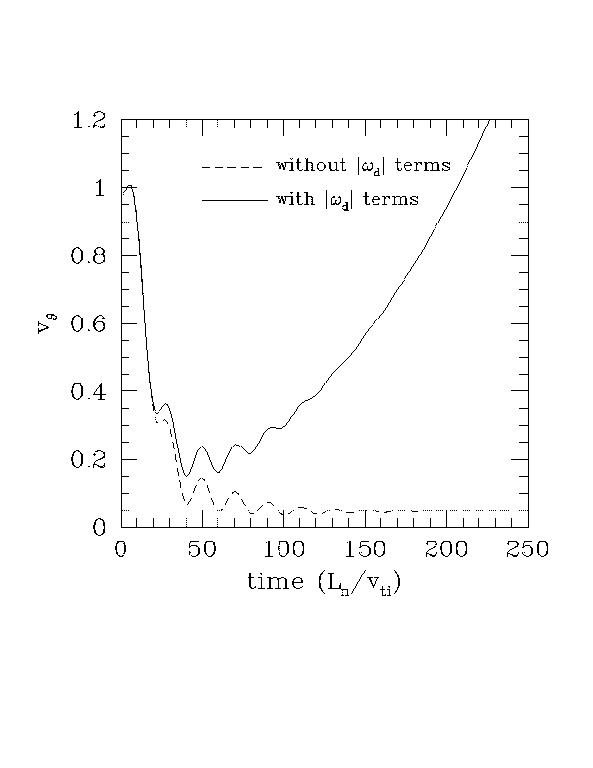
Figure 1: Flow damping with and without dissipative |omega_d| terms, for k_r rho_i=0.07.
Using these closure coefficients, Figure 2 shows two nonlinear simulations, with identical parameters in every respect except that in one, we retain the |omega_d| terms for the m=0 modes, but in the other we turn off the |omega_d| terms for the m=0 modes only, i.e. m.ne.0 modes are treated identically. If the long-time limit of the damping dominates, in the case with the |omega_d| terms, the poloidal rotation should slowly grow to large amplitudes and strongly reduce the flux. If the short-time limit of the damping dominates, the two cases should have very similar poloidal rotation levels and similar flux. Figure 2 shows that these two cases give very similar results, indicating that the short-time limit of the damping sets the poloidal rotation levels. In fact, the case without the |omega_d| terms gave slightly less flux, but I think this is within the statisical fluctuations. I'd like to do higher resolution runs and compare the rotation levels directly to be definite about this, but the result of this test strongly indicates that the long-time limit of the damping is not dominant.
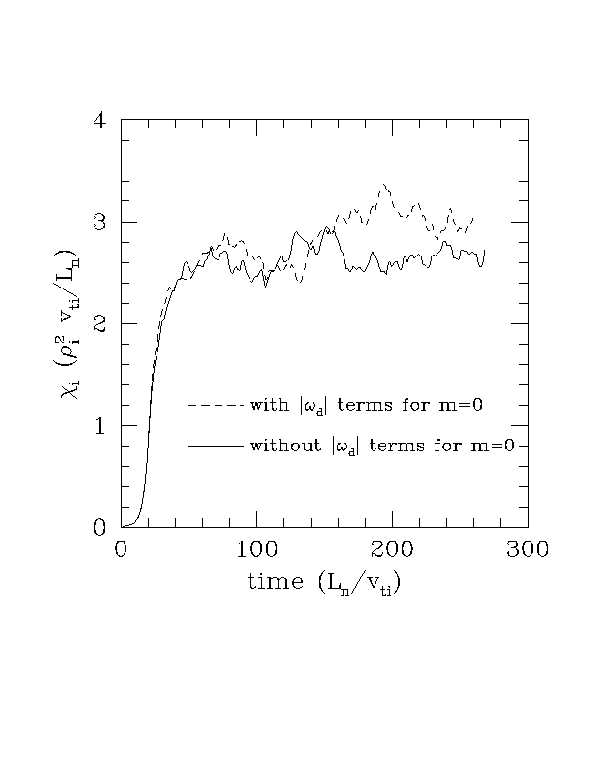
Figure 2: Nonlinear simulations with and without dissipative |omega_d| terms for the m=0 modes.
Note that in Fig. 5.7 of my thesis, all omega_d terms were turned off for m=0 modes, which also removes the short-time damping of the poloidal rotation (with omega_d=0 there are no toroidal effects). In this case, the rotation did grow to much higher levels, and the flux dropped dramatically.
Back to index of cyclone pages
Back to Mike Beer's home page