Nonlinear gyrofluid test cases

Sept 4, 1997

I have two results to report this week:

1. Plots of RMS Phi vs. time to compare with Andris's results.

2. Chi vs. epsilon (r/R) scaling to compare with Andris's IAEA epsilon scaling. (More recent results can also be found here--9/15/97.)

--------------------------------

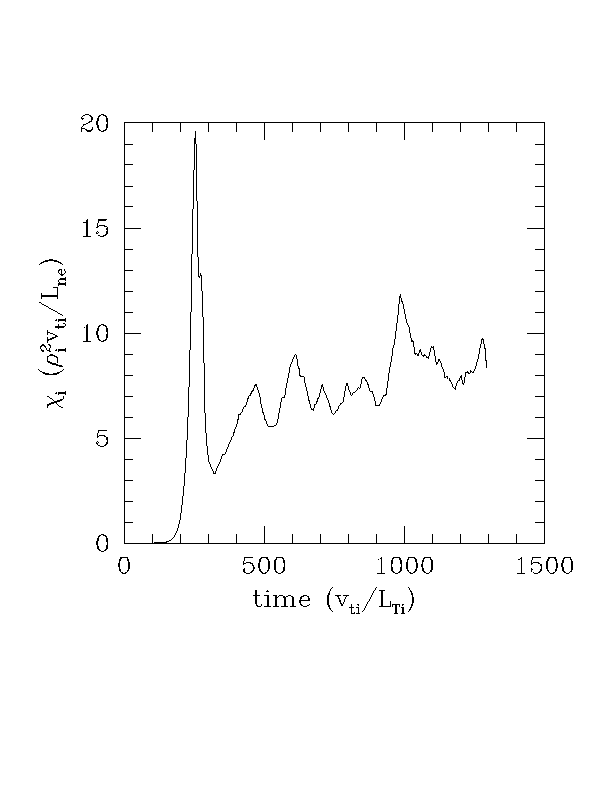
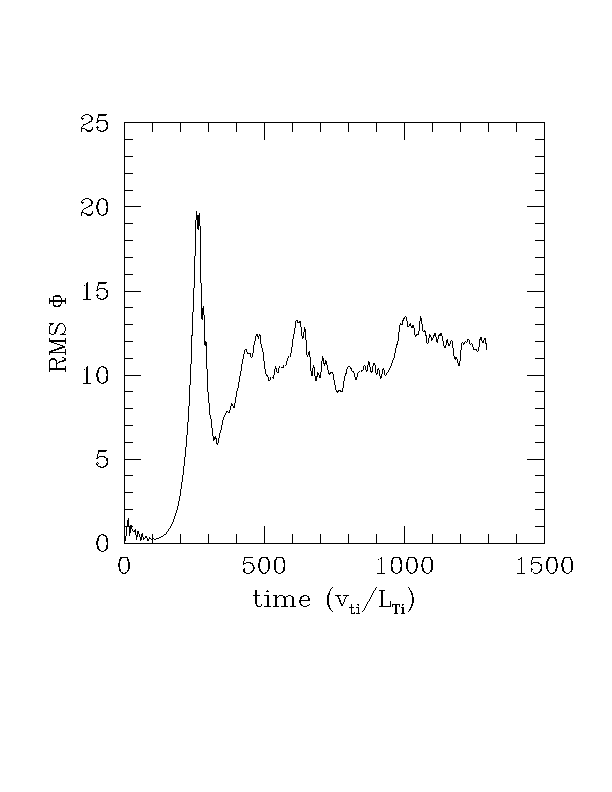
1. Below are plots of chi_i and the RMS Phi (volume averaged) for the base case parameters.

The RMS Phi agrees fairly well with Andris's value before Andris's RMS Phi starts getting spikey later in the run--but our chi_i is about a factor of 3 higher than Andris's result:

DIII-D base case:	k_theta,max	gamma	omega_r	R/L_Tcrit	chi_i	phi^2
GF Gryffin					8	12
GK particle					2.4	10

-----------------------------

2. As discussed previously, the epsilon (r/R) scaling of the comparison between GF and GK results can test the importance of the Hinton-Rosenbluth effect. Below I have done a set of runs to compare with Andris's IAEA paper, which has an epsilon scan in Figure 2. The time histories are shown below:

These runs used our "4+2" equations and a parallel box length of -pi to pi, the same as in the GK particle runs. We typically see a 40% increase with longer boxes, but haven't run these particular cases with longer boxes.

Because with larger epsilon energy goes to longer wavelengths, the boxes I used are not very good for eps=0.2 and eps=0.4. This is why these runs haven't settled down too well yet. The following is a comparison of Andris's scaling and these runs, with error bars on the GF points since the runs aren't totally saturated.

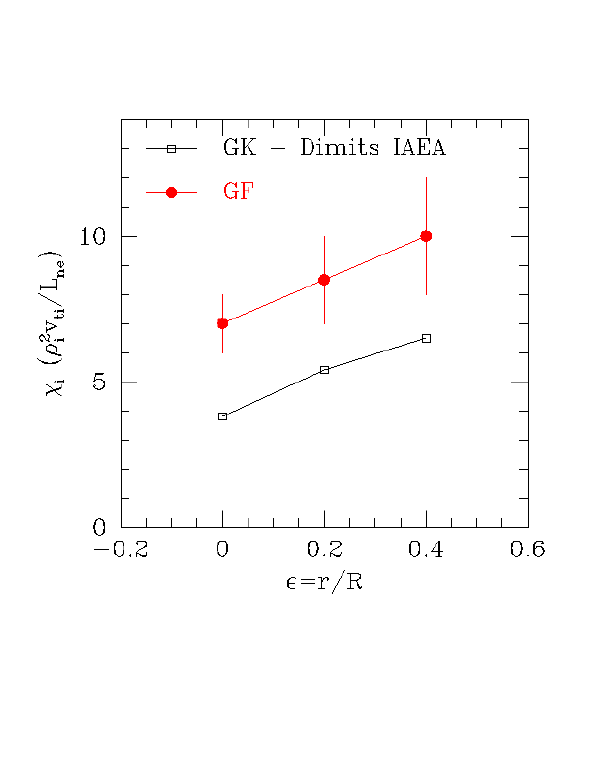
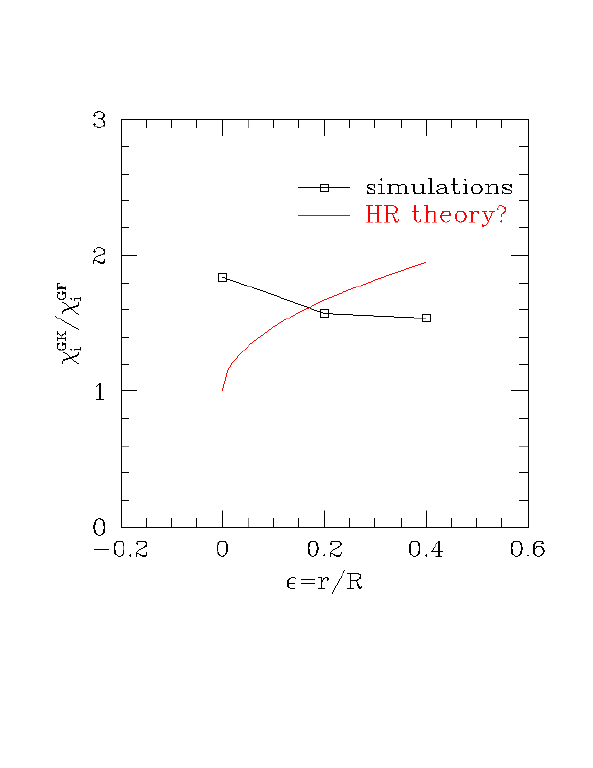
The trend is pretty clear: the difference between GF and GK does not scale strongly with epsilon. If the Hinton-Rosenbluth effect were the dominant cause of the difference between the GF and GK results, chi_GF/chi_GK would scale something like 1+const*sqrt(eps), as shown below in red.

--Mike

Back to index of cyclone pages
Back to Mike Beer's home page