Nonlinear n=4 core localized TAE saturation

(Questions/comments/suggestions should be sent to N.N. Gorelenkov: ngorelen@pppl.gov)

Here we document a TFTR case, published earlier, based on shot #103101. This case was used for
single core localized TAE (cTAE) mode saturation in the paper by Gorelenkov, et.al, PoP 6 (1999) 629.
Observations of TAEs (including n=4 mode) in these plasmas were reported in Nazikian, et.al, PRL 78
(1997) 2976, and Nazikian, et.al., Phys.Plasmas 5 (1998) 1703.

The choice for localized TAE solution was made due to its simplicity. The mode consist just of two most dominant
poloidal harmonics. Such a solution is known to exist in the low magnetic shear region near the center.

We fit plasma profiles into the analytic forms (close to the experimental profiles) for easier benchmark. The profiles were
fitted with the least square method from the TRANSP run for TFTR 103101 at t=2.92sec (see Nazikian's papers above).

It is important to emphise that the mode saturation is due to fast ion distribution function broadening near the resonance
in the presence of fast ion collisional scattering and background damping. The scattering is a key element of pysics to
have in the code, but other form of the collisional operator should also result in the saturation, but may have different saturation
amplitudes (see some of Berk's papers). The damping mechanism is not specified. Its absolute value is varied to see the trend
of the mode saturation amplitude vs. gamma_linear / gamma_damping.

NOTE, depending on which code is used it maybe required to simplify this case. What can be envisaged is fixing the
collisional scattering frequency and fixing critical velocity for the distribution function. These things are easy to add.
So far following is the set of plasma paramters used in the above mentioned paper for cTAE saturation.

1) Equilibrium is set up by specifying plasma pressure and q profiles.

R₀=2.53m, a=0.88m, B0=5.1T in the vacuum at the geometrical center. Plasma is circular,
total equilibrium pressure is such that
beta_total(r) = 0.01 (1- Psi^0.8)^2.7,
where beta_plasma is plasma pressure ratio to the magnetic field pressure taken at vacuum B=B0
at the geometrical center of the plasma, Psi is the poloidal flux normalized to its edge value, so that
Psi=0 in the center and Psi=1 at the edge.

q-profile has a specific form, which may seem weird but turns out to be very good in
approximating experimental profiles:
q(0)=1.6, q(1)=5, q'(0)=0, q'(1)=9.8,
q(r)=q(0) + Psi [ q(1) - q(0) + ( q'(1) - q(1)+q(0) ) (1-Psi_s)(Psi-1)/(Psi-Psi_s) ]
Psi_s=[ q'(1) - q(1) + q(0) ] / [ q'(0) + q'(1)- 2 ( q(1)-q(0) ) ],
where prime means derivative over Psi (see also CZ. Cheng, Phys.Reports 211 (1992) p.1).

Following is an additional information, important for the saturation mechanism since it is included
in the collisionality. It was DT plasma with dominant D density.

Density profiles are required for mode structure simulations
n_D = 1.8 *10^13 (1.-0.75 Psi^0.74)^1.13 cm^-3
n_T = 0.52*10^13 (1.-0.75 Psi^0.74)^1.13 cm^-3
n_H = 0.38*10^13 (1.-0.75 Psi^0.74)^1.13 cm^-3
n_Carbon = 0.18*10^13 (1.-0.75 Psi^0.74)^1.13 cm^-3
n_e     =   4. 10^13 (1.-0.75 Psi^0.74)^1.13 cm^-3
Z_eff = 2.44 (important for collisional scattering)
Note, that not all the codes have that many thermal ion species, but this is what was in the paper.
Since the ion density affects only Alfven velocity in this problem for the simplified version of the
benchmark we suggest single specie plasma density and
n_D = 3.85 *10^13 (1.-0.75 Psi^0.74)^1.13 cm^-3
n_e     =   4. 10^13 (1.-0.75 Psi^0.74)^1.13 cm^-3
but still require that Z_eff = 2.44.
Such simplified plasma produces the same results for the mode growth rate, frequency and saturation.
Since the collisional scattering is a key factor here we have to be on the same page. We use more accurate
collisional frequency as described in [R. Goldston, et.al. J. Comput. Phys. 43 (1981) p.61]. It is important
that the velocity dependence of the collisional frequency is retained.

Temperature of ions and electrons
T_i = 11.26 (1.-0.5 Psi)^5.5 keV,
T_e =      6. (1.-0.5 Psi)^5.5 keV.

2) Mode structure is obtained within ideal MHD NOVA model

cTAE mode frequency is omega = 1.47 v_A/ q(1)R₀. This frequency corresponds to the mode frequency 233.6kHz
(slightly higher than in the above paper due to the choice of analytical profiles).
Continuum is presented below (left) as omega^2 vs sqrt(Psi). One can see that we ignored the compressibility
by allowing gamma=0. This should allow for wider range of codes for the benchmark.

The structure of this mode is shown as poloidal harmonics (few dominant harmonics are shown) radial dependence
of r=sqrt(Psi) times normal component of the plasma displacement vs. sqrt(Psi) (right figure):

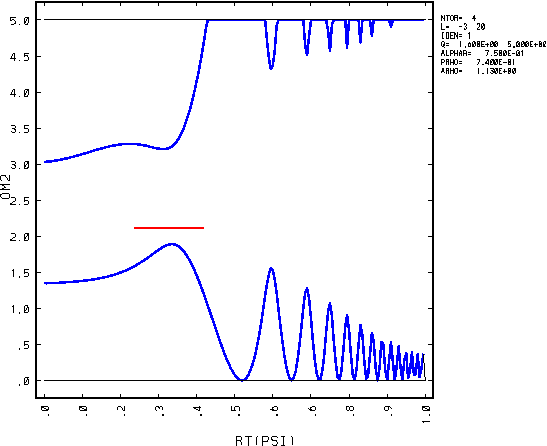
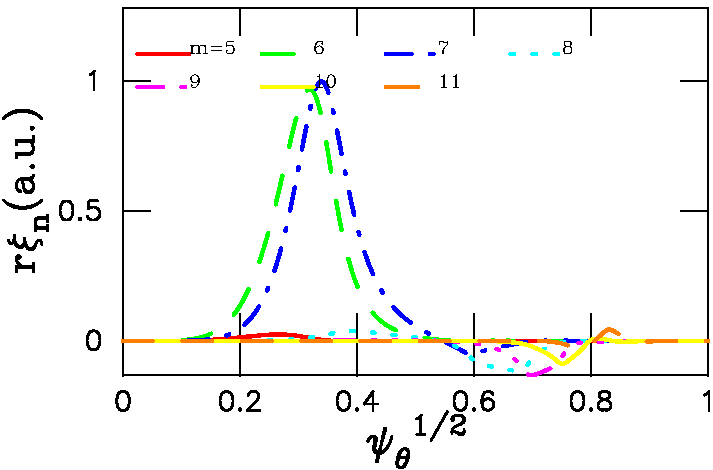
There are other TAEs, which we do not show. They should have smaller growth rate than the mode we show with the
peaked alpha particle profiles, so that in the initial value codes this cTAE mode is expected to grow first.

3) Stability is studied for alpha-particles with slowing down distribution function.
In order to help codes benchmarks we have two following "sub-cases" run, which produce essentially the same results for the nonlinear mode saturation. Actual figure and ORBIT results are shown for the following case 1).
Alpha particle parameters:
1) this "sub-case" is actually reported in the abovementioned my paper
E0=1.5MeV, v_alpha = 0.55*10^9 cm/sec,
    growth rate gamma/omega = 1.% with finite orbit width (FOW) and =~0.6% with extra alphas FLR effects added.
2) this "sub-case" produces almost identical saturation level figure (see below)
    E0=3.52MeV, v_alpha = 1.3*10^9 cm/sec,
    growth rate gamma/omega = 1.1% with finite orbit width (FOW) and =~0.8% with extra alpha FLR effects added.

other used parameters, imporant for the stability were
v_A = 1.27*10^9 cm/sec,
m_alpha = 4 m_proton,
z_alpha = 2 z_proton,
beta_alpha = 0.00083 exp[ - ( sqrt(<Psi>)/0.42 )^2.55 ] .
Note that <Psi> in this expression should be considered as averaged over the particle guiding center orbit. In this case it is a function of particle constants of motion as it should be. One can show that for alpha particles the distribution function is a function of <Psi>. We used <Psi> computing the critical velocity and the scattering frequency. One simple and relatively accurate workaround of how to go from <Psi> to particle integrals of motion is following.
        If we define P_phi = e Psi /mc - v|| R, we find that for trapped particle with the accuracy up to ratio of the orbit width to the minor radius times epsilon^2 we have P_phi = e <Psi> /mc. For passing particles with the same accuracy we find P_phi = e*<Psi> /mc - sigma*v*sqrt( 1 -mu*B0/E )R0, where sigma is the sign of v||, B0 is the magnetic field at the center of the magnetic surface, and R0 is the major radius of the surface, mu is the adiabatic moment.

We find that the growth rate due to alphas is gamma/omega = 1.01% with finite orbit width effects but ingnoring
FLR effects, and =~0.6% with FLR effects. This is slightly lower than previously reported due to fitted
plasma profiles, rather than inputed from TRANSP.

4) cTAE amplitude saturation
Following is the same figure as in the paper but plotted in log scale for the perturbed poloidal field in saturation. In
plotting these results we used maximum value of the poloidal magnetic field over the mode 2D structure. The procedure
of how we computed this value is described in the abovementioned paper by Gorelenkov.

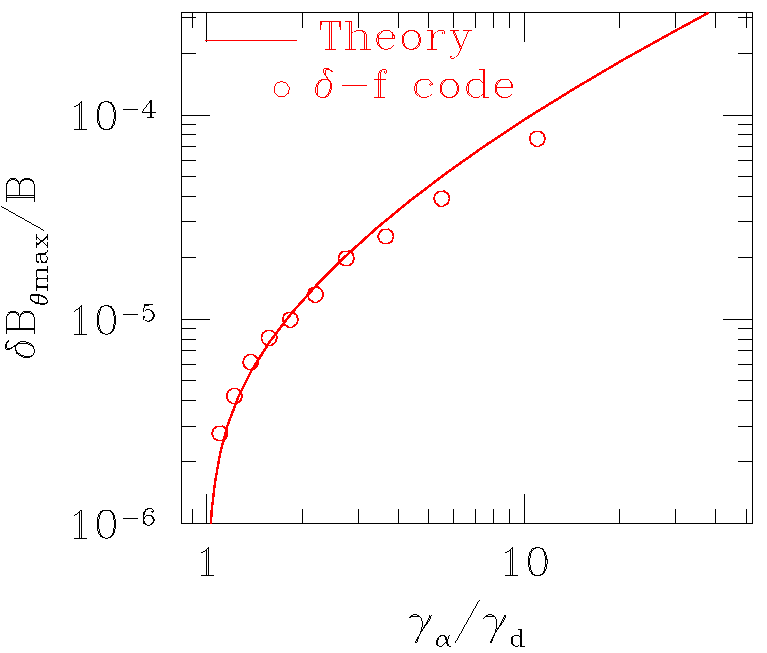
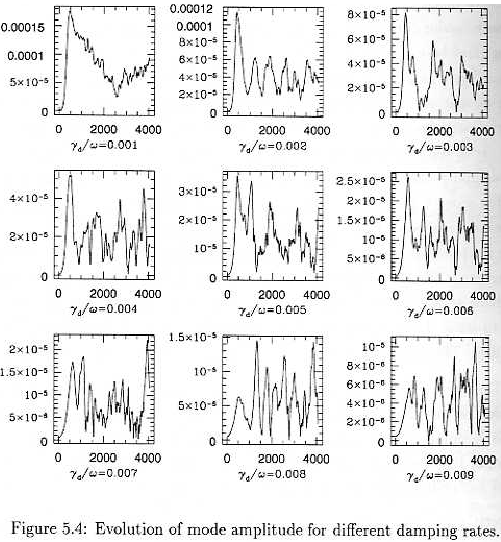
Delta f code used is referenced in my paper above. Following figures from Y. Chen thesis
illustrate the evolution of the magnetic field in that code for the case just described. Note,
that in those runs growth rate was fixed gamma_alpha/omega = 1.1%, which is close to our
results.

5) Trapped (in the wave field) frequency of the dominant resonance
Here we single out the dominant (fundamental v||=v_A) alpha particle resonance at the maximum of mode amplitude
and compute the frequency of a particle trapped in the field of TAE mode as a function of mode amplitude.
We use NOVA-K and ORBIT codes to compute the trapping frequency.
Resonant particle has following parameters v/v0 = 0.718, <psi/psi0> = 9.67e-2, psi/psi0 = 0.11 at Z=0,R=2.867m,
v||/v=0.593 in NOVA-K and v||/v=0.62 in ORBIT, v0 corresponds to E=3.52MeV. Note, that there is small
difference in v||/v in both codes. v||/v was adjusted to get the same psi/psi0 = 0.11 at Z=0,R=2.867m at to ensure that
orbits look the same in both codes.
Following figure shows the trapped orbits from ORBIT code in the plane, which horizontal axis is (omega + n phi) and vertical axis is particle (psi/psi0) at the LFS of the midplane intersection with the particle orbit. Orbits are plotted for deltaB/B=10^-5.

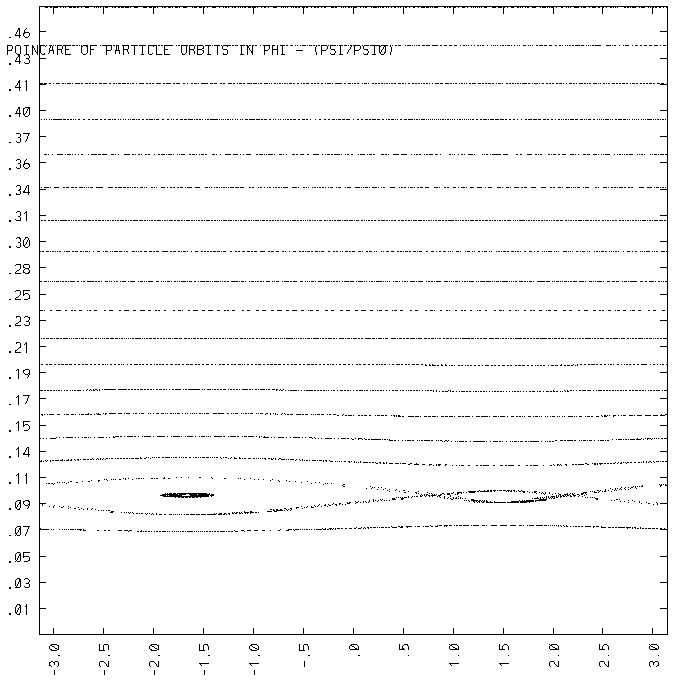
Next plot shows trapping frequency for the deepest trapped particle of the figure above as function of mode amplitude.
The results are obtained again using NOVA-K and ORBIT codes as indicated.

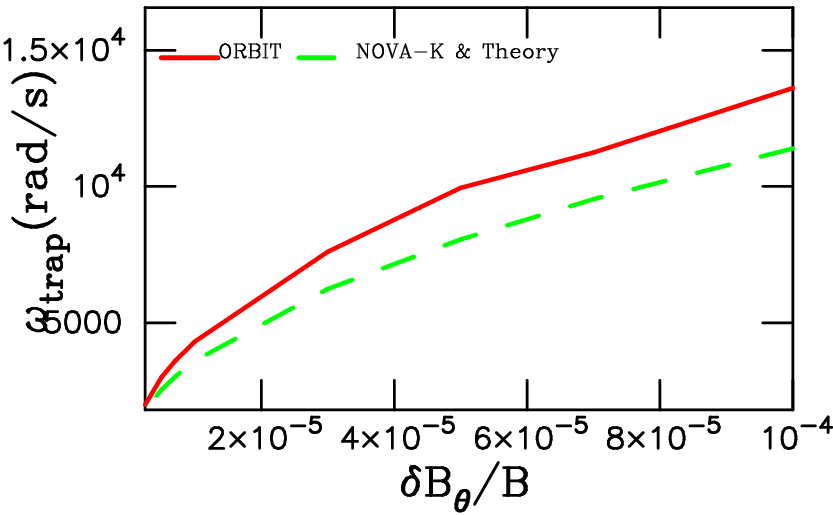
Note, that to help this benchmark there will be more installments, such as trapping frequencies and other
useful information.