Sept 16, 1997
Some gyrofluid R/L_T_crit issues are discussed below, to clarify when I use the "thesis closure" and when I use the "marginal stability" closure, and how they are different. All my official cyclone runs except some early linear runs have used the "thesis closure" and are far enough from marginal stability that the topic discussed below is not a serious issue. I'm proposing that the R/L_T_crit in Scott's table should be changed to "4.0 (extrapolated)". If this paragraph doesn't interest you, read no further, the rest is a bit long-winded. A brief discussion on this topic is in Sec. VI of Beer & Hammett, PoP 3, 4046 (1996).
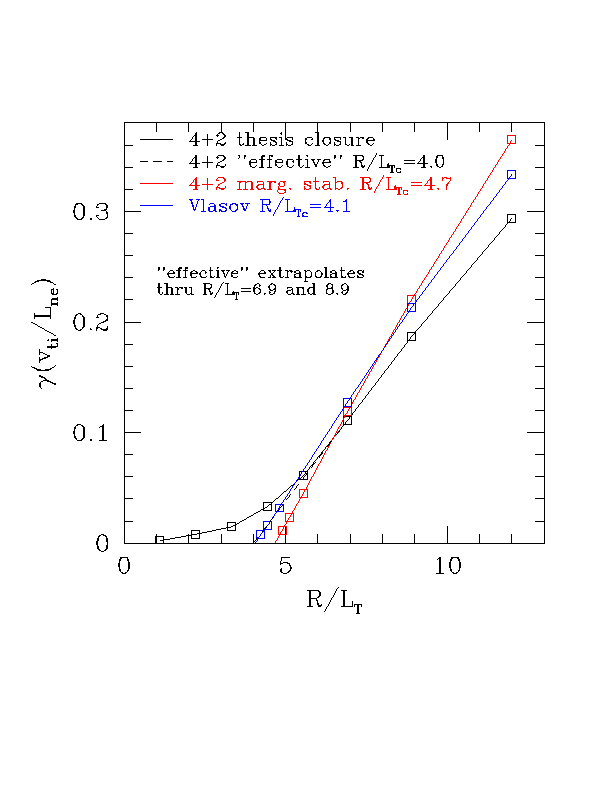
All the discussion below is in the adiabatic electron, circular, T_i=T_e, and no impurities limit. In the figure below all parameters are 81499 base case varying R/L_T only.
When I originally found the 4+2 toroidal closure coefficients in my thesis, I was concentrating on matching linear kinetic theory for growing modes, and was not too concerned about the fit very near marginal stability. I found a good fit to the response function over the upper-half omega plane. There are small errors in this gyrofluid response function, and near marginal stability these errors produce a spurious weakly growing mode. These linear growth rates are shown as the black curve in the figure below, and there is a weak spurious instability for R/L_T<4. Thus for the "thesis closure" R/L_T is way off, but below the real R/L_T_crit, the growth rate is weak. Away from marginal stability, these errors are swamped by parts of the real response function which become large.
Later, to have more accurate behavior near threshold, I found another set of closure coefficients which gives a reasonable fit to the response function over the upper-half omega plane, and, made sure that the small errors cancelled on the real axis to give a good linear threshold. In the upper-half plane, the fit from this "marginal stability" closure is not generally as good as the original "thesis closure". The growth rates from this marginal stability closure are shown in red below, and give R/L_T_crit=4.7, and much better behavior near threshold. This value of R/L_T_crit=4.7 is what I originally reported in Scott's table.
For comparison, the growth rates from Peter Liu's gyrokinetic Vlasov code are in blue, and give R/L_T_crit=4.1.
To deal with this problem near marginal stability, when I run for a new set of parameters, I first run linearly with the marginal stability closure to see if there is an instability. If there is, I then run with the thesis closure to get more accurate growth rates, unless it's really close to marginal stability.
I've defined an "effective" R/L_T_crit for the thesis closure by linearly extrapolating the growth rate through the base case (R/L_T=6.9), shown by the black dashed line in the figure. This extrapolates to an "effective" R/L_T_crit of 4.0, and also fits the +-30% points very well. (The -30% R/L_T point is still above where the spurious instability is appreciable.) So I guess the gyrofluid R/L_T_crit in the table should be changed to "4.0 (extrapolated)".
This issue is why the IFS-PPPL model uses a kinetically calculated R/L_T_crit.
--Mike.

Back to index of cyclone pages
Back to Mike Beer's home page