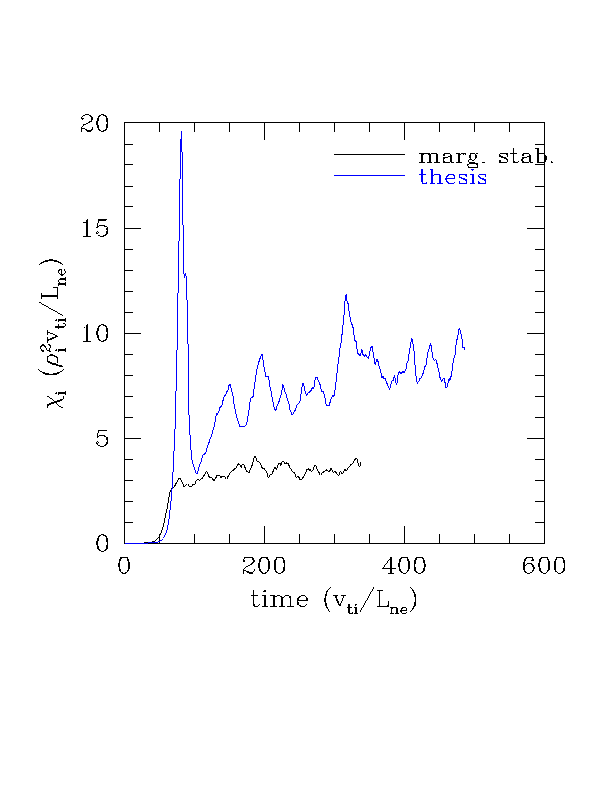
Here are a few results related to the gyrofluid errors near marginal stability (MS) and the effects of using the "thesis closure" or the "MS closure". To summarize the results, it seems to us that the agreement between the MS closure and the GK results for the base case is somewhat accidental, because the MS closure has significantly lower growth rates at long wavelengths for the base case, so that one would naturally expect a lower chi.
1. Below are GF nonlinear runs using the thesis closure and the MS closure. The MS closure chi is much closer to the GK chi.

2. However, the apparent agreement between the MS GF run and GK seems accidental, because the MS growth rates are very low at the important long wavelengths. This is shown in the linear comparison below. The thesis linear growth rates are very accurate (open circles, black), while the MS closure linear growth rates are way off at low k-theta (open circles, red). (Compare to kinetic results, dashed line.)
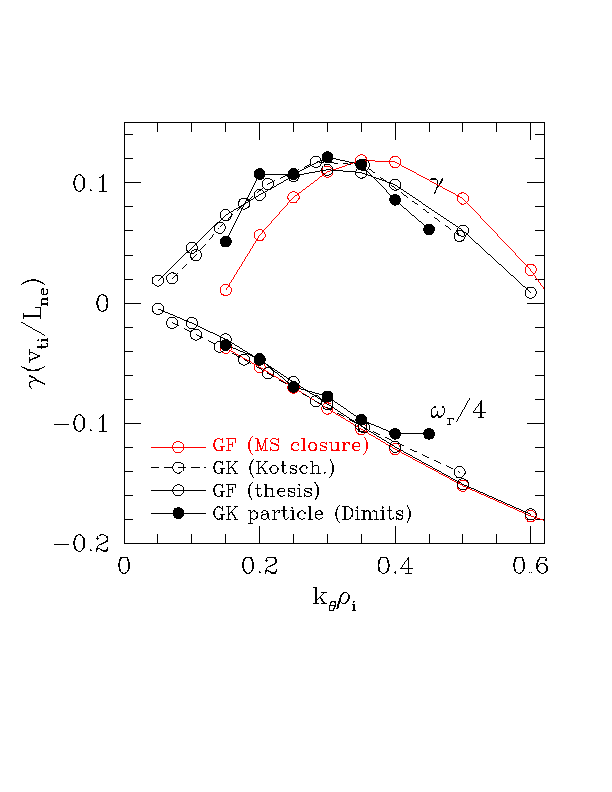
Conclusion: Since the MS closure is only accurate near threshold, away from threshold the thesis closure should be used. The thesis linear growth rates are very accurate for the base case, while the MS linear growth rates are way off. For the base case, the nonlinear chi from the MS closure is lower because of these low linear growth rates. The apparent agreement with GK seems accidental.
The linear gyrofluid errors near threshold (using the thesis closure) go away as one moves above threshold. This is evident from the linear theory plot above (and is discussed more here). The MS closure gains accuracy near threshold at the expense of accuracy above threshold. We do not trust a nonlinear result when the linear theory is too far off, which is why we do not use the MS closure far from marginal stability.
It seems to us that this is all consistent with gamma/k_perp^2 expectations. The MS closure lowers the growth rate at long wavelengths, so one would expect the peak in gamma/k_perp^2 to shift to higher k_theta. In the nonlinear run, the spectrum indeed shifted upwards in k_theta by about a factor of 2, and one would expect the chi to drop by about a factor of 2, as it did. Our original motivation for making this plot was to show that chi can be fairly sensitive to the long wavelength growth rate spectrum. The linear growth rates from Andris's code look fairly good over the range plotted, but we think it would be useful to also plot the growth rates at k_theta rho_i=0.1 and 0.05 just to make sure everything is okay down there.
We have always acknowledged that the GF equations had some difficulties near marginal stability, which is why the nonlinear GF results were scaled by linear GK stability codes to get a more accurate threshold for the IFS-PPPL model. Some of the difficulties of the gyrofluid closures near marginal stability were first noted and discussed in Waltz, Dominguez and Hammett, Phys. Fluids B4, 3138 (1992). See the discussion in Sec. II or the conclusions. They felt that this small residual instability below the kinetic critical gradient was somewhat exaggerated in the adiabatic electron limit, and that the situation improved with nonadiabatic electrons, though they also suggested some other ways to perhaps improve the closure further.
--Mike
Back to index of cyclone pages
Back to Mike Beer's home page