Here is a brief description of my research interests and projects: My main fields of research are accelerator physics, physics and chemistry of plasmas and fluids, nonlinear transport phenomena and stochastic processes, atomic physics. I have broad experience in various areas of accelerator and plasma physics, which includes but not limited to: · high-energy density physics (HEDP)
· low-temperature plasmas and gas-discharge physics
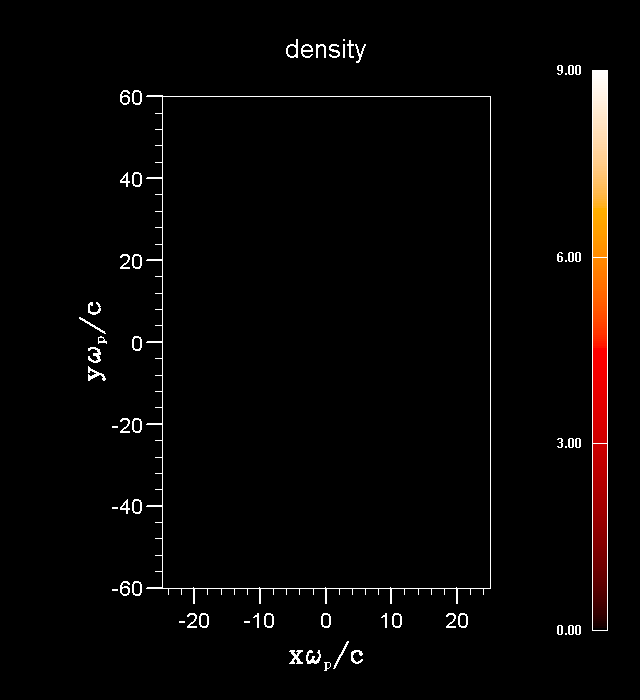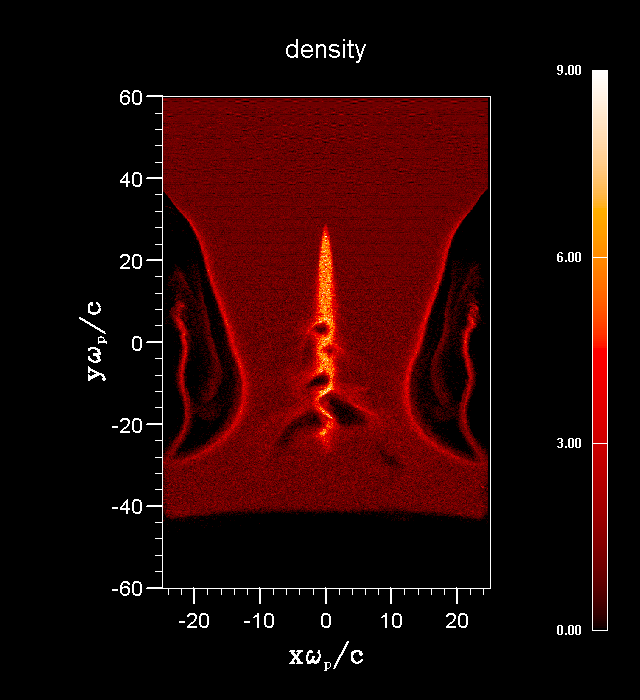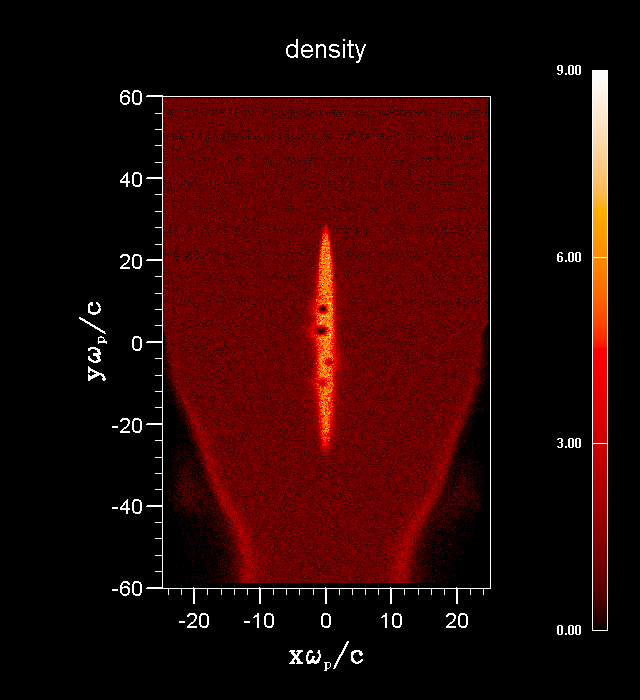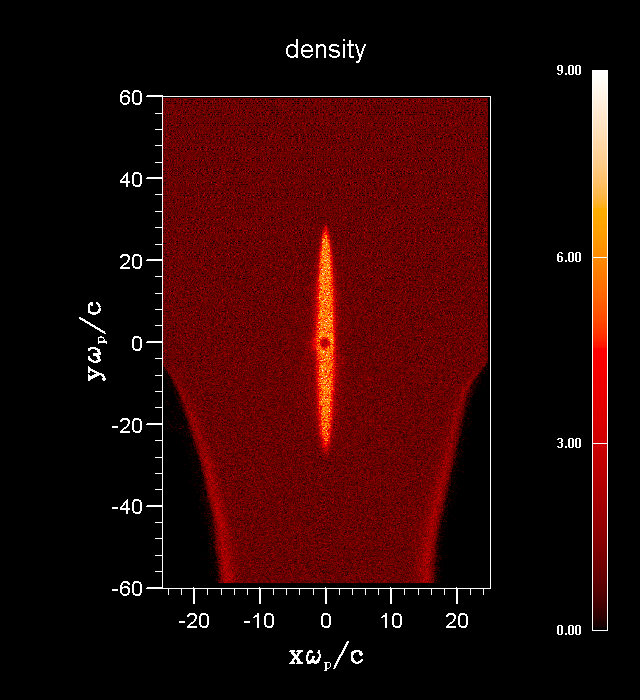
High-energy density plasma physics Ion beam-plasma interaction The charge and current neutralization of an ion beam propagating in a preformed plasma have been studied. Application of the conservation law of generalized vorticity and making use of a small parameter - ratio of the beam radius to the beam length allowed reducing system of equations and developing robust computational tool for simulation of beam plasma interaction. To check the theoretical predictions and benchmark particle-in-cell code, a two-dimensional electromagnetic fluid code was developed, which can predicts in few minutes, whereas full scale particle-in-cell code requires much longer computational times and resources. Movies generated from the code results show complex phenomena occurring during beam entry into plasma and exit from plasma. Atomic physics for HEDP applications The second example pertains to study of multiple electron stripping of heavy ion beams. Heavy ion beams lose electrons while passing through background gas in the target chamber, and therefore it is necessary to assess the rate at which the charge state of the incident beam evolves on the way to the target. Accelerators designed primarily for nuclear physics or high-energy physics experiments utilize ion sources that generate highly stripped ions in order to achieve high energies economically. As a result, accelerators capable of producing heavy ion beams of 10 to 40 Mev/amu with charge state 1 currently do not exist. Hence, the stripping cross-sections used to model the performance of heavy ion fusion driver beams have, up to now, been based upon theoretical calculations. The cross sections are calculated using different techniques. The Born approximation, which results in overestimate of the cross sections, should be valid for Ze2<<hV, where Z is the target atomic number and V is the velocity of the beam ion relative to the target atom. The classical trajectory calculations do not account for tunneling transitions allowed by quantum mechanics. Neither approach is expected to perform well across a wide spectrum of beams and targets. Aspects of one approach must be combined with parts of the other approach in order to address shortcomings in the underlying assumptions. This was accomplished by using matching of different techniques in their range of validity. The resulting theoretical values for cross sections agree well with experimental data. Collective effects and turbulence The plasma is subject of numerous instabilities. For many applications it is important to access rate of instabilities and nonlinear stage of saturation and corresponding anomalous transport. For low-pressure discharges most instabilities are associated with particle production, mostly due to nonlinear dependence of ionization frequency on electric field. The instability lead to complicated two-three dimensional structure of discharges. Few examples for dc and rf discharges have been studied. For HEDP applications instability mainly occurs due to motion of particle beams relative to background plasma. Intense beam propagating in plasma drive various plasma instabilities: two-stream, Weibel's, Buneman's, etc.. The nonlinear stage of instabilities, saturation and corresponding wave-turbulence is important and part of studies of HEDP plasmas.
Low-temperature plasmas and gas-discharge physics Kinetic effects and studies of non-Maxwellian electron energy distribution functions The modern trend in plasma technology aims at decreasing gas pressures down to mTorr range. At these low pressures, it is easier to maintain uniform plasmas with well-controlled parameters. In low-pressure plasmas the electron mean free path can be larger or comparable to the plasma characteristic inhomogeneity scale. Therefore, the electron transport is collisionless and nonlocal, since an electron can traverse a significant distance between collisions and sample different values of electric field along its way. As a result, the electron current is determined not by the local electric field, but by the entire profile of the electric field. Also for inhomogeneous electric fields another mechanism of heating or power dissipation is possible, which is strikingly different from collisional one; namely collisionless heating is determined by the wave-particle resonances and independent of the collision frequency. Moreover, the electrons are frequently not in equilibrium with themselves, and as a result, the electron energy distribution functions in such plasmas are typically non-Maxwellian. This property makes plasmas a remarkable tool for plasma applications, including plasma processing, lighting, plasma sources, thrusters, etc. Collisionless heating and anomalous phenomena in plasmas Due to the large value of mean free path, the main mechanism of electron heating turns out to be a collisionless heating rather than conventional Ohmic heating, which is dominant for higher pressures. Therefore, a quantitative description has to be developed for collisionless heating in nonuniform plasmas of low-pressure discharges. The role of collisions and non-linear effects was investigated; it was shown that collisions play an important role even in collisionless heating as a decorrelation process. Under certain conditions, collisionless heating is proportional to collision frequency due to the influence of nonlinear effects. This is in contrast to the common situation, where collisionless heating does not depend on collision frequency, as in the classical theory of Landau damping and anomalous skin effect. Based on quasi-linear theory, a self-consistent treatment of collisionless heating was performed for various types of low-pressure discharges and thrusters. This system includes the kinetic equation for the electron distribution function in self-consistent electric field. Straightforward numerical modeling of such system is quite complicated. An effective semi-analytical method of solving this system was developed. The principles of fast modeling of low-pressure discharges are based on averaging over fast electron and ion motions and eliminating a small spatial scale, the Debye radius. As a result, the solution of a self-consistent system of the electron kinetic equation, the Poisson equation, and the ion continuity equation is approximately hundreds times faster compared with straightforward numerical techniques. Transport in multi-component plasmasTransport in multi-component plasma is very different from a transport of plasma comprising from only electrons and ions. In particularly, the multi-component plasma tend to stratify into region of different composition, completely opposite to the naive first assumption. The negative ion fronts of sharp gradient of negative ion density was shown to to form during all stages of plasma evolution: ignition, steady-state and afterglow. Transport in magnetized plasmasThe ambipolarity condition for electron and ion transport in magnetized plasma in two dimensions causes rather complicated flow patterns. Electrons can flow fast along the magnetic field lines and simultaneously diffuse radially far then come back along another magnetic field lines. As a result, ions can flow freely to the radial position where electrons are available due to such complex loop-like electron trajectories. An example of such transport is plasma jet's radial expansion in presence of strong axial magnetic field. The "conventional wisdom" approach predicts a conical shape for the plasma jet. This stems from the assumption that electrons and ions diffuse together across the magnetic field lines with an effective ambipolar diffusion coefficient taking from one-dimensional theory. However, such "conventional wisdom" approach fails in two-dimensional geometry, because electrons and ions trajectories are very different in 2D. The short-circuiting electron flows result in a cylindrical shape of the jet in contrast to conical. |
Research Interests |