Model with width based on magnetic and flow shear stabilization

  This model is given by Eq. (13) in Ref. [5]. It was assumed in this model that the pressure gradient within the pedestal region is constant and limited by the first stability of the ballooning mode. Then, the total pressure at the top of the pedestal () is
 
where and are the density and temperature at the top of the pedestal, k is the Boltzmann's constant, is the pedestal width and is the critical pressure gradient of ballooning mode. Rewriting Eq. (), one can obtain the value of ,
 
given the value of the pressure gradient and the width of the pedestal region.

In this model, the width of the pedestal, , is assumed to be determined by a combination of magnetic and flow shear stabilization of drift modes [4],
 
where s is the magnetic shear, is the ion gyro-radius at the inner edge of the steep gradient region of the pedestal and C_W is a constant of proportionality chosen to optimize the agreement with experimental data. The first stability ballooning mode limit is approximated by
 
where the magnetic q and shear s are evaluated one pedestal width away from the separatrix, R is the major radius, B_T is the vacuum toroidal magnetic field evaluated at major radius R, is the elongation at the 95% magnetic surface (, where is the elongation at the separatrix) and is the triangulrity at the 95% magnetic surface (, where is the triangularity at the separatrix).

After combining Eqs. ,  and  with some algebra, the following expression can be obtained for the pedestal temperature [5]:
 
where is the pedestal temperature in the unit of keV, A_H is the average hydrogenic ion mass in the unit of AMU and is the electron density at the top of the pedestal in units of m³.

The magnetic q has a logarithmic singularity at the separatrix. At one pedestal width away from the separatrix, the magnetic q is approximated by
 
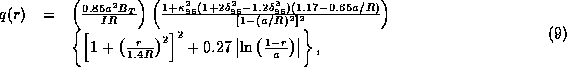
where is the position of the top of the pedestal and I is the plasma current. The magnetic shear, , which is computed using the magnetic q from Eq. (), is then reduced by the effect of the bootstrap current, as described in Ref. [5]. Since the pedestal width is needed to compute the magnetic q , the magnetic shear, s , and the normalized pressure gradient , and since the pedestal width is a function of the pedestal temperature, the right hand side of Eq. () for the pedestal temperature depends nonlinearly on the pedestal temperature. Consequently, a non-linear equation solver is required to solve Eq. () to determine .

The coefficient C_W in the expressions for the pedestal width [Eq. ()] and the pedestal temperature [Eq. ()] is determined by calibrating the model for the pedestal temperature against 533 data points for type I ELMy H-mode plasmas obtained from the International Pedestal Database version 3.1, using discharges from ASDEX-U, DIII-D, JET, and JT-60U tokamaks, as described in Ref. [5]. Ion temperature measurements were used for the pedestal temperature whenever they were available. However, this pedestal temperature model does not distinguish between electron and ion temperature. It is found that the value C_W = 2.42 yields a minimum logarithmic RMS deviation of about 32.0% for this data.