Angular Momentum
From QED
In classical mechanics the angular momentum of a single particle about a given point r' is given by
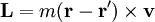
For a system of particles or a continuous object, it is given by
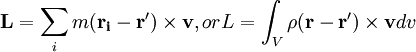
In a potential field that is rotationally invariant about a point, the angular momentum of a single particle about that point is always conserved. This holds true for a system of particles or a continuous object by linearity. Note, however, that the angular momentum about other points, (say, the center of mass of the object) is not always conserved. See gravitational stabilization for example
The angular momentum about an object's center of mass of an object rotating about some point is simply
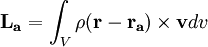
Compare this to the angular momentum about any other point of the same motion:
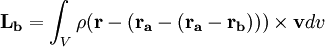
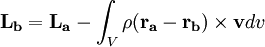
Consider each axis in the remaining integral. The magnitude along these axes is
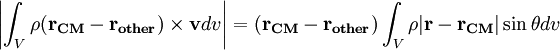
Since the distribution of mass about the center of mass is by definition balanced, the final integral vanishes, and
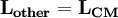
Here we see that the angular momentum about any axis, of an object rotating about it's center of mass is invariant. Thus a system of objects rotating in this manner may simply have their angular momentums added in an arithmetical fashion.
The center of mass is special. Commonly, the motion of an object is described by the translational velocity of the object 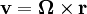 ).
).
Given an inertia tensor I, the angular momentum about the center of mass is given by
As is the general pattern in such things, replacing velocity by linear momentum and the cross product by a wedge product yields the relativistic definition
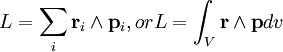
This page was recovered in October 2009 from the Plasmagicians page on Angular_Momentum dated 00:48, 30 March 2007.












