Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

Billiards

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/Billiards]])

Jump to: navigation, search

We make the following assumptions. The essence of the problem is retained while adding these. We do not consider the consider the general case because it obscures the argument (we could 'prove it' through simulation, but you wouldn't get the insight).

- Elastic Collisions
Spherical Collisions
Neglect 3 or higher body collisions
Frictionless Surface

We are to show that a small perturbation in the positions of balls is amplified exponentially by a factor proportional to the length of the table.

Note: The argument may be adapted to the case of bouncing a ball against a curved surface, such as shown here: http://wims.unice.fr/wims/wims.cgi?lang=en&+module=H6%2Fgeometry%2Fellbillard.en

We treat the table like it has periodic boundary conditions (this is nearly correct)

Rotate the system, during each collision, to the same vertical frame of reference where the upper ball (denoted $u$ ) travels downward, and the lower ball (denoted $l$ ) travels upward. Adopt the inertial frame where the lower ball is standing still before the collision.

In this frame, the energy and momentum of the system are

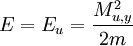
$E = E_{u} = \frac{M_{u, y}^2}{2m}$

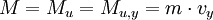
$M = M_{u} = M_{u, y} = m \cdot v_y$

The force felt during the collision is directed along the angle $α$ from the center of the lower ball to the second. This may be specified by the impact parameter, $b$ , the horizontal difference between the centers of each of the balls.

The lower ball moves along no other trajectory. Thus it's momentum, post collision, is proportional to the following:

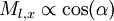
$M_{l,x} \propto \cos(\alpha)$

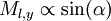
$M_{l,y} \propto \sin(\alpha)$

And 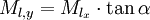$M_{l,y} = M_{l_x} \cdot \tan{\alpha}$ .

We put all the momenta in the form of a single parameter, then use energy conservation to deduce that parameter.

Since horizontal momentum is conserved

$M l, x = - M u, x$

Since vertical momentum is conserved

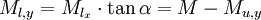
$M_{l,y} = M_{l_x} \cdot \tan{\alpha} = M - M_{u,y}$

or 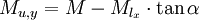$M_{u,y} = M - M_{l_x} \cdot \tan{\alpha}$

Thus the total energy is

$\frac{1}{2m} \left[{M_{l,x}^2 + M_{u,x}^2 + M_{l,y}^2 + M_{u,y}^2}\right]$

$E = \frac{1}{2m} \left[{M_{l,x}^2 + M_{l,x}^2 + M_{l_x}^2 \cdot \tan^2{\alpha} + (M - M_{l_x} \cdot \tan{\alpha})^2 }\right]$

Solving for $M l, x$

$0 = \left[{2 M_{l,x}^2 (1 + \tan^2{\alpha}) - 2 M_{l,x} M \tan{\alpha} + M^2 - 2mE}\right]$

$0 = \left[{2 M_{l,x}^2 (1 + \tan^2{\alpha}) - 2 M_{l,x} M \tan{\alpha}}\right]$

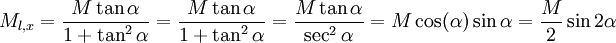
$M_{l,x} = \frac{M \tan{\alpha}}{1 + \tan^2{\alpha}} = \frac{M \tan{\alpha}}{1 + \tan^2{\alpha}} = \frac{M \tan{\alpha}}{\sec^2{\alpha}} = M \cos(\alpha) \sin{\alpha} = \frac{M}{2} \sin{2 \alpha}$

For small angular displacements 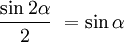$\frac{\sin{2 \alpha}}{2} ~= \sin{\alpha}$ (and this approximation remains valid for a sizable proportion of the collisions).

We use the fact that 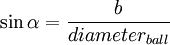$\sin{\alpha} = \frac{b}{diameter_{ball}}$ (while b is less than the diameter of the ball).

Or, in units of ball diameters, $sinα = b$

Thus 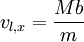$v_{l,x} = \frac{M b}{m}$ -- linear with respect to the displacement.

Now, the distance that the lower ball will move along the x axis until the next collision will be approximately 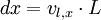$dx = v_{l,x} \cdot L$ , where $L$ is the length scale of the table (luckily billiards has periodic boundary conditions!).

Suppose $b$ is altered by some small amount, $δ b$ . Then the distance along x that the lower ball will be displaced will be roughly $\delta x = \left[{\frac{M \delta b}{m}}\right] \cdot T$ , where $T$ is the average time between collisions.

The next collision will then have a different impact parameter that's different by $δ x$ .

Repeat this process over $n$ bounces. The displacement from the ball's original path will be

$\delta x (n) = \left[{\frac{M \delta x (n - 1) T }{m}}\right]$

or $\delta x (n) = b \left[{\frac{M T}{m}}\right]^n$ .

$M T = m σ$ where $σ$ is the mean free path of a ball (obviously larger than the diameter of one ball), thus

$δ x (n) = b σ n$ .

This shows that the size of the horizontal displacement is amplified exponentially, and thus billards is chaotic.

- Billiard Ball diameter: 2.25" in = 0.05715 m (I'll call this unit 1 ball)
Billiard Ball weight: 5.5 oz = 0.155922377 kg
Billiards length scale: ~9feet = 48 balls ~= 3 meters
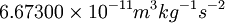
G = $6.67300 \times 10^{-11} m^3 kg^{-1} s^{-2}$

A 100 kg friend is standing 10 meters away from the table. The mean free path is, I will guess, ~3 meters.

After a ball travels 3 meters at about 3 meters per second (1 second), it is displaced by the graviational force of your friend by

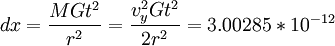$dx = \frac{M G t^2}{r^2} = \frac{v_y^2 G t^2}{2 r^2} = 3.00285 * 10^{-12}$ .

Or 3 nanometers. In ball units, $b = 5.25 * 10 - 8$ . How long would it take for balls that would bounce straight against each other indefinitely to miss entirely due to your friend?

Solving $1 = δ x (n) = b σ n$ for n:

$0 = log b σ n = log b + logσ n$

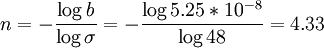$n = -\frac{\log{b}}{\log{\sigma}} = -\frac{\log{5.25 * 10^{-8}}}{\log{48}} = 4.33$ ,