Boltzmann distribution

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/Boltzmann distribution]])
Jump to: navigation, search

For a closed macroscopic system of quasi-classical particles (where some of the degrees of freedom behave classically, while the other degrees of freedom are quantised), the distribution function is given by the Gibbs Distribution

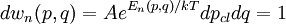
dw_{n}(p,q)=Ae^{E_{n}(p,q)/kT}dp_{cl}dq=1

Here, the quantum numbers n represent the quantized components of motion, and pcl is the differential representing the classical momenta.

In the classical form of the Gibbs distribution

dw(p,q) = AeE(p,q) / kTdpcldq = 1

We may write the energy function as a sum of the kinetic energy (a function of momentum) and potential energy (a function of position) becomes E(p,q) = K(p) + U(q). This, neglects, of course, the vector potential because it does not contribute to the energy of the particles. We may then seperate the distribution function

dw(p,q) = ∏dwp,i(pi)dwq,i(qi)
iε{dimensions}
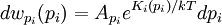
dw_{p_{i}}(p_{i})=A_{p_{i}}e^{K_{i}(p_{i})/kT}dp_{i}
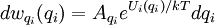
dw_{q_{i}}(q_{i})=A_{q_{i}}e^{U_{i}(q_{i})/kT}dq_{i}

We now have

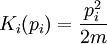
K_{i}(p_{i})=\frac{p_{i}^{2}}{2m}

In the absence of magnetic fields (or other fields inducing velocity dependent forces), and neglecting relativity

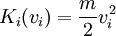
K_{i}(v_{i})=\frac{m}{2}v_{i}^{2}

Normalizing our probabilities

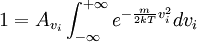
1=A_{v_{i}}\int_{-\infty}^{+\infty}e^{-\frac{m}{2kT}v_{i}^{2}}dv_{i}

Using the formula for a Gaussian integral

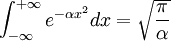
\int_{-\infty}^{+\infty}e^{-\alpha x^{2}}dx=\sqrt{\frac{\pi}{\alpha}}
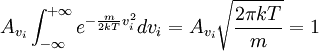
A_{v_{i}}\int_{-\infty}^{+\infty}e^{-\frac{m}{2kT}v_{i}^{2}}dv_{i}=A_{v_{i}}\sqrt{\frac{2\pi kT}{m}}=1
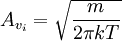
A_{v_{i}}=\sqrt{\frac{m}{2\pi kT}}

Giving us

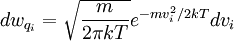
dw_{q_{i}}=\sqrt{\frac{m}{2\pi kT}}e^{-mv_{i}^{2}/2kT}dv_{i}

This is the so-called one dimensional Maxwell-Boltzmann distribution. In d-dimensions

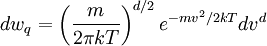
dw_{q}=\left(\frac{m}{2\pi kT}\right)^{d/2}e^{-mv^{2}/2kT}dv^{d}

Where d = 3 is the most familiar solution

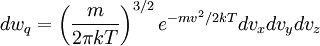
dw_{q}=\left(\frac{m}{2\pi kT}\right)^{3/2}e^{-mv^{2}/2kT}dv_{x}dv_{y}dv_{z}

It should be noted that while in a system with less than two spatial degrees of freedom the maximum entropy distribution is indeed Maxwellian, a system which is not in a Maxwellian state will not relax to one because collisions can only swap momenta. Thus in the limit where the magnetic field approaches infinity the system approaches one dimensionality and the thermal relaxation time approaches infinity.

This page was recovered in October 2009 from the Plasmagicians page on Maxwell-Boltzmann_distribution dated 23:10, 25 October 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Boltzmann_distribution"
Personal tools