Differentiation of Inverse Functions

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/Differentiation of Inverse Functions]])
Jump to: navigation, search

Knowing this theorem is useful in many ways. It is, in fact, a source of obscure tricks, but it also gives a succinct and effective method for remembering strange derivatives like those of inverse trigonometric functions, the kinds which we encounter so incredibly often in physics. Remembering those derivatives is now reduced to remembering a few core trigonometric identities, and the derivatives of the basic trigonometric functions.

Let f(x) be a function which is differentiable on the open interval I.

If 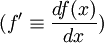(f' \equiv \frac{df(x)}{dx}) for all x in I then f has an inverse f − 1 which is defined and is differentiable on f(I). That is, for each a in I, f − 1 is differentiable at b = f(a) and

\frac{d}{db} f^{-1}(b) = \left[{\frac{d f(a)}{da}}\right]^{-1}

First, we remark that f − 1 is defined, as f is bijective over I. Next, we remark that since f is differentiable, so is f − 1 which may be shown simply by swapping the axes of the f(x) graph.

First, parameterizing a = a(t),b = b(t).

Now, starting from the definition of b,b = f(a), we must have a = f − 1(b). Then

\frac{da}{dt} = \frac{d}{dt} \left[{f^{-1}(b)}\right] = \frac{d}{db} \left[{f^{-1}(b)}\right] \frac{db}{dt}

Recalling that b = f(a),

\frac{d}{db} \left[{f^{-1}(b)}\right] \frac{db}{dt} = \frac{d}{db} \left[{f^{-1}(b)}\right] \frac{d f(a)}{dt} = \frac{d}{db} \left[{f^{-1}(b)}\right] \frac{d f(a)}{da} \frac{da}{dt}

Or

\frac{da}{dt} = \frac{d}{db} \left[{f^{-1}(b)}\right] \frac{d f(a)}{da} \frac{da}{dt}

Cancelling 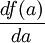\frac{d f(a)}{da} which by assumption is non-zero, we arrive at our desired result:

\frac{d}{db} f^{-1}(b) = \left[{\frac{d f(a)}{da}}\right]^{-1}

As alluded to above, this takes some of the mystery out of those inverse trigonometric derivatives. For example,

Let y = sinφ. Then

\frac{d \arcsin{y}}{d y} = \left[{\frac{d \sin{\phi}}{d\phi}}\right]^{-1}
\frac{d \arcsin{y}}{d y} = \left[{\cos{\phi}}\right]^{-1}

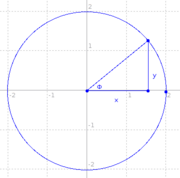
Referring to our highschool triangle diagram, we see that

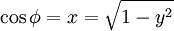
\cos{\phi} = x = \sqrt{1 - y^2}

Hence, as our first-year calculus teachers asserted,

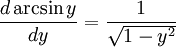
\frac{d \arcsin{y}}{d y} = \frac{1}{\sqrt{1 - y^2}}

Remarkably, the other formulas are similarily derivable. Think of the wasted time you spent fumbling around in the dark for your integral tables! Fumble no more!

This page was recovered in October 2009 from the Plasmagicians page on Differentiation_of_Inverse_Functions dated 20:44, 26 November 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Differentiation_of_Inverse_Functions"
Personal tools