Ehrenfest's Theorem
From QED
If 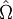 is an operator with no explicit time dependence, then
is an operator with no explicit time dependence, then
![\frac{d}{dt} \langle \hat{\Omega} \rangle = \left({\frac{-i}{\hbar}}\right) \langle \phi | [\hat{\Omega}, \hat{H}] | \phi \rangle + \langle \phi | \hat{\dot{\Omega}} | \phi \rangle](../../images/math/9/a/1/9a10a482599302f99aa390887995c68f.png)
Ehrenfest's Theorem describes the time evolution of the expected value of dynamic variables. The relations that derive from this system share a striking similarity to the relations of classical physics. For the majority of systems, as the size of the system increases the relative fluctuations decrease, and so the systems begin to resemble, more and more, their classical counterparts.
By the product rule
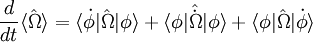
By the Schrödinger Equation
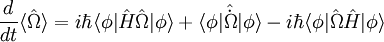
Finally
![\frac{d}{dt} \langle \hat{\Omega} \rangle = \left({\frac{-i}{\hbar}}\right) \langle \phi | [\hat{\Omega}, \hat{H}] | \phi \rangle \langle \phi | \hat{\dot{\Omega}} | \phi \rangle](../../images/math/5/2/e/52e8fe22703ab9c5444733d359ae1a8f.png)
Note the striking similarity to the classical equation, written in terms of Poisson Brackets.
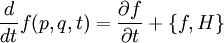
This page was recovered in October 2009 from the Plasmagicians page on Ehrenfest's_Theorem dated 19:53, 6 December 2006.












