Electromagnetic waves (dispersion)
From QED
A plasma acts as a dielectric medium for electromagnetic waves. Waves with frequencies slow compared to the plasma frequency will be significantly damped. This is described by the dispersion relation :
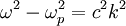
This is a valid relation for homogenous unmagnetized cold plasmas.
We start off with some of Maxwell's equations :
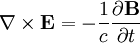
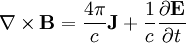
And the vector relation :
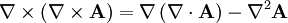
Taking the cross product of the first relation and using the vector identity:
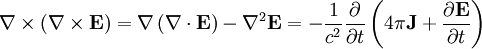
We can rewrite the current as:
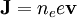
And writing the Lorentz force equation
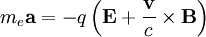
Since v1 is a perturbed quantitiy and v0 = 0, we can assume it is small compared to c and neglect the magnetic contribution to the lorentz force:
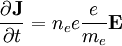
so that:
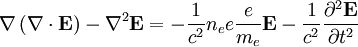
We can write the perturbed values in terms of plane
waves moving in the  direction, for example:
direction, for example:
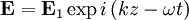
Here we have taken E0 = 0 (no zero order electric field). Plugging in:
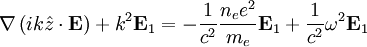
The first term on the left must be zero, since the electric field must be perpendicular to the wave vector:
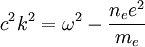
Using the plasma frequency 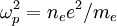 , we get the dispersion relation:
, we get the dispersion relation:
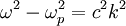
This page was recovered in October 2009 from the Plasmagicians page on Electromagnetic_waves_(dispersion) dated 22:38, 10 April 2007.












