Energy
From QED
Energy. It's a big deal. Nature didn't have to actually conserve anything, but incredibly, she does, and quite effectively, too. You may even state (in fact, the First Law of Thermodynamics does) that she's perfect at it. She doesn't have to be. But for every single system we've ever observed, energy is conserved.
In more radically constrained systems, like considered in, we can actually start talking about the type of energy. Let's do that.
Taking the derivative of the Lagrangian with respect to time, and assuming that the Lagrangian is not an explict function of time.
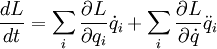
Applying the product rule (backwards)
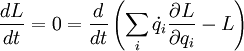
Evidently,
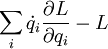
is constant with respect to time. It's called energy.
In a constant field, 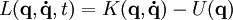 (where K is known as the kinetic energy, and U is the potential energy), and (knowing that K is a quadratic homogenous function on v*)
(where K is known as the kinetic energy, and U is the potential energy), and (knowing that K is a quadratic homogenous function on v*)
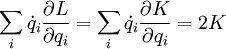
giving the familiar form
This page was recovered in October 2009 from the Plasmagicians page on Energy dated 18:50, 30 March 2007.












