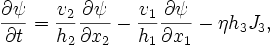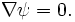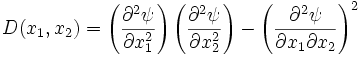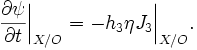Flux Surfaces and Magnetic Islands
From QED
Many plasma configurations are strongly anisotropic because of the presence of a preferentially-directed magnetic field. If the system has a direction of symmetry, such as toroidal symmetry in tokamaks, then analysis of the system can be greatly simplified by the introduction of a magnetic flux function 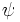 . The flux function is chosen such that the magnetic field
. The flux function is chosen such that the magnetic field 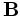 lies on surfaces of constant
lies on surfaces of constant 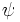 , called flux surfaces. This is mathematically stated by the condition that
, called flux surfaces. This is mathematically stated by the condition that
In the plane perpendicular to the direction of symmetry in the system, the magnetic fieldlines are simply contours of constant 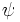 .
.
Contents |
General Flux Function Form of the Magnetic Field
Examine the system in a generalized curvilinear coordinate system defined by the coordinates 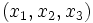 . The differential displacement vector in such a coordinate system is given by
. The differential displacement vector in such a coordinate system is given by
where the geometric factors 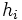 are related to the Cartesian coordinates
are related to the Cartesian coordinates 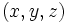 by
by
Working in these generalized coordinates, if 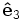 is taken to be the direction of symmetry, then the magnetic field can be written in the form
is taken to be the direction of symmetry, then the magnetic field can be written in the form
where 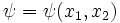 and
and 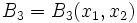 . This form of
. This form of 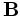 trivially satisfies
trivially satisfies 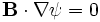 , and the factor of
, and the factor of 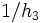 ensures that
ensures that 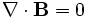 .
.
In Cartesian 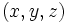 coordinates with
coordinates with 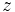 -directed symmetry,
-directed symmetry, 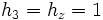 , giving
, giving
In cylindrical 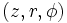 coordinates with
coordinates with 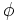 -directed symmetry,
-directed symmetry, 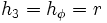 , so
, so
The 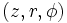 ordering is chosen so that the coordinate system is still right handed when
ordering is chosen so that the coordinate system is still right handed when 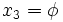 .
.
Relation Between the Flux Function and the Magnetic Vector Potential
The flux function 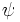 can be related to the magnetic vector potential
can be related to the magnetic vector potential 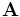 , which is given by
, which is given by
Expanding the curl operator in the aforementioned generalized curvilinear coordinates, the above equation becomes
Because symmetry is assumed along 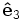 and thus
and thus 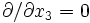 , the expression for
, the expression for  becomes
becomes
Now expand the flux-function form of 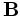 in a similar manner. Begin with
in a similar manner. Begin with
Substituting the above expression into the flux-function form of 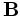 gives
gives
Subtracting the flux-function form of 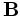 from the vector potential form leaves
from the vector potential form leaves
From the above equation, it is clear that, to within a constant,
Consequently, in Cartesian 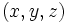 coordinates,
coordinates, 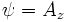 , and in cylindrical
, and in cylindrical 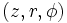 coordinates,
coordinates, 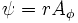 .
.
Time Evolution of the Flux Function in Resistive MHD
Assuming that, as in MHD, the scalar electrostatic potential 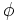 is negligible due to quasineutrality, Faraday's Law gives the electric field to be
is negligible due to quasineutrality, Faraday's Law gives the electric field to be
Substituting for 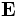 using the generalized Ohm's Law from resistive MHD (
using the generalized Ohm's Law from resistive MHD (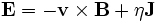 ) gives
) gives
From above, 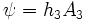 , so to find
, so to find 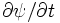 , examine the
, examine the 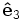 component of the above equation:
component of the above equation:
where the flux function form of 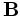 has been used. The final form for
has been used. The final form for 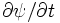 is then
is then
Topological Properties of the Flux Function: X-Points, O-Points, and Magnetic Islands
The flux function 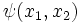 can exhibit many of the topological characteristics associated with multi-dimensional functions such as maxima, minima, and saddle points. Maxima and minima in the flux function are called O-points, and saddle points are called X-points. Magnetic fieldlines are contours of constant
can exhibit many of the topological characteristics associated with multi-dimensional functions such as maxima, minima, and saddle points. Maxima and minima in the flux function are called O-points, and saddle points are called X-points. Magnetic fieldlines are contours of constant  in the
in the  plane, so the X- and O-point designations arise because a fieldline forms an "X" shape when passing through and X-point and an "O"-shaped ring when circling an O-point.
plane, so the X- and O-point designations arise because a fieldline forms an "X" shape when passing through and X-point and an "O"-shaped ring when circling an O-point.
The mathematical condition for the existence of an X- or O-point is that
To distinguish between extrema (minima or maxima) and saddle points, use the multi-dimensional second derivative test. Construct the quantity 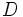 , which has the form
, which has the form
Not sure if this form of 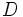 is valid for any arbitrary curvilinear coordinate system. The
is valid for any arbitrary curvilinear coordinate system. The 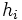 factors could play a non-negligible role in above the expression. Regardless, examining
factors could play a non-negligible role in above the expression. Regardless, examining 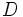 at the point
at the point 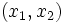 distinguishes X- and O-points:
distinguishes X- and O-points:
- If
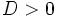 , then
, then 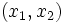 is an extremum (an O-point)
is an extremum (an O-point)
- If
 , then
, then 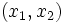 is a saddle point (an X-point)
is a saddle point (an X-point)
Using this method, all of the X- and O-points in the system can be identified.
X- and O-points in a plasma configuration are accompanied by features known as magnetic islands. These islands are regions of flux that are isolated from the rest of the configuration by a magnetic separatrix. An X-point is the location of closure for this separatrix, so the value of the flux function everywhere on the separatrix is equal to the value of the flux function at the X-point 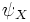 . An O-point will exist in the interior of the island.
. An O-point will exist in the interior of the island.
Because 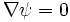 at X- and O-points, the magnetic field will be directed only along the direction of symmetry at these points and the time evolution equation for
at X- and O-points, the magnetic field will be directed only along the direction of symmetry at these points and the time evolution equation for 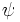 reduces to simply
reduces to simply
Examples
- Generals 2006, Part I, Problem 1
References
- ↑ Kusse, Bruce and Erik Westwig, Mathematical Physics, Wiley (1998). ISBN 0-471-15431-8
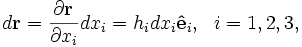
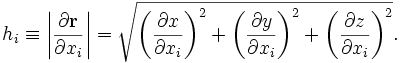
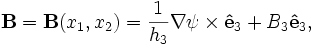
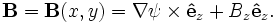
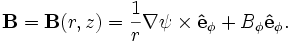
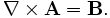
![\nabla\times\mathbf{A} = \frac{1}{h_2 h_3}\left[\frac{\partial(h_3 A_3)}{\partial x_2} - \frac{\partial(h_2 A_2)}{\partial x_3}\right] \mathbf{\hat{e}}_1
+ \frac{1}{h_1 h_3}\left[\frac{\partial(h_1 A_1)}{\partial x_3} - \frac{\partial(h_3 A_3)}{\partial x_1}\right]\mathbf{\hat{e}}_2 + B_3 \mathbf{\hat{e}}_3.](../../images/math/e/9/4/e941b8d88dedce81f67c7dd7352936b9.png)

+ B_3 \mathbf{\hat{e}}_3.](../../images/math/0/2/d/02d8bdeb890b33184d8deca85dd158df.png)
![\nabla\psi\times\mathbf{\hat{e}}_3 = \left[\frac{1}{h_1}\left(\frac{\partial \psi}{\partial x_1}\right) \mathbf{\hat{e}}_1
+ \frac{1}{h_2}\left(\frac{\partial \psi}{\partial x_2}\right) \mathbf{\hat{e}}_2\right]\times\mathbf{\hat{e}}_3
= \left[\frac{1}{h_2}\frac{\partial}{\partial x_2}\mathbf{\hat{e}}_1 - \frac{1}{h_1}\frac{\partial}{\partial x_1}\mathbf{\hat{e}}_2\right] \psi.](../../images/math/f/5/b/f5b065a478e4e0bdf70c8cc35916b8a3.png)
![\mathbf{B} = \frac{1}{h_3}\nabla\psi\times\mathbf{\hat{e}}_3 + B_3 \mathbf{\hat{e}}_3 =
\frac{1}{h_3}\left[\frac{1}{h_2}\frac{\partial}{\partial x_2}\mathbf{\hat{e}}_1 - \frac{1}{h_1}\frac{\partial}{\partial x_1}\mathbf{\hat{e}}_2\right] \psi
+ B_3 \mathbf{\hat{e}}_3.
:](../../images/math/5/4/f/54ff6e47341042204c17f1e23522e602.png)
![\frac{1}{h_3}\left[\frac{1}{h_2}\frac{\partial}{\partial x_2}\mathbf{\hat{e}}_1 - \frac{1}{h_1}\frac{\partial}{\partial x_1}\mathbf{\hat{e}}_2\right] (h_3 A_3 - \psi) = 0.](../../images/math/d/d/8/dd8a414cab98d1bdcbfeb436f1b603f7.png)
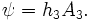
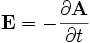
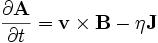
![\frac{\partial \psi}{\partial t} = h_3\frac{\partial A_3}{\partial t} = h_3\bigg[(\mathbf{v}\times\mathbf{B})_3 - \eta J_3\bigg]
= h_3\bigg[ v_2 B_1 - v_1 B_2 - \eta J_3\bigg] = h_3\left[\frac{v_2}{h_2 h_3}\frac{\partial\psi}{\partial x_2} - \frac{v_1}{h_1 h_3}\frac{\partial\psi}{\partial x_1} - \eta J_3\right],](../../images/math/a/0/5/a05e7d9e3907ca77109f61a6b86de52d.png)