Generalised Coordinates
From QED
Any s variables 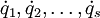 are known as generalised velocities.
are known as generalised velocities.
It is occasionally the case that elements within a system are constrained in one or more dimensions. It is often convenient to describe such systems in terms of a reduced number of generalised coordinates, matching the number of degrees of the system. More complicated constraints must be dealt with alternatively (perhaps using Lagrange multipliers).
The metric tensor is a tensor which, roughly (but accurately, for most purposes in physics), describes the distance from one point in a generalised coordinate system to another. For the purposes of classical mechanics, it is used most often to cast the generalised coordinates to cartesian coordinates, for example, in order to write the Lagrangian.
The Lagrangian is of the form L = T − U, where T is the kinetic energy. For free particles, 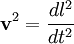 is the velocity in Cartesian space, and dl2 is the line element.
is the velocity in Cartesian space, and dl2 is the line element.
To obtain the Lagrangian for a system described by generialised coordinates, we require the following transformations:
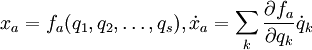 , etc.
, etc.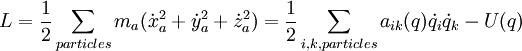 ,
where
,
where 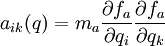
Orthogonal and Curvilinear coordinates have the interesting property that their metric tensor is diagonal, that is, gij = giiδij where δij is the Kronecker delta . As a result, the line element is
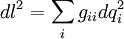
And thus
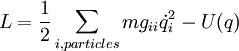
- Cylindrical Coordinates
- Spherical Coordinates
- Conical Coordinates
- Toridal Coordinates
- Curvilinear Coordinates
This page was recovered in October 2009 from the Plasmagicians page on Generalised_Coordinates dated 17:55, 11 October 2006.












