1999 I 1

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/1999 I 1]])
Jump to: navigation, search

We start with the dispersion relation:

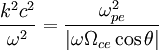
\frac{k^{2}c^{2}}{\omega^{2}}=\frac{\omega_{pe}^{2}}{\left|\omega\Omega_{ce}\cos\theta\right|}

Rearranging the dispersion relation:

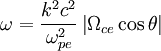
\omega=\frac{k^{2}c^{2}}{\omega_{pe}^{2}}\left|\Omega_{ce}\cos\theta\right|

So that the group velocity is:

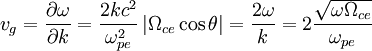
v_{g}=\frac{\partial\omega}{\partial k}=\frac{2kc^{2}}{\omega_{pe}^{2}}\left|\Omega_{ce}\cos\theta\right|=\frac{2\omega}{k}=2\frac{\sqrt{\omega\Omega_{ce}}}{\omega_{pe}}

Where in the last step we use the dipsersion relation and the fact that 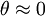\theta\approx0. This means that the higher frequencies will have a higher group velocity, and lower frequencies will have a lower group velocity. Thus, the higher frequencies will arrive at an observer first, and the lower frequencies later, making it seem that the tone is descending.

We start with:

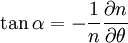
\tan\alpha=-\frac{1}{n}\frac{\partial n}{\partial\theta}

Where 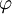\varphi the angle between the ray and the magnetic field. Plugging in the dispersion relation:

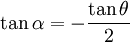
\tan\alpha=-\frac{\tan\theta}{2}

So the angle between the ray and the magnetic field is:

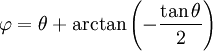
\varphi=\theta+\arctan\left(-\frac{\tan\theta}{2}\right)

Taking the derivative to find the max:

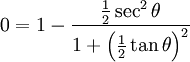
0=1-\frac{\frac{1}{2}\sec^{2}\theta}{1+\left(\frac{1}{2}\tan\theta\right)^{2}}

Using tan2θ + 1 = sec2θ:

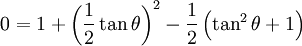
0=1+\left(\frac{1}{2}\tan\theta\right)^{2}-\frac{1}{2}\left(\tan^{2}\theta+1\right)

Or:

tan2θ = 8

This defines the maximum value that 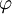\varphi can take. Therefore, the group velocity must flow approximately along the field lines, and so would tend to go between the northern and southern hemispheres, following the earth's magnetic field.

This page was recovered in October 2009 from the Plasmagicians page on Generals_1999_I_1 dated 22:27, 17 April 2007.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Generals/1999_I_1"
Personal tools