1999 I 4A
From QED
We have the system of equations for 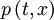 with c being a constant:
with c being a constant:
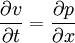
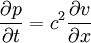
And the finite difference scheme:
![v_{j}^{n+1}=v_{j}^{n}+\frac{\delta t}{2\delta x}\left[p_{j+1}^{n}-p_{j-1}^{n}\right]](../../../images/math/3/3/e/33e59345df67eb8efe99788d72c839a8.png)
![p_{j}^{n+1}=p_{j}^{n}+\frac{c^{2}\delta t}{2\delta x}\left[v_{j+1}^{n}-v_{j-1}^{n}\right]](../../../images/math/4/6/5/46538bbf9f4bf9ddc629d14ed5191356.png)
If we substitute 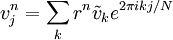 ,
,
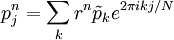 :
:
![\tilde{v}_{k}r=\tilde{v}_{k}+\frac{\delta t}{2\delta x}\left[\tilde{p}_{k}e^{2\pi ik/N}-\tilde{p}_{k}e^{-2\pi ik/N}\right]=\tilde{v}_{k}+\frac{i\delta t}{\delta x}\tilde{p}_{k}\sin\theta_{k}](../../../images/math/e/2/6/e2669bad3b91c6c0ef45fa0b3913e8db.png)
![\tilde{p}_{k}r=\tilde{p}_{k}+\frac{c^{2}\delta t}{2\delta x}\left[\tilde{v}_{k}e^{2\pi ik/N}-\tilde{v}_{k}e^{-2\pi ik/N}\right]=\tilde{p}_{k}+\frac{ic^{2}\delta t}{\delta x}\tilde{v}_{k}\sin\theta_{k}](../../../images/math/f/7/5/f75c05377717fd15defa5326396352a0.png)
With θk = 2πk / N. Combining the equations:
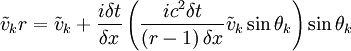
This gives:
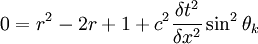
Solving for r:
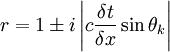
Or:
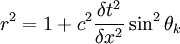
This means that for finite δt, δx,  is always > 1 for some k, making the method unstable.
is always > 1 for some k, making the method unstable.
If we use the scheme:
![v_{j}^{n+1}=v_{j}^{n}+\frac{\delta t}{2\delta x}\left[p_{j+1}^{n+1/2}-p_{j-1}^{n+1/2}\right]](../../../images/math/e/8/0/e80c296e6d8dfeb9961756a846cd415b.png)
![p_{j}^{n+1/2}=p_{j}^{n-1/2}+\frac{c^{2}\delta t}{2\delta x}\left[v_{j+1}^{n}-v_{j-1}^{n}\right]](../../../images/math/a/3/7/a37018e4292093217f379de0d9e2cf08.png)
We get:
![\tilde{v}_{k}r=\tilde{v}_{k}+\frac{\delta t}{2\delta x}r^{1/2}\left[\tilde{p}_{k}e^{2\pi ik/N}-\tilde{p}_{k}e^{-2\pi ik/N}\right]=\tilde{v}_{k}+\frac{i\delta t}{\delta x}r^{1/2}\tilde{p}_{k}\sin\theta_{k}](../../../images/math/d/9/7/d97db51503b8fad5abe1c484506e8880.png)
![\tilde{p}_{k}r=\tilde{p}_{k}+\frac{c^{2}\delta t}{2\delta x}r^{1/2}\left[\tilde{v}_{k}e^{2\pi ik/N}-\tilde{v}_{k}e^{-2\pi ik/N}\right]=\tilde{p}_{k}+\frac{ic^{2}\delta t}{\delta x}r^{1/2}\tilde{v}_{k}\sin\theta_{k}](../../../images/math/5/6/3/5637a2e2db9b0a135760e19c4d610b81.png)
And then combining:
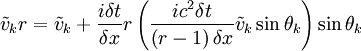
Or:
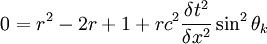
Which gives:
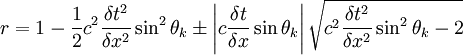
At θk = π / 2:
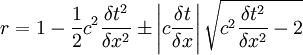
So that, for 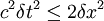 :
:
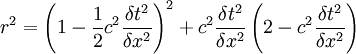
So that if:
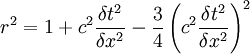
Our condition becomes:
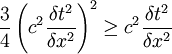
Or:
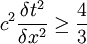
For 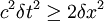 :
:
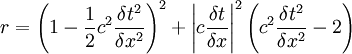
Or:
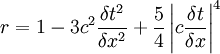
For stability:
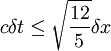
Combining the conditions:
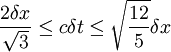
This page was recovered in October 2009 from the Plasmagicians page on Generals_1999_I_4A dated 22:29, 17 April 2007.












