2000 II 2
From QED
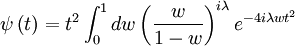
Writing this as:
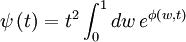
With:
![\phi\left(w,t\right)=i\lambda\left[\ln\left(w\right)-\ln\left(1-w\right)-4wt^{2}\right]](../../../images/math/4/b/1/4b159a7da27cb30dfe3fc1605f30b446.png)
Setting the derivative to zero to find saddles:
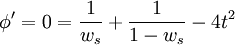
Rearranging:
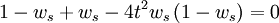
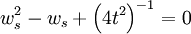
Solving for ws:
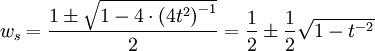
Which we will now call 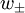 . Looking at the second derivative:
. Looking at the second derivative:
![\phi^{\prime\prime}\left(w\right)=i\lambda\left[-\frac{1}{w^{2}}+\frac{1}{\left(1-w\right)^{2}}\right]](../../../images/math/8/a/0/8a0c27540a0888c8b857543fe6b54a40.png)
So that:
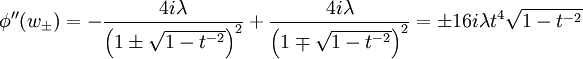
For 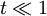 , the saddle points are off the axis. Taylor expanding:
, the saddle points are off the axis. Taylor expanding:
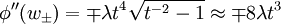
So the direction 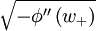 is along the real axis and the direction
is along the real axis and the direction 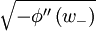 is purely imaginary and cannot be used. We then get from the saddle
at w + :
is purely imaginary and cannot be used. We then get from the saddle
at w + :
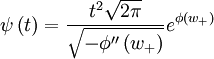
Expressing 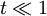 :
:
![\phi\left(w_{+},t\right)=i\lambda\left[\ln\left(\frac{1+\sqrt{1-t^{-2}}}{1-\sqrt{1-t^{-2}}}\right)-4\left(1+\sqrt{1-t^{-2}}\right)t^{2}\right]\approx i\lambda\left[\ln\left(-1\right)-4it\right]=4\lambda t-\lambda\pi](../../../images/math/5/b/3/5b3ac64a836b3b853f61d34188530ac7.png)
Putting this in:
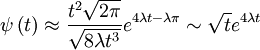
For 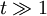 , the saddle points are on the real axis. Finding the
second derivative:
, the saddle points are on the real axis. Finding the
second derivative:
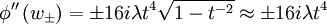
So the direction of integration is 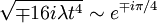 .
.
We integrate through both saddles. Evaluating φ at the first
saddle, with 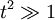 :
:
![\phi\left(w_{+},t\right)=i\lambda\left[\ln\left(\frac{1+\sqrt{1-t^{-2}}}{1-\sqrt{1-t^{-2}}}\right)-4\left(1+\sqrt{1-t^{-2}}\right)t^{2}\right]\approx i\lambda\left[\ln\left(\frac{2}{t^{-2}/2}\right)-8t^{2}\right]=2i\lambda\ln\left(2t\right)+8i\lambda t^{2}](../../../images/math/1/c/a/1ca37b681b98b959be68d14e8987b958.png)
So this is just a phase factor. At the other saddle:
![\phi\left(w_{-},t\right)=i\lambda\left[\ln\left(\frac{1-\sqrt{1-t^{-2}}}{1+\sqrt{1-t^{-2}}}\right)-4\left(1+\sqrt{1-t^{-2}}\right)t^{2}\right]\approx i\lambda\left[\ln\left(\frac{t^{-2}/2}{2}\right)-8t^{2}\right]=-2i\lambda\ln\left(t/2\right)+8i\lambda t^{2}](../../../images/math/b/2/9/b29b3a37800f7849e48aeca3f74f85b4.png)
So this is another phase factor. Then the saddles contributions are:
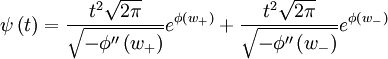
Plugging in:
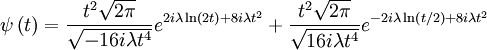
Which simplifies to:
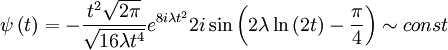
This page was recovered in October 2009 from the Plasmagicians page on Generals_2000_II_2 dated 02:50, 29 April 2007.












