2001 II 5
From QED
The electrostatic approximation assumes that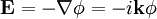 
.
This is valid for short wavelengths. The condition is that 
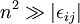for all elements of the dielectric tensor 
.
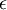The perturbed distribution function is:
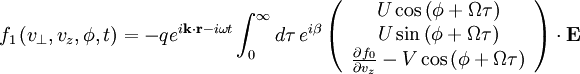
With
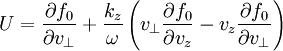
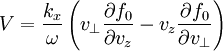
![\beta=-\frac{k_{x}v_{\perp}}{\omega}\left[\sin\left(\phi+\Omega\tau\right)-\sin\phi\right]+\left(\omega-k_{z}v_{z}\right)\tau](../../../images/math/7/7/b/77b4a275cc808d9d624c86b2cd785f6d.png)
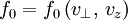
The electrostatic approximation gives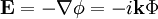 
.
Then:
Rewriting the distribution function:
![\begin{array}{rcl} f_{1}\left(v_{\perp},v_{z},\phi,t\right) = -qe^{i\mathbf{k}\cdot\mathbf{r}-i\omega t}\int_{0}^{\infty}d\tau\, e^{-ik_{x}v_{\perp}\left[\sin\left(\phi+\Omega\tau\right)-\sin\phi\right]/\omega+i\left(\omega-k_{z}v_{z}\right)\tau}\cdot\\ \left[-ik_{x}\Phi U\cos\left(\phi+\Omega\tau\right)-ik_{z}\Phi\frac{\partial f_{0}}{\partial v_{z}}+ik_{z}\Phi V\cos\left(\phi+\Omega\tau\right)\right]\end{array}](../../../images/math/d/0/5/d05648d462f03593c368aef17d7e3a56.png)
Integrating over angles φ:
![\begin{array}{rcl} f_{1}\left(v_{\perp},v_{z},t\right) = 2\pi iqe^{i\mathbf{k}\cdot\mathbf{r}-i\omega t}\sum_{n=-\infty}^{\infty}\int_{0}^{\infty}d\tau\, e^{i\left(\omega-k_{z}v_{z}\right)\tau}e^{-in\Omega\tau}\cdot\\ J_{n}^{2}\left(\frac{k_{x}v_{\perp}}{\omega}\right)\left[k_{x}\Phi U\frac{n\omega}{k_{x}v_{\perp}}+k_{z}\Phi\frac{\partial f_{0}}{\partial v_{z}}-k_{z}\Phi V\frac{n\omega}{k_{x}v_{\perp}}\right]\end{array}](../../../images/math/5/9/0/590f7bd47ca278244ff506c75e2664fb.png)
If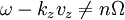 
, this integral will average out
to 0. Otherwise the integral is infinity. This gives:
![\begin{array}{rcl} f_{1}\left(v_{\perp},v_{z},t\right) = 2\pi iqe^{i\mathbf{k}\cdot\mathbf{r}-i\omega t}\sum_{n=-\infty}^{\infty}J_{n}^{2}\left(\frac{k_{x}v_{\perp}}{\omega}\right)\cdot\\ \left[k_{x}\Phi U\frac{n\omega}{k_{x}v_{\perp}}+k_{z}\Phi\frac{\partial f_{0}}{\partial v_{z}}-k_{z}\Phi V\frac{n\omega}{k_{x}v_{\perp}}\right]\end{array}](../../../images/math/4/4/1/4415d7d0c0acf71ef380b791feb004d0.png)
Integrating over velocity space:
![\begin{array}{rcl} n_{1}\left(t\right) = \int v_{\perp}dv_{\perp}\int dv_{z}\,2\pi iqe^{i\mathbf{k}\cdot\mathbf{r}-i\omega t}\sum_{n=-\infty}^{\infty}\delta\left(\omega-k_{z}v_{z}-n\Omega\right)\cdot\\ J_{n}^{2}\left(\frac{k_{x}v_{\perp}}{\omega}\right)\left[k_{x}\Phi U\frac{n\omega}{k_{x}v_{\perp}}+k_{z}\Phi\frac{\partial f_{0}}{\partial v_{z}}-k_{z}\Phi V\frac{n\omega}{k_{x}v_{\perp}}\right]\end{array}](../../../images/math/b/d/e/bde75a81358afee31c6e19b356151a5c.png)
One integral is over a delta function:
![\begin{array}{rcl} n_{1}\left(t\right) = \int dv_{\perp}\, v_{\perp}2\pi iqe^{i\mathbf{k}\cdot\mathbf{r}-i\omega t}\sum_{n=-\infty}^{\infty}J_{n}^{2}\left(\frac{k_{x}v_{\perp}}{\omega}\right)\cdot\\ \left[k_{x}\Phi U\frac{n\omega}{k_{x}v_{\perp}}+k_{z}\Phi\frac{\partial f_{0}}{\partial v_{z}}-k_{z}\Phi V\frac{n\omega}{k_{x}v_{\perp}}\right]_{v_{z}=\left(\omega-n\Omega\right)/k_{z}}\end{array}](../../../images/math/3/3/b/33bf2ee1c31651ebdcceae0abd748602.png)
Using Poisson's equation:
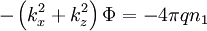
So:
![\begin{array}{rcl} \left(k_{x}^{2}+k_{z}^{2}\right) = 8\pi^{2}iq^{2}e^{i\mathbf{k}\cdot\mathbf{r}-i\omega t}\int dv_{\perp}\, v_{\perp}\sum_{n=-\infty}^{\infty}J_{n}^{2}\left(\frac{k_{x}v_{\perp}}{\omega}\right)\cdot\\ \left[k_{x}U\frac{n\omega}{k_{x}v_{\perp}}+k_{z}\frac{\partial f_{0}}{\partial v_{z}}-k_{z}V\frac{n\omega}{k_{x}v_{\perp}}\right]_{v_{z}=\left(\omega-n\Omega\right)/k_{z}}\end{array}](../../../images/math/b/d/8/bd81239d8d6d4eecfb4fb97b5768c893.png)
This page was recovered in October 2009 from the Plasmagicians page on Generals_2001_II_5 dated 19:45, 25 April 2007.
