Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

2002 II 7

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2002 II 7]])

Jump to: navigation, search

THIS IS PROBABLY WRONG (Grad11)

We have the wave equation:

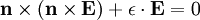
$\mathbf{n}\times\left(\mathbf{n}\times\mathbf{E}\right)+\epsilon\cdot\mathbf{E}=0$

For transverse waves, this becomes:

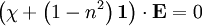
$\left(\chi+\left(1-n^{2}\right)\mathbf{1}\right)\cdot\mathbf{E}=0$

We can take the first two equations:

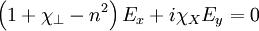
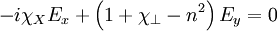
$\left(1+\chi_{\perp}-n^{2}\right)E_{x}+i\chi_{X}E_{y}=0$ $-i\chi_{X}E_{x}+\left(1+\chi_{\perp}-n^{2}\right)E_{y}=0$

And combine them:

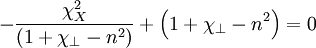
$-\frac{\chi_{X}^{2}}{\left(1+\chi_{\perp}-n^{2}\right)}+\left(1+\chi_{\perp}-n^{2}\right)=0$

Expanding:

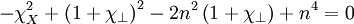
$-\chi_{X}^{2}+\left(1+\chi_{\perp}\right)^{2}-2n^{2}\left(1+\chi_{\perp}\right)+n^{4}=0$

Which can be factored to:

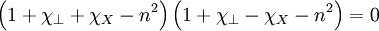
$\left(1+\chi_{\perp}+\chi_{X}-n^{2}\right)\left(1+\chi_{\perp}-\chi_{X}-n^{2}\right)=0$

Plugging in:

$\chi_{\perp}=\sum_{s}\frac{1}{2}\frac{\omega_{p}^{2}}{\omega^{2}}\zeta_{0}\left[Z\left(\zeta_{1}\right)+Z\left(\zeta_{-1}\right)\right]$ $\chi_{X}=\sum_{s}\frac{1}{2}\frac{\omega_{p}^{2}}{\omega^{2}}\zeta_{0}\left[Z\left(\zeta_{1}\right)-Z\left(\zeta_{-1}\right)\right]$

We get:

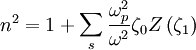
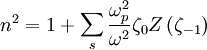
$n^{2}=1+\sum_{s}\frac{\omega_{p}^{2}}{\omega^{2}}\zeta_{0}Z\left(\zeta_{1}\right)$ $n^{2}=1+\sum_{s}\frac{\omega_{p}^{2}}{\omega^{2}}\zeta_{0}Z\left(\zeta_{-1}\right)$

The wave electric field will be unpolarized, since $E x, E y = 0$ . We get the dispersion relation for longitudinal waves:

ε z z = 0

This gives:

1 + χ z z = 0

The dispersion relation was:

1 + χ z z = 0

Plugging in:

$-1=\sum_{s}\frac{2\omega_{ps}^{2}}{k_{\|}^{2}v_{ts}^{2}}\left[1+\frac{\omega-k_{\|}v_{Ds}}{k_{\|}v_{ts}}Z\left(\zeta_{0}^{\left(s\right)}\right)\right]$

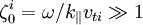For ions, $\zeta_{0}^{i}=\omega/k_{\|}v_{ti}\gg1$ . We can take the expansion for the ion term then:

$-1=\frac{2\omega_{pe}^{2}}{k_{\|}^{2}v_{te}^{2}}\left[1+\frac{\omega-k_{\|}v_{D}}{k_{\|}v_{te}}Z\left(\zeta_{0}^{\left(e\right)}\right)\right]+\frac{2\omega_{pi}^{2}}{k_{\|}^{2}v_{ti}^{2}}\left[1+\frac{\omega}{k_{\|}v_{ti}}\left(i\sigma\sqrt{\pi}e^{-\zeta_{i}^{2}}-\frac{k_{\|}v_{ti}}{\omega}\left(1+\frac{k_{\|}^{2}v_{ti}^{2}}{2\omega^{2}}\right)\right)\right]$

Which becomes, discarding the exponential which is small:

$-1=\frac{2\omega_{pe}^{2}}{k_{\|}^{2}v_{te}^{2}}\left[1+\frac{\omega-k_{\|}v_{D}}{k_{\|}v_{te}}Z\left(\zeta_{0}^{\left(e\right)}\right)\right]+\frac{\omega_{pi}^{2}}{\omega^{2}}$

Multiplying through by 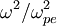$\omega^{2}/\omega_{pe}^{2}$ , the last term is small (since it goes like the mass ratio $m e / m i$ ), and we find:

$\frac{\omega^{2}}{\omega_{pe}^{2}}=\frac{2}{k_{\|}^{2}v_{te}^{2}}\left[1+\frac{\omega-k_{\|}v_{D}}{k_{\|}v_{te}}Z\left(\zeta_{0}^{\left(e\right)}\right)\right]$

Writing $ω = ω r + i γ$ :

$\frac{\omega_{r}^{2}+2i\gamma\omega_{r}-\gamma^{2}}{\omega_{pe}^{2}}=\frac{2}{k_{\|}^{2}v_{te}^{2}}\left[1+\frac{\omega_{r}+i\gamma-k_{\|}v_{D}}{k_{\|}v_{te}}Z\left(\zeta_{0}^{\left(e\right)}\right)\right]$

Then, setting the imaginary part of both sides equal:

$\frac{2i\gamma\omega_{r}}{\omega_{pe}^{2}}=\frac{2}{k_{\|}^{2}v_{te}^{2}}\frac{\omega_{r}}{k_{\|}v_{te}}\mathrm{Im}\left[Z\left(\zeta_{0}^{\left(e\right)}\right)\right]$

Or: