2002 I 1
From QED
The magnetic field is:
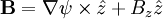
The equilibrium momentum equation gives:
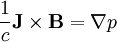
Using:
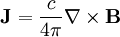
Plugging in:
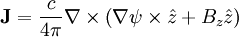
Using vector identities:
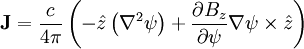
Plugging this in:
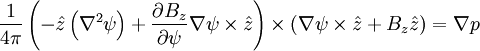
Or:
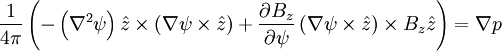
Expanding:
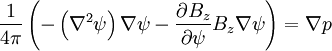
Since the only vector on the left is 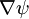 , p is a function
only of ψ, and we can write
, p is a function
only of ψ, and we can write 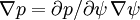 ,
and dot with
,
and dot with 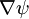 :
:
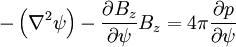
Or:
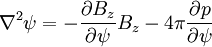
In slab coordinates:
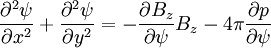
We choose the equilibrium:
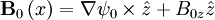
We are given:
From the 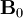 definition:
definition:
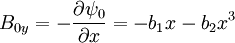
So:
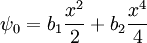
The current is:
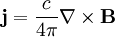
So:
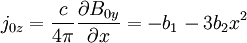
The equilibrium equation becomes for p = 0:
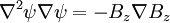
If we take the curl (to get rid of the unknown Bz term):
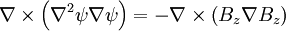
Writing this out:
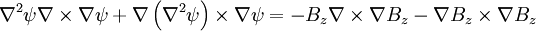
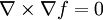 for any scalar function:
for any scalar function:
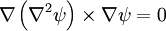
This gives the first order equation:
![\nabla\left(\nabla^{2}\psi_{0}\right)\times\nabla\left[\psi_{1}\cos ky\right]+\nabla\left[\nabla^{2}\left(\psi_{1}\cos ky\right)\right]\times\nabla\psi_{0}=0](../../../images/math/9/0/2/9021b8facfb8234d3b8f79b2d3c56a32.png)
Since ψ1 and ψ0 are only functions of x:
![\left(\psi_{0}^{\prime\prime\prime}\hat{x}\right)\times\left(\hat{x}\psi_{1}^{\prime}\cos ky-\hat{y}k\psi_{1}\sin ky\right)+\nabla\left[\psi_{1}^{\prime\prime}\cos ky-k^{2}\psi_{1}\cos ky\right]\times\left(\hat{x}\psi_{0}^{\prime}\right)=0](../../../images/math/3/6/0/3602881e75abfac4e74cc0c8536ff9d6.png)
Dotting with 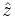 (the only nonzero component):
(the only nonzero component):
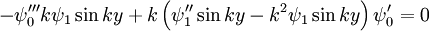
Or:
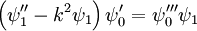
Using 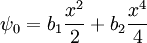 :
:
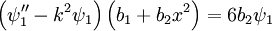
We write:
at the boundary:
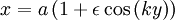
So:
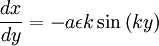
And:
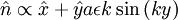
At the other boundary:
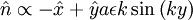
So:
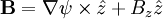
The boundary condition:
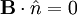
At the upper boundary:
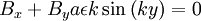
Putting in the definition for the B:
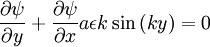
Using 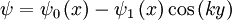 :
:
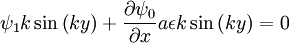
Simplifying:
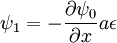
At the lower boundary, we get by analogy:
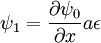
So:
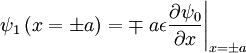
For the equation:
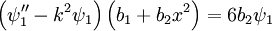
Near x = 0:
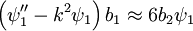
Which can be written as:
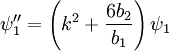
We get:
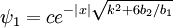
The jump condition across the boundary will be:
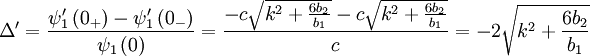
If b2 = 0:
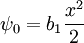
Using the boundary conditions gives:
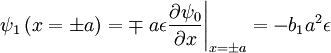
Which gives the exterior solution:
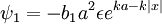
So that the total flux function is:
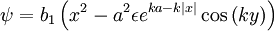
Near x = 0:
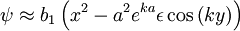
O- and X-points then occur where 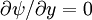 :
:
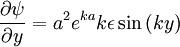
So points occur at ky = nπ, x = 0. O-points are minima, and X-points are maxima:
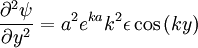
Failed to parse (syntax error): \partial^{2}\psi/\partial y^{2}>0
at ky = 2πn, so these are
O-points. 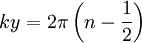 ,
so these points are X-points.
,
so these points are X-points.
This page was recovered in October 2009 from the Plasmagicians page on Generals_2002_I_1 dated 19:55, 27 April 2007.












