2002 I 2
From QED
We have the equation:
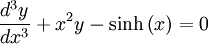
The homogenous equation is:
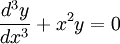
Taking y˜eS:
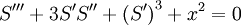
Taking a balance between 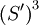 and x2,
and x2,
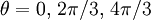 .
Then
.
Then 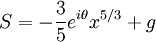 :
:
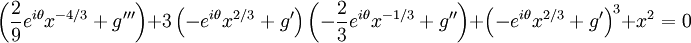
Expanding:
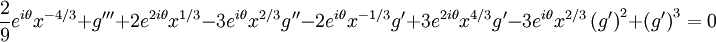
Balance between 2e2iθx1 / 3 and 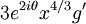 gives
gives 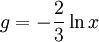 . The
homogenous solution can then be written:
. The
homogenous solution can then be written:
![y_{homog}=Ae^{-3x^{5/3}/5}+\left[B\sin\left(\frac{3\sqrt{3}x^{5/3}}{10}\right)+C\cos\left(\frac{3\sqrt{3}x^{5/3}}{10}\right)\right]e^{3x^{5/3}/10}](../../../images/math/8/7/9/879c7b71f509e90d3b704289d9667f6d.png)
The inhomogenous equation is:
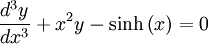
For large x, the last homogenous terms dominate (since they go
like 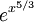 ), unless B = C = 0. Then we guess a balance between
x2y and ex / 2, giving:
), unless B = C = 0. Then we guess a balance between
x2y and ex / 2, giving:
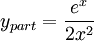
Which does dominate. The general solution is then:
![y=Ae^{-3x^{5/3}/5}+\left[B\sin\left(\frac{3\sqrt{3}x^{5/3}}{10}\right)+C\cos\left(\frac{3\sqrt{3}x^{5/3}}{10}\right)\right]e^{3x^{5/3}/10}+\frac{1}{2x^{2}}e^{x}](../../../images/math/8/c/1/8c12c07bc09ac2c9dfb2ddb22a7a22ec.png)
This page was recovered in October 2009 from the Plasmagicians page on Generals_2002_I_2 dated 20:13, 25 April 2007.












