2002 I 6
From QED
This solution is so close and yet so far... also, that's not how integration by parts works.
The trapping condition at the z = − L side is from the magnetic confinement,
so it is given by E < μBmax. Writing this out in terms of 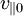 and
and 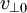 :
:
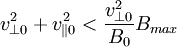
The trapping condition at z = + L is simply 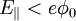 . This gives:
. This gives:
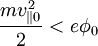
The particles will leave at z = − L for 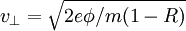 , which gives E = eφ(2 − R) / (1 − R).
, which gives E = eφ(2 − R) / (1 − R).
In the presence of pitch-angle scattering, particles will leave at z = + L for E < eφ(2 − R) / (1 − R), and at z = − L for E > eφ(2 − R) / (1 − R).
If the bounce frequency is much greater than the collision frequency, then it is possible to neglect the exact position of the particles and consider them as filling the space uniformally. One would also have to assume that the collision frequency is dependent on only the particle energy, not the specific pitch angle, magnetic field strength, or electric potential. This is a good approximation.
We can treat the collisions as occuring at the midplane, since the particle will pass through the midplane either just before or just after the collision. A change in the pitch angle by θ at position z = z0 will be equivalent to a collision that changes the pitch angle by θ at the midplane (z = 0).
If we write the Vlasov equation:
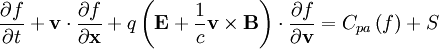
Since f is only a function of v, μ, and t, 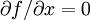 .
Also, if we only treat collisions at the midplane, E = 0. Lastly,
.
Also, if we only treat collisions at the midplane, E = 0. Lastly,
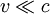 , so we discard the magnetic field term:
, so we discard the magnetic field term:
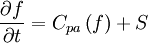
The boundary condition for z = − L becomes:
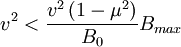
The boundary conditions are that 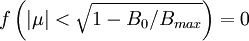 and
and 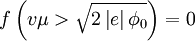 .
.
Writing out the differential equation:
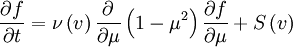
Solving the homogenous equation in μ:
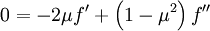
So that:
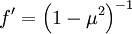
Then split:
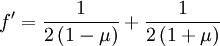
So:
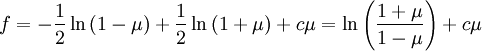
In steady state:
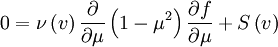
We use the solution:
![f=A\left(\nu\right)\left[\ln\left(1+\mu\right)+b\ln\left(1-\mu\right)\right]](../../../images/math/7/3/2/7328ce16490b98fb5c09f1934cd42587.png)
Plugging in:
![0=\nu\left(v\right)A\left(\nu\right)\frac{\partial}{\partial\mu}\left[-\left(1-\mu\right)+b\left(1+\mu\right)\right]+S\left(v\right)](../../../images/math/5/3/1/531e61090d46bc74cde6ad4be1e06542.png)
Setting b = 1:
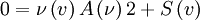
So:
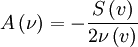
The steady state solution is:
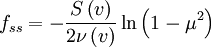
If we insert the boundary condition 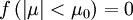 ,
letting:
,
letting:
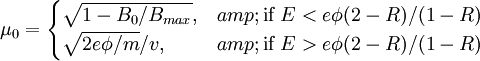
We get:
![f=-\frac{S\left(v\right)}{2\nu\left(v\right)}\ln\left(1-\mu^{2}\right)\left[\Theta\left(\mu+\mu_{0}\right)-\Theta\left(\mu-\mu_{0}\right)\right]](../../../images/math/1/d/0/1d07abc10aa8dc693aaf09d37ca327fd.png)
The number of particles in the system is:
![n\left(v\right)=-\int_{-1}^{1}d\mu\frac{S\left(v\right)}{2\nu\left(v\right)}\ln\left(1-\mu^{2}\right)\left[\Theta\left(\mu+\mu_{0}\right)-\Theta\left(\mu-\mu_{0}\right)\right]](../../../images/math/8/9/e/89e2a8cde066b2e4c628bd6c6ff2d511.png)
Integrating by parts:
![n\left(v\right)=\int_{-1}^{1}d\mu\frac{S\left(v\right)}{2\nu\left(v\right)}\frac{-2\mu}{1-\mu^{2}}\left[\delta\left(\mu+\mu_{0}\right)-\delta\left(\mu-\mu_{0}\right)\right]](../../../images/math/0/b/c/0bc69dffa4f4b865670c8f15aff7029b.png)
Integrating:
![n\left(v\right)=\frac{S\left(v\right)}{2\nu\left(v\right)}\left[\frac{2\mu_{0}}{1-\mu_{0}^{2}}+\frac{2\mu_{0}}{1-\mu_{0}^{2}}\right]=\frac{S\left(v\right)}{\nu\left(v\right)}\left(\frac{\mu_{0}}{1-\mu_{0}^{2}}\right)](../../../images/math/a/9/a/a9a8d9bcb1d737cf200caa5c14d53112.png)
So the time in the system is:
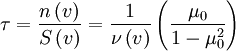
Plugging in for μ0 if E < eφ(2 − R) / (1 − R):
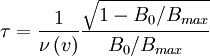
Plugging in for μ0 if E > eφ(2 − R) / (1 − R):
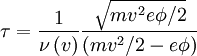
This page was recovered in October 2009 from the Plasmagicians page on Generals_2002_I_6 dated 20:59, 27 April 2007.












