Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

2003 II 1A

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2003 II 1A]])

Jump to: navigation, search

The algorithm is:

$U_{j}^{\star}=U_{j}^{n}-\frac{\delta t}{\delta x}\left[F_{j}^{n}-F_{j-1}^{n}\right]$ $U_{j}^{n+1}=\frac{1}{2}\left\{ U_{j}^{n}+U_{j}^{\star}-\frac{\delta t}{\delta x}\left[F_{j}^{\star}-F_{j-1}^{\star}\right]-\frac{\delta t}{\delta x}\left[F_{j}^{n}-2F_{j-1}^{n}+F_{j-2}^{n}\right]\right\}$

The linearized form of equation 1 is:

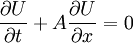
$\frac{\partial U}{\partial t}+A\frac{\partial U}{\partial x}=0$

Plugging in 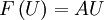$F\left(U\right)=AU$ :

$U_{j}^{\star}=U_{j}^{n}-\frac{\delta t}{\delta x}A\left[U_{j}^{n}-U_{j-1}^{n}\right]$ $U_{j}^{n+1}=\frac{1}{2}\left\{ U_{j}^{n}+U_{j}^{\star}-\frac{\delta t}{\delta x}A\left[U_{j}^{\star}-U_{j-1}^{\star}\right]-\frac{\delta t}{\delta x}A\left[U_{j}^{n}-2U_{j-1}^{n}+U_{j-2}^{n}\right]\right\}$

Taylor expanding around 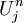$U_{j}^{n}$ :

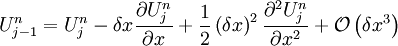
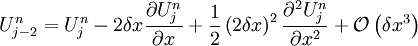
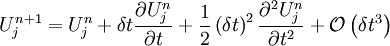
$U_{j-1}^{n}=U_{j}^{n}-\delta x\frac{\partial U_{j}^{n}}{\partial x}+\frac{1}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)$ $U_{j-2}^{n}=U_{j}^{n}-2\delta x\frac{\partial U_{j}^{n}}{\partial x}+\frac{1}{2}\left(2\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)$ $U_{j}^{n+1}=U_{j}^{n}+\delta t\frac{\partial U_{j}^{n}}{\partial t}+\frac{1}{2}\left(\delta t\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial t^{2}}+\mathcal{O}\left(\delta t^{3}\right)$ Plugging into the first step: $U_{j}^{\star}=U_{j}^{n}-\frac{\delta t}{\delta x}A\left[\delta x\frac{\partial U_{j}^{n}}{\partial x}-\frac{1}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)\right]$

We also find:

$U_{j-1}^{\star}=U_{j-1}^{n}-\frac{\delta t}{\delta x}A\left[U_{j-1}^{n}-U_{j-2}^{n}\right]$

Which gives:

$U_{j-1}^{\star}=U_{j}^{n}-\delta x\frac{\partial U_{j}^{n}}{\partial x}+\frac{1}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)-\frac{\delta t}{\delta x}A\left[\delta x\frac{\partial U_{j}^{n}}{\partial x}-\frac{3}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)\right]$

Plugging into terms in the second step:

$U_{j}^{n}+U_{j}^{\star}=2U_{j}^{n}-\frac{\delta t}{\delta x}A\left[\delta x\frac{\partial U_{j}^{n}}{\partial x}-\frac{1}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)\right]$ $U_{j}^{\star}-U_{j-1}^{\star}=\delta x\frac{\partial U_{j}^{n}}{\partial x}-\frac{1}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}-\frac{\delta t}{\delta x}A\left[\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)\right]$ $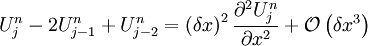U_{j}^{n}-2U_{j-1}^{n}+U_{j-2}^{n}=\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)$

Then writing 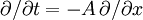$\partial/\partial t=-A\,\partial/\partial x$ :

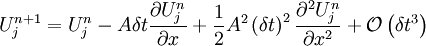
$U_{j}^{n+1}=U_{j}^{n}-A\delta t\frac{\partial U_{j}^{n}}{\partial x}+\frac{1}{2}A^{2}\left(\delta t\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta t^{3}\right)$

Step 2 then becomes:

$\begin{array}{rcl} -2A\delta t\frac{\partial U_{j}^{n}}{\partial x}+A^{2}\left(\delta t\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta t^{3}\right) & = & -\frac{\delta t}{\delta x}A\left[\delta x\frac{\partial U_{j}^{n}}{\partial x}-\frac{1}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)\right]\\ & & -\frac{\delta t}{\delta x}A\left[\delta x\frac{\partial U_{j}^{n}}{\partial x}-\frac{1}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}-\frac{\delta t}{\delta x}A\left[\frac{3}{2}\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)\right]\right]\\ & & -\frac{\delta t}{\delta x}A\left[\left(\delta x\right)^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x^{3}\right)\right]\end{array}$

Most terms cancel on the right, giving:

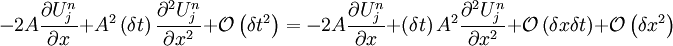
$-2A\frac{\partial U_{j}^{n}}{\partial x}+A^{2}\left(\delta t\right)\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta t^{2}\right)=-2A\frac{\partial U_{j}^{n}}{\partial x}+\left(\delta t\right)A^{2}\frac{\partial^{2}U_{j}^{n}}{\partial x^{2}}+\mathcal{O}\left(\delta x\delta t\right)+\mathcal{O}\left(\delta x^{2}\right)$

Becoming:

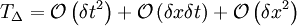
$T_{\Delta}=\mathcal{O}\left(\delta t^{2}\right)+\mathcal{O}\left(\delta x\delta t\right)+\mathcal{O}\left(\delta x^{2}\right)$

Going back to the first step:

$U_{j}^{\star}=U_{j}^{n}-\frac{\delta t}{\delta x}A\left[U_{j}^{n}-U_{j-1}^{n}\right]$

Setting $θ k = k j δ x / L$ :

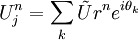
$U_{j}^{n}=\sum_{k}\tilde{U}r^{n}e^{i\theta_{k}}$

We get:

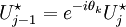
$U_{j}^{\star}=\tilde{U}-\frac{\delta t}{\delta x}A\tilde{U}\left[1-e^{-i\theta_{k}}\right]$ $U_{j-1}^{\star}=e^{-i\theta_{k}}U_{j}^{\star}$

So:

$r=\frac{1}{2}\left\{ 1+1-\frac{\delta t}{\delta x}A\left[1-e^{-i\theta_{k}}\right]-\frac{\delta t}{\delta x}A\left[1-e^{-i\theta_{k}}-\frac{\delta t}{\delta x}A\left[1-e^{-i\theta_{k}}\right]^{2}\right]-\frac{\delta t}{\delta x}A\left[1-2e^{-i\theta_{k}}+e^{-2i\theta_{k}}\right]\right\}$

Multiplying through by 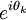$e^{i\theta_{k}}$ :

$2re^{i\theta_{k}}=2e^{i\theta_{k}}-\frac{\delta t}{\delta x}A\left[e^{i\theta_{k}}-1\right]-\frac{\delta t}{\delta x}A\left[e^{i\theta_{k}}-1-\frac{\delta t}{\delta x}A\left[e^{i\theta_{k}/2}-e^{-i\theta_{k}/2}\right]^{2}\right]-\frac{\delta t}{\delta x}A\left[e^{i\theta_{k}}-2+e^{-i\theta_{k}}\right]$

Using $sin$ and $cos$ :

$2re^{i\theta_{k}}=2e^{i\theta_{k}}-2\frac{\delta t}{\delta x}A\left[e^{i\theta_{k}}-1\right]-4\left(\frac{\delta t}{\delta x}A\right)^{2}\sin^{2}\left(\theta_{k}/2\right)-2\frac{\delta t}{\delta x}A\left[\cos\theta_{k}-1\right]$

Now solving for $r$ :

$r=1-\frac{\delta t}{\delta x}A\left[1-e^{-i\theta_{k}}\right]-2e^{-i\theta_{k}}\left(\frac{\delta t}{\delta x}A\right)^{2}\sin^{2}\left(\theta_{k}/2\right)-e^{-i\theta_{k}}\frac{\delta t}{\delta x}A\left[\cos\theta_{k}-1\right]$

This means:

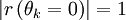
$\left|r\left(\theta_{k}=0\right)\right|=1$ $\left|r\left(\theta_{k}=\frac{\pi}{2}\right)\right|^{2}=\left\{ 1-\frac{\delta t}{\delta x}A\right\} ^{2}+\left\{ -\frac{\delta t}{\delta x}A+2\left(\frac{\delta t}{\delta x}A\right)^{2}\frac{1}{2}-\frac{\delta t}{\delta x}A\right\} ^{2}=\left[1-\frac{\delta t}{\delta x}A\right]^{2}+\left(\frac{\delta t}{\delta x}A\right)^{2}\left[\left(\frac{\delta t}{\delta x}A\right)-2\right]^{2}$

Whatever. Plotting graphically we just get the Courant condition:

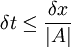
$\delta t\leq\frac{\delta x}{\left|A\right|}$

Then at $θ k = π$ :

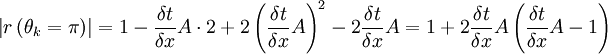
$\left|r\left(\theta_{k}=\pi\right)\right|=1-\frac{\delta t}{\delta x}A\cdot2+2\left(\frac{\delta t}{\delta x}A\right)^{2}-2\frac{\delta t}{\delta x}A=1+2\frac{\delta t}{\delta x}A\left(\frac{\delta t}{\delta x}A-1\right)$

Again giving the Courant condition.

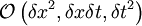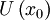The advantage of this method is that it is accurate to $\mathcal{O}\left(\delta x^{2},\delta x\delta t,\delta t^{2}\right)$ . A disadvantage is that because $U\left(x_{0}\right)$ only depends on the values of $U$ for $x < x 0$ , nothing can propagate backwards. This would be a problem if $A < 0$ .