2003 II 2

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2003 II 2]])
Jump to: navigation, search

Drift will primarily come from the 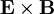\mathbf{E}\times\mathbf{B} term:

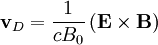
\mathbf{v}_{D}= \frac{1}{cB_{0}}\left(\mathbf{E}\times\mathbf{B}\right)

So that the radial term is:

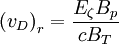
\left(v_{D}\right)_{r}=\frac{E_{\zeta}B_{p}}{cB_{T}}

The canonical angular momentum is:

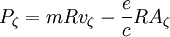
P_{\zeta}=mRv_{\zeta}-\frac{e}{c}RA_{\zeta}

Since \mathbf{B}=\nabla\times\mathbf{A}:

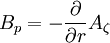
B_{p}=-\frac{\partial}{\partial r}A_{\zeta}

And so:

ψ = − RAζ

Giving:

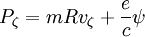
P_{\zeta}=mRv_{\zeta}+\frac{e}{c}\psi

We then solve for ψ :

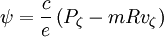
\psi=\frac{c}{e}\left(P_{\zeta}-mRv_{\zeta}\right)

Taking the Lagrangian derivative:

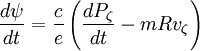
\frac{d\psi}{dt}= \frac{c}{e}\left(\frac{dP_{\zeta}}{dt}-mRv_{\zeta}\right)

Since Pζ is conserved, the first term is zero. Bounce averaging:

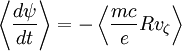
\left\langle \frac{d\psi}{dt}\right\rangle =-\left\langle \frac{mc}{e}Rv_{\zeta}\right\rangle

Since the particle returns to the same position and velocity after each bounce, 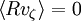\left\langle Rv_{\zeta}\right\rangle =0. Then:

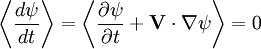
\left\langle \frac{d\psi}{dt}\right\rangle =\left\langle \frac{\partial\psi}{\partial t}+\mathbf{V}\cdot\nabla\psi\right\rangle =0

So that:

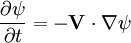
\frac{\partial\psi}{\partial t}=-\mathbf{V}\cdot\nabla\psi

Faraday's law is:

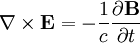
\nabla\times\mathbf{E}= -\frac{1}{c}\frac{\partial\mathbf{B}}{\partial t}

Writing \mathbf{B}=\nabla\times\mathbf{A}:

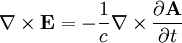
\nabla\times\mathbf{E}=-\frac{1}{c} \nabla\times\frac{\partial\mathbf{A}}{\partial t}

So:

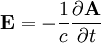
\mathbf{E}=-\frac{1}{c}\frac{\partial\mathbf{A}}{\partial t}

In the parallel direction:

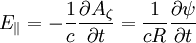
E_{\|}=-\frac{1}{c}\frac{\partial A_{\zeta}}{\partial t}=\frac{1}{cR}\frac{\partial\psi}{\partial t}

Plugging in:

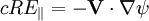
cRE_{\|}=-\mathbf{V}\cdot\nabla\psi

using Vr and 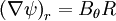\left(\nabla\psi\right)_{r}=B_{\theta}R:

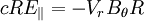
cRE_{\|}=-V_{r}B_{\theta}R

Or:

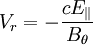
V_{r}=-\frac{cE_{\|}}{B_{\theta}}

This page was recovered in October 2009 from the Plasmagicians page on Generals_2003_II_2 dated 01:35, 10 May 2007.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Generals/2003_II_2"
Personal tools