2003 II 5
From QED
This diagram is the same as in White, for the bound-state problem.
By the Bohr-Sommerfeld condition, if we want the solution that goes
to zero at both 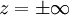 , we must have:
, we must have:
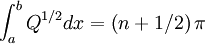
Then:
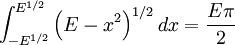
So that E = 2n + 1.
The solutions in region 1 are (using b = E1 / 2):
![\left(b,z\right)=\frac{1}{\left(E-z^{2}\right)^{1/4}}\exp\left[-i\int_{b}^{z}\left(E-x^{2}\right)^{1/2}dx\right]](../../../images/math/7/d/7/7d71259f0d06cca81156043f2922456a.png)
It is clear that this is unbounded, and is the dominant solution for z > b. Then to get the solution that is zero at z = a:
![y\left(z=a\right)=0=\frac{A}{\left(E-a^{2}\right)^{1/4}}\exp\left[-i\int_{b}^{a}\left(E-x^{2}\right)^{1/2}dx\right]+\frac{B}{\left(E-a^{2}\right)^{1/4}}\exp\left[i\int_{b}^{a}\left(E-x^{2}\right)^{1/2}dx\right]](../../../images/math/9/0/f/90f130dd43a183777828d82ace4e5a7f.png)
This relation can be simplified:
![\frac{A}{B}=-\exp\left[2i\int_{b}^{a}\left(E-x^{2}\right)^{1/2}dx\right]](../../../images/math/5/c/3/5c338a8f7a404626545edfc7d526dd7b.png)
Then:
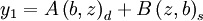
Crossing to region 2, we hop off the stokes line and so we pick up half of the stokes constant:
![y_{2}=A\left(b,z\right)_{d}+\left[B+\frac{i}{2}A\right]\left(z,b\right)_{s}](../../../images/math/5/a/7/5a7fa23b5f38aeeea102138863254046.png)
Then we cross an anti-stokes:
![y_{3}=A\left(b,z\right)_{s}+\left[B+\frac{i}{2}A\right]\left(z,b\right)_{d}](../../../images/math/d/8/e/d8eba41362c2b464fd8e63bee662e679.png)
Now we must cross a stokes:
![y_{4}=\left[\frac{1}{2}A+iB\right]\left(b,z\right)_{s}+\left[B+\frac{i}{2}A\right]\left(z,b\right)_{d}](../../../images/math/8/9/2/892fdb199fb493194ce655910c8ed526.png)
This will then be the solution on the axis. Now if we were to connect with the zero at − b:
![y_{5}=\left[\frac{1}{2}A+iB\right]\left[b,-b\right]\left(-b,z\right)_{s}+\left[B+\frac{i}{2}A\right]\left(z,-b\right)_{d}\left[-b,b\right]](../../../images/math/5/d/d/5ddd80f3439e901d740c59e8281caa81.png)
Using ![\left[-b,b\right]=\exp\left(-i\int_{-b}^{b}Q^{1/2}dz\right)=e^{-iW}](../../../images/math/3/3/0/330109aa6b4e605d456cdfb31060e264.png) :
:
![y_{5}=\left[\frac{1}{2}A+iB\right]e^{iW}\left(-b,z\right)_{s}+\left[B+\frac{i}{2}A\right]e^{-iW}\left(z,-b\right)_{d}](../../../images/math/e/e/0/ee055ff450e8fbf4e9abe0746c95ef36.png)
Now requiring that 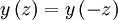 :
:
![\left[\frac{1}{2}A+iB\right]\left(b,z\right)_{s}+\left[B+\frac{i}{2}A\right]\left(z,b\right)_{d}=\left[\frac{1}{2}A+iB\right]e^{iW}\left(-b,-z\right)_{s}+\left[B+\frac{i}{2}A\right]e^{-iW}\left(-z,-b\right)_{d}](../../../images/math/e/b/8/eb8fad2e6df22fd7da71b0b7f72a4134.png)
Since Q1 / 2 is even, 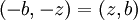 :
:
![\left[\frac{1}{2}A+iB\right]\left(b,z\right)+\left[B+\frac{i}{2}A\right]\left(z,b\right)=\left[\frac{1}{2}A+iB\right]e^{iW}\left(z,b\right)+\left[B+\frac{i}{2}A\right]e^{-iW}\left(b,z\right)](../../../images/math/f/2/0/f20ea1125ba5efb98e48e5d156b44e6b.png)
This gives an equation for W:
![B+\frac{i}{2}A=\left[\frac{1}{2}A+iB\right]e^{iW}](../../../images/math/c/9/c/c9cfaef7a801d073c0757f8c6e78781f.png)
Using the condition for A / B:
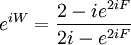
Where:
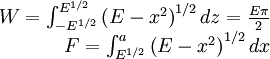
which will then give a condition on E. If 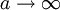 ,
,
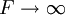 , and:
, and:
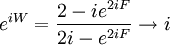
This will be satisfied if:
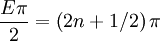
Or E = 4n + 1. This is different from part b because we have removed the odd solutions.
This page was recovered in October 2009 from the Plasmagicians page on Generals_2003_II_5 dated 01:13, 7 May 2007.












