Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

2003 I 2

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2003 I 2]])

Jump to: navigation, search

The radial electric field may be found by Poisson's equation:

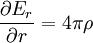
$\frac{\partial E_{r}}{\partial r}=4\pi\rho$

Since 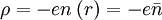$\rho=-en\left(r\right)=-e\bar{n}$ :

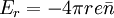
$E_{r}=-4\pi re\bar{n}$

The radial force balance is:

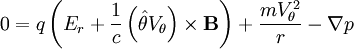
$0=q\left(E_{r}+\frac{1}{c}\left(\hat{\theta}V_{\theta}\right)\times\mathbf{B}\right)+\frac{mV_{\theta}^{2}}{r}-\nabla p$

Using $V θ = ω r r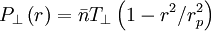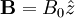$ , $P_{\perp}\left(r\right)=\bar{n}T_{\perp}\left(1-r^{2}/r_{p}^{2}\right)$ , $\mathbf{B}=B_{0}\hat{z}$ , and the result from part a:

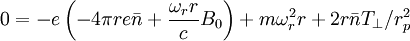
$0=-e\left(-4\pi re\bar{n}+\frac{\omega_{r}r}{c}B_{0}\right)+m\omega_{r}^{2}r+2r\bar{n}T_{\perp}/r_{p}^{2}$

Writing this in standard quadratic form:

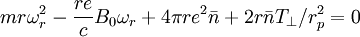
$mr\omega_{r}^{2}-\frac{re}{c}B_{0}\omega_{r}+4\pi re^{2}\bar{n}+2r\bar{n}T_{\perp}/r_{p}^{2}=0$

The quadratic formula gives:

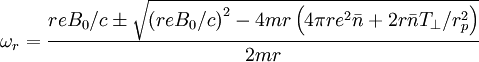
$\omega_{r}=\frac{reB_{0}/c\pm\sqrt{\left(reB_{0}/c\right)^{2}-4mr\left(4\pi re^{2}\bar{n}+2r\bar{n}T_{\perp}/r_{p}^{2}\right)}}{2mr}$

Rearranging:

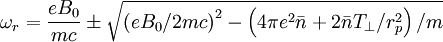
$\omega_{r}=\frac{eB_{0}}{mc}\pm\sqrt{\left(eB_{0}/2mc\right)^{2}-\left(4\pi e^{2}\bar{n}+2\bar{n}T_{\perp}/r_{p}^{2}\right)/m}$

Using $ω c = e B 0 / m c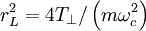$ , $r_{L}^{2}=4T_{\perp}/\left(m\omega_{c}^{2}\right)$ :

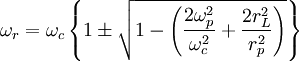
$\omega_{r}=\omega_{c}\left\{ 1\pm\sqrt{1-\left(\frac{2\omega_{p}^{2}}{\omega_{c}^{2}}+\frac{2r_{L}^{2}}{r_{p}^{2}}\right)}\right\}$

The maximum density that can be confined is where the $ω r$ becomes imaginary. Looking at eq. 2, this occurs at:

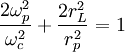
$\frac{2\omega_{p}^{2}}{\omega_{c}^{2}}+\frac{2r_{L}^{2}}{r_{p}^{2}}=1$

Plugging in for everything:

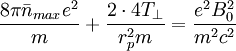
$\frac{8\pi\bar{n}_{max}e^{2}}{m}+\frac{2\cdot4T_{\perp}}{r_{p}^{2}m}=\frac{e^{2}B_{0}^{2}}{m^{2}c^{2}}$

Solving for 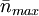$\bar{n}_{max}$ :

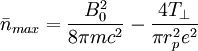
$\bar{n}_{max}=\frac{B_{0}^{2}}{8\pi mc^{2}}-\frac{4T_{\perp}}{\pi r_{p}^{2}e^{2}}$

For this value of 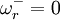$\omega_{r}^{-}=0$ .

The self-electric field energy is:

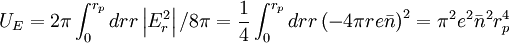
$U_{E}=2\pi\int_{0}^{r_{p}}drr\left|E_{r}^{2}\right|/8\pi=\frac{1}{4}\int_{0}^{r_{p}}drr\left(-4\pi re\bar{n}\right)^{2}=\pi^{2}e^{2}\bar{n}^{2}r_{p}^{4}$

Dividing by 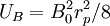$U_{B}=B_{0}^{2}r_{p}^{2}/8$ :

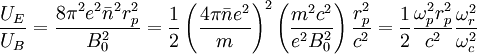
$\frac{U_{E}}{U_{B}}=\frac{8\pi^{2}e^{2}\bar{n}^{2}r_{p}^{2}}{B_{0}^{2}}=\frac{1}{2}\left(\frac{4\pi\bar{n}e^{2}}{m}\right)^{2}\left(\frac{m^{2}c^{2}}{e^{2}B_{0}^{2}}\right)\frac{r_{p}^{2}}{c^{2}}=\frac{1}{2}\frac{\omega_{p}^{2}r_{p}^{2}}{c^{2}}\frac{\omega_{r}^{2}}{\omega_{c}^{2}}$

The rotational kinetic energy is:

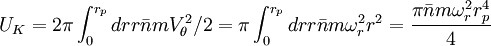
$U_{K}=2\pi\int_{0}^{r_{p}}drr\bar{n}mV_{\theta}^{2}/2=\pi\int_{0}^{r_{p}}drr\bar{n}m\omega_{r}^{2}r^{2}=\frac{\pi\bar{n}m\omega_{r}^{2}r_{p}^{4}}{4}$

Dividing by 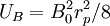$U_{B}=B_{0}^{2}r_{p}^{2}/8$ :

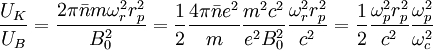
$\frac{U_{K}}{U_{B}}=\frac{2\pi\bar{n}m\omega_{r}^{2}r_{p}^{2}}{B_{0}^{2}}=\frac{1}{2}\frac{4\pi\bar{n}e^{2}}{m}\frac{m^{2}c^{2}}{e^{2}B_{0}^{2}}\frac{\omega_{r}^{2}r_{p}^{2}}{c^{2}}=\frac{1}{2}\frac{\omega_{p}^{2}r_{p}^{2}}{c^{2}}\frac{\omega_{p}^{2}}{\omega_{c}^{2}}$

This page was recovered in October 2009 from the Plasmagicians page on Generals_2003_I_2 dated 00:50, 7 May 2007.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Generals/2003_I_2"

Category: Plasma Physics Generals