Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

2003 I 3

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2003 I 3]])

Jump to: navigation, search

We have:

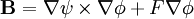
$\mathbf{B}=\nabla\psi\times\nabla\phi+F\nabla\phi$

The equilibrium equation is:

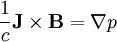
$\frac{1}{c}\mathbf{J}\times\mathbf{B}=\nabla p$

The first term is:

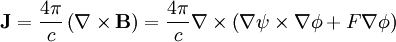
$\mathbf{J}=\frac{4\pi}{c}\left(\nabla\times\mathbf{B}\right)=\frac{4\pi}{c}\nabla\times\left(\nabla\psi\times\nabla\phi+F\nabla\phi\right)$

Simplifying:

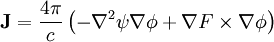
$\mathbf{J}=\frac{4\pi}{c}\left(-\nabla^{2}\psi\nabla\phi+\nabla F\times\nabla\phi\right)$

Then:

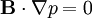
$\mathbf{B}\cdot\nabla p=0$

Plugging in:

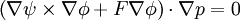
$\left(\nabla\psi\times\nabla\phi+F\nabla\phi\right)\cdot\nabla p=0$

Since the system is axisymmetric:

$\left(\nabla\psi\times\nabla\phi\right)\cdot\nabla p=\nabla\phi\cdot\left(\nabla\psi\times\nabla p\right)=0$

So that $p$ is only a function of $ψ$ . Then:

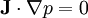
$\mathbf{J}\cdot\nabla p=0$

Giving:

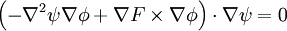
$\left(-\nabla^{2}\psi\nabla\phi+\nabla F\times\nabla\phi\right)\cdot\nabla\psi=0$

Since 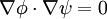$\nabla\phi\cdot\nabla\psi=0$ :

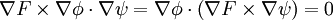
$\nabla F\times\nabla\phi\cdot\nabla\psi=\nabla\phi\cdot\left(\nabla F\times\nabla\psi\right)=0$

So that $F$ is a function of $ψ$ .

If we taylor expand $ψ$ :

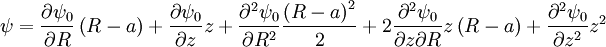
$\psi=\frac{\partial\psi_{0}}{\partial R}\left(R-a\right)+\frac{\partial\psi_{0}}{\partial z}z+\frac{\partial^{2}\psi_{0}}{\partial R^{2}}\frac{\left(R-a\right)^{2}}{2}+2\frac{\partial^{2}\psi_{0}}{\partial z\partial R}z\left(R-a\right)+\frac{\partial^{2}\psi_{0}}{\partial z^{2}}z^{2}$

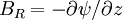The first order terms are just the magnetic field on axis ( $B_{z}=\partial\psi/\partial R$ , $B_{R}=-\partial\psi/\partial z$ ). If the flux surfaces are up-down symmetric, then the terms odd in $z$ must be zero. This gives:

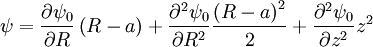
$\psi=\frac{\partial\psi_{0}}{\partial R}\left(R-a\right)+\frac{\partial^{2}\psi_{0}}{\partial R^{2}}\frac{\left(R-a\right)^{2}}{2}+\frac{\partial^{2}\psi_{0}}{\partial z^{2}}z^{2}$

So that the flux surfaces will be circular around the axis if 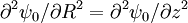$\partial^{2}\psi_{0}/\partial R^{2}=\partial^{2}\psi_{0}/\partial z^{2}$ .

The curvature of the field lines is just:

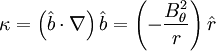
$\kappa=\left(\hat{b}\cdot\nabla\right)\hat{b}=\left(-\frac{B_{\theta}^{2}}{r}\right)\hat{r}$

This term describes the interaction of the pressure gradient and field line curvature. In cylindrical geometry, it will be:

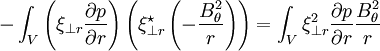
$-\int_{V}\left(\xi_{\perp r}\frac{\partial p}{\partial r}\right)\left(\xi_{\perp r}^{\star}\left(-\frac{B_{\theta}^{2}}{r}\right)\right)=\int_{V}\xi_{\perp r}^{2}\frac{\partial p}{\partial r}\frac{B_{\theta}^{2}}{r}$

This term will contribute to instability if 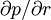$\partial p/\partial r$ is negative, since $δ W$ will be negative.