Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

2004 II 4

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2004 II 4]])

Jump to: navigation, search

This is a well-behaved function around $x = 0$ , so we write 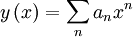$y\left(x\right)=\sum_{n}a_{n}x^{n}$ :

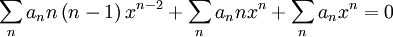
$\sum_{n}a_{n}n\left(n-1\right)x^{n-2}+\sum_{n}a_{n}nx^{n}+\sum_{n}a_{n}x^{n}=0$

Shifting the first by two:

$\sum_{n}\left[a_{n+2}\left(n+2\right)\left(n+1\right)+\left(n+1\right)a_{n}\right]x^{n}=0$

Then we get the recurrence relation:

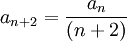
$a_{n+2}=\frac{a_{n}}{\left(n+2\right)}$

We get solutions for $a 0 = 0$ and $a 1 = 0$ :

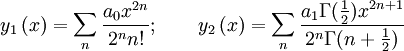
$y_{1}\left(x\right)=\sum_{n}\frac{a_{0}x^{2n}}{2^{n}n!};\qquad y_{2}\left(x\right)=\sum_{n}\frac{a_{1}\Gamma(\frac{1}{2})x^{2n+1}}{2^{n}\Gamma(n+\frac{1}{2})}$

The equation is:

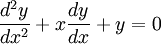
$\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}+y=0$

Using $y ˜ e S$ :

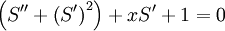
$\left(S^{\prime\prime}+\left(S^{\prime}\right)^{2}\right)+xS^{\prime}+1=0$

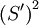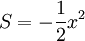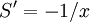Balance between $\left(S^{\prime}\right)^{2}$ , $S=-\frac{1}{2}x^{2}$ . There is an alternate balance between 1 and $S^{\prime}=-1/x$ , or $S = - log x$ . So the two asymptotic values are:

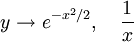
$y\rightarrow e^{-x^{2}/2},\quad \frac{1}{x}$

We use the integral:

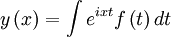
$y\left(x\right)=\int e^{ixt}f\left(t\right)dt$

Plugging in:

$\int\left[-t^{2}+xit+1\right]f\left(t\right)e^{ixt}dt=0$

Integrating by parts:

$\left.tf\left(t\right)e^{ixt}\right|_{C}-\int\left[t^{2}f\left(t\right)+tf^{\prime}\left(t\right)\right]e^{ixt}dt=0$

Solving this differential equation:

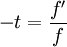
$-t=\frac{f^{\prime}}{f}$

Integrating:

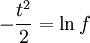
$-\frac{t^{2}}{2}=\ln f$

Or:

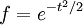
$f=e^{-t^{2}/2}$

Then the boundary becomes:

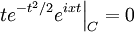
$\left.te^{-t^{2}/2}e^{ixt}\right|_{C}=0$

This goes to zero as 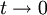$t\rightarrow0$ . So the Fourier-Laplace solutions are:

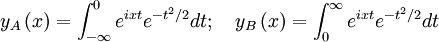
$y_{A}\left(x\right)=\int_{-\infty}^{0}e^{ixt}e^{-t^{2}/2}dt;\quad y_{B}\left(x\right)=\int_{0}^{\infty}e^{ixt}e^{-t^{2}/2}dt$

We can replace $t$ with $- t$ in $f A$ to get:

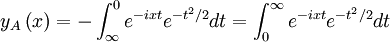
$y_{A}\left(x\right)=-\int_{\infty}^{0}e^{-ixt}e^{-t^{2}/2}dt=\int_{0}^{\infty}e^{-ixt}e^{-t^{2}/2}dt$

Then we can form:

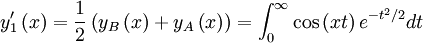
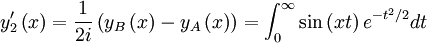
$y_{1}^{\prime}\left(x\right)=\frac{1}{2}\left(y_{B}\left(x\right)+y_{A}\left(x\right)\right)=\int_{0}^{\infty}\cos\left(xt\right)e^{-t^{2}/2}dt$ $y_{2}^{\prime}\left(x\right)=\frac{1}{2i}\left(y_{B}\left(x\right)-y_{A}\left(x\right)\right)=\int_{0}^{\infty}\sin\left(xt\right)e^{-t^{2}/2}dt$

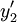$y_{2}^{\prime}$ is even and corresponds to $y 2$ .