2004 II 5

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2004 II 5]])
Jump to: navigation, search

Warning: this solution is wrong.

One's physical intuition should say that this problem will be self-similar of the child-langmuir problem, so that it is as if at some position − x0 there is an electrode emitting zero velocity ions at a higher potential (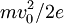mv_{0}^{2}/2e)

The electric field may be written as E = − dφ / dx. Then the 1D Poisson equation becomes:

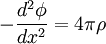
-\frac{d^{2}\phi}{dx^{2}}=4\pi\rho

Where ρ is the charge density. The current is:

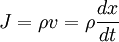
J=\rho v=\rho\frac{dx}{dt}

From the Lorentz force:

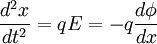
\frac{d^{2}x}{dt^{2}}=qE=-q\frac{d\phi}{dx}

Multiplying both sides by dx / dt:

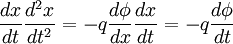
\frac{dx}{dt}\frac{d^{2}x}{dt^{2}}=-q\frac{d\phi}{dx}\frac{dx}{dt}=-q\frac{d\phi}{dt}

Integrating in time:

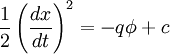
\frac{1}{2}\left(\frac{dx}{dt}\right)^{2}=-q\phi+c

Since we know that φ = 0 at x = 0, and v = v0, so we can determine c:

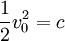
\frac{1}{2}v_{0}^{2}=c

Using the current equation to solve for ρ:

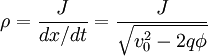
\rho=\frac{J}{dx/dt}=\frac{J}{\sqrt{v_{0}^{2}-2q\phi}}

Plugging in to Poisson's equation:

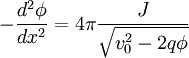
-\frac{d^{2}\phi}{dx^{2}}=4\pi\frac{J}{\sqrt{v_{0}^{2}-2q\phi}}

Multiplying by dφ / dx and integrating:

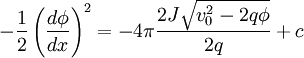
-\frac{1}{2}\left(\frac{d\phi}{dx}\right)^{2}=-4\pi\frac{2J\sqrt{v_{0}^{2}-2q\phi}}{2q}+c

Where we have another constant. Simplifying:

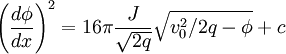
\left(\frac{d\phi}{dx}\right)^{2}=16\pi\frac{J}{\sqrt{2q}}\sqrt{v_{0}^{2}/2q-\phi}+c

The last constant may be found by setting φ = − φ0 at x = L. and integrating from φ = 0 at x = 0.

Since we are space-charge limited, the point where the velocity is zero should have zero electric field. If another ion entered, it would tip the field into the other direction and reflect any other particles. If the field were nonzero, more ions could enter the system (it is not a maximum).

Setting β = 0:

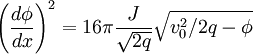
\left(\frac{d\phi}{dx}\right)^{2}=16\pi\frac{J}{\sqrt{2q}}\sqrt{v_{0}^{2}/2q-\phi}

This means:

\frac{d\phi}{dx}\left[v_{0}^{2}/2q-\phi\right]^{-1/4}=\left[16\pi\frac{J}{\sqrt{2q}}\right]^{1/2}

Integrating with respect to x:

-\frac{4}{3}\left[v_{0}^{2}/2q-\phi\right]^{3/4}=\left[16\pi\frac{J}{\sqrt{2q}}\right]^{1/2}x+c

Boundary conditions at x = 0 give 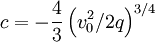c=-\frac{4}{3}\left(v_{0}^{2}/2q\right)^{3/4}. Then at φ = − φ0, x = L:

\frac{\sqrt{2q}}{16\pi L^{2}}\left[\frac{4}{3}\left(v_{0}^{2}/2q\right)^{3/4}-\frac{4}{3}\left(v_{0}^{2}/2q+\phi_{0}\right)^{3/4}\right]^{2}=J

We can simplify a little:

J=\frac{1}{9\pi L^{2}\left(2q\right)}\left[\left(v_{0}^{2}+2q\phi_{0}\right)^{3/2}-v_{0}^{3/2}\right]^{2}

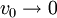As v_{0}\rightarrow0:

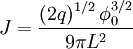
J=\frac{\left(2q\right)^{1/2}\phi_{0}^{3/2}}{9\pi L^{2}}

This page was recovered in October 2009 from the Plasmagicians page on Generals_2004_II_5 dated 22:30, 9 May 2007.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Generals/2004_II_5"
Personal tools