Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

2004 I 6

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2004 I 6]])

Jump to: navigation, search

$δ W$ is given as:

$\delta W=\frac{1}{2}\int_{V}\left[\gamma p\left|\nabla\cdot\xi\right|^{2}-\xi^{\star}\cdot\nabla\left(\xi\cdot\nabla p\right)+\left|Q\right|^{2}/\mu-\xi^{\star}\cdot\mathbf{j}\times\mathbf{Q}\right]d^{3}x$

The MHD equations are:

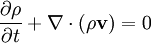
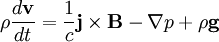
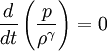
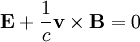
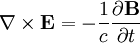
$\frac{\partial\rho}{\partial t}+\nabla\cdot\left(\rho\mathbf{v}\right)=0$ $\rho\frac{d\mathbf{v}}{dt}=\frac{1}{c}\mathbf{j}\times\mathbf{B}-\nabla p+\rho\mathbf{g}$ $\frac{d}{dt}\left(\frac{p}{\rho^{\gamma}}\right)=0$ $\mathbf{E}+\frac{1}{c}\mathbf{v}\times\mathbf{B}=0$ $\nabla\times\mathbf{E}=-\frac{1}{c}\frac{\partial\mathbf{B}}{\partial t}$

The linearized equations are:

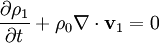
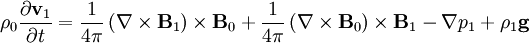
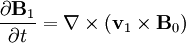
$\frac{\partial\rho_{1}}{\partial t}+\rho_{0}\nabla\cdot\mathbf{v}_{1}=0$ $\rho_{0}\frac{\partial\mathbf{v}_{1}}{\partial t}=\frac{1}{4\pi}\left(\nabla\times\mathbf{B}_{1}\right)\times\mathbf{B}_{0}+\frac{1}{4\pi}\left(\nabla\times\mathbf{B}_{0}\right)\times\mathbf{B}_{1}-\nabla p_{1}+\rho_{1}\mathbf{g}$ $\frac{\partial\mathbf{B}_{1}}{\partial t}=\nabla\times\left(\mathbf{v}_{1}\times\mathbf{B}_{0}\right)$ $\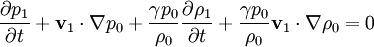frac{\partial p_{1}}{\partial t}+\mathbf{v}_{1}\cdot\nabla p_{0}+ \frac{\gamma p_{0}}{\rho_{0}}\frac{\partial\rho_{1}}{\partial t}+ \frac{\gamma p_{0}}{\rho_{0}}\mathbf{v}_1\cdot \nabla \rho_0 =0$

We can combine the first and fourth equations:

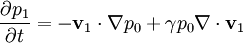
$\frac{\partial p_{1}}{\partial t}=-\mathbf{v}_{1}\cdot\nabla p_{0}+\gamma p_{0}\nabla\cdot\mathbf{v}_{1}$

For displacement $ξ$ , the equations become:

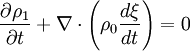
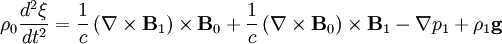
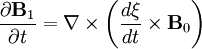
$\frac{\partial\rho_{1}}{\partial t}+\nabla\cdot\left(\rho_{0}\frac{d\xi}{dt}\right)=0$ $\rho_{0}\frac{d^{2}\xi}{dt^{2}}=\frac{1}{c}\left(\nabla\times\mathbf{B}_{1}\right)\times\mathbf{B}_{0}+\frac{1}{c}\left(\nabla\times\mathbf{B}_{0}\right)\times\mathbf{B}_{1}-\nabla p_{1}+\rho_{1}\mathbf{g}$ $\frac{\partial\mathbf{B}_{1}}{\partial t}=\nabla\times\left(\frac{d\xi}{dt}\times\mathbf{B}_{0}\right)$ $\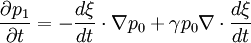frac{\partial p_{1}}{\partial t}=-\frac{d\xi}{dt}\cdot\nabla p_{0}+\gamma p_{0}\nabla\cdot\frac{d\xi}{dt}$

Integrating in time:

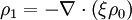
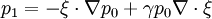
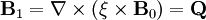
$\rho_{1}=-\nabla\cdot\left(\xi\rho_{0}\right)$ $p_{1}=-\xi\cdot\nabla p_{0}+\gamma p_{0}\nabla\cdot\xi$ $\mathbf{B}_{1}=\nabla\times\left(\xi\times\mathbf{B}_{0}\right)=\mathbf{Q}$

So the momentum equation becomes:

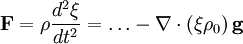
$\mathbf{F}=\rho\frac{d^{2}\xi}{dt^{2}}=\ldots-\nabla\cdot\left(\xi\rho_{0}\right)\mathbf{g}$

And the potential energy becomes:

$\delta W=-\frac{1}{2}\int\xi^{\star}\cdot\mathbf{F}d\mathbf{r}=\frac{1}{2}\int \left[\ldots +\rho_{0}\left(\xi^{\star}\cdot\mathbf{g}\right)\left(\nabla\cdot\xi\right) +\left(\xi^{\star}\cdot\mathbf{g}\right)\left(\xi\cdot \nabla \rho_0\right) \right]d\mathbf{r}$

This page was recovered in October 2009 from the Plasmagicians page on Generals_2004_I_6 dated 21:30, 11 May 2007.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Generals/2004_I_6"

Category: Plasma Physics Generals